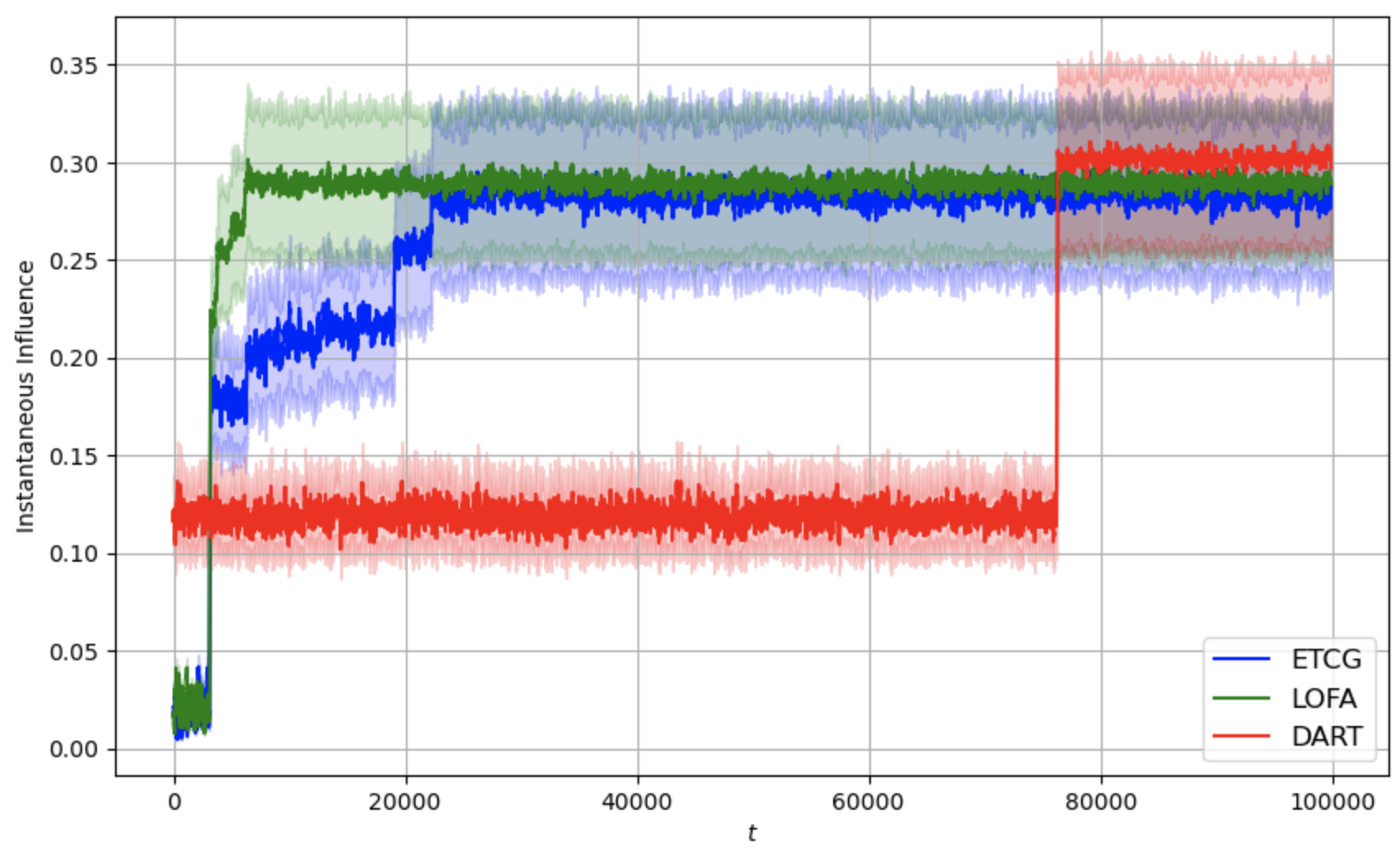
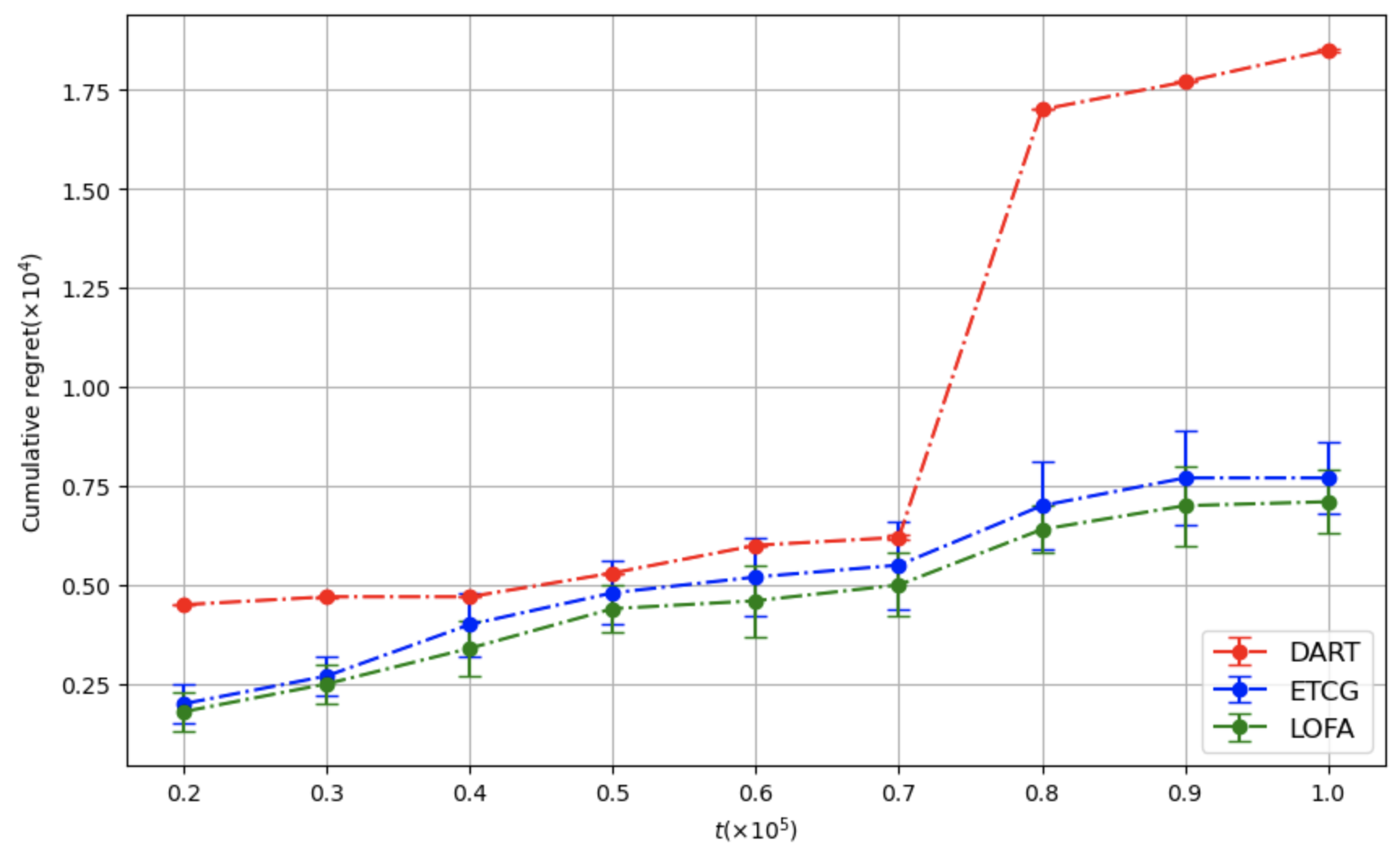
We study the problem of influence maximization (IM) in an online setting, where the goal is to select a subset of nodes-called the seed set-at each time step over a fixed time horizon, subject to a cardinality budget constraint, to maximize the expected cumulative influence. We operate under a full-bandit feedback model, where only the influence of the chosen seed set at each time step is observed, with no additional structural information about the network or diffusion process. It is well-established that the influence function is submodular, and existing algorithms exploit this property to achieve low regret. In this work, we leverage this property further and propose the Lazy Online Forward Algorithm (LOFA), which achieves a lower empirical regret. We conduct experiments on a real-world social network to demonstrate that LOFA achieves superior performance compared to existing bandit algorithms in terms of cumulative regret and instantaneous reward.
The Influence Maximization (IM) problem is a fundamental challenge in social network analysis that aims to identify a small set of influential nodes (seed users) in a network such that their activation leads to the maximum spread of influence (David et al. 2003). This problem has significant applications in various domains, such as viral marketing, social network analysis, rumor control, and public health campaigns, where understanding and leveraging network dynamics are crucial. Companies seek to leverage network effects to promote products through word-of-mouth marketing, while policymakers aim to maximize the reach of awareness campaigns with minimal resources. Influence Maximization helps optimize these processes by selecting the most effective set of influencers.
The IM problem can be categorized into offline and online settings based on network knowledge and the decision-making process. Some IM research primarily focuses on an offline setting, where the entire network structure and influence probabilities are known in advance, allowing for precomputation of optimal seed sets. However, in real-world scenarios, networks often evolve dynamically, and influence propagation occurs in real-time, necessitating the study of IM in an online setting.
Our research focuses on the online IM problem, where decisions must be made adaptively as the network changes or new information becomes available.
IM has been extensively studied in different settings. We briefly survey some representative work as follows. Kempe et al. (2003) introduced the foundational IM framework under the Independent Cascade (IC) and Linear Threshold (LT) models, proving submodularity of the influence function and enabling a greedy algorithm (Nemhauser et al. 1978) with (1 -1/e) approximation. Leskovec et al. (2007) proposed the Cost-Effective Lazy Forward (CELF) algorithm, enhancing greedy efficiency via submodularity, which is further improved by Goyal et al. (2011b) as CELF++. Christian et al. (2012) improved the offline scalability using Reverse Influence Sampling (RIS), now central to many offline IM algorithms, although it is limited for online settings. Recently, community-based methods (Umrawal and Aggarwal 2023, Umrawal et al. 2023b, Robson and Umrawal 2025) have also been explored to improve the runtime further.
Next, the Combinatorial Multi-Armed Bandit (CMAB) approaches adapt Upper Confidence Bound (UCB) (Alexandra et al. 2015), Thompson Sampling (Daniel and Benjamin 2016), and related strategies to submodular rewards, with regret bounds established under semi-and fullbandit feedback (Streeter andGolovin 2008, Niazadeh et al. 2021). Nie et al. (2022) proposed Explore-Then-Commit Greedy for stochastic submodular rewards with full-bandit feedback, while Agostinho and Jose (2024) introduced ClusterGreedy under LT by partitioning nodes. Qi and Feng (2023) applied the Moth-Flame Optimization Algorithm for influencer identification, and Chen et al. (2016) developed Combinatorial UCB (CUCB) for probabilistically triggered arms. Furthermore, Online IM research addresses dynamic networks and partial feedback. Yixin et al. (2016) proposed adaptive seed selection with heuristic methods, while Lichao et al. (2018) used a CMAB framework to balance exploration and exploitation under limited feedback, though computationally intensive. In addition, we survey methods for general non-linear reward functions beyond submodularity, such as CMAB-SM (Agarwal et al. 2021a(Agarwal et al. , 2022)), a divide-and-conquer strategy to efficiently handle large action spaces, and DART (Agarwal et al. 2021b), a successive accept-reject algorithm.
All these studies illustrate the evolution of IM from static offline methods like RIS to online adaptive approaches. Our work focuses on bridging efficiency and adaptability in online IM while maintaining a competitive regret.
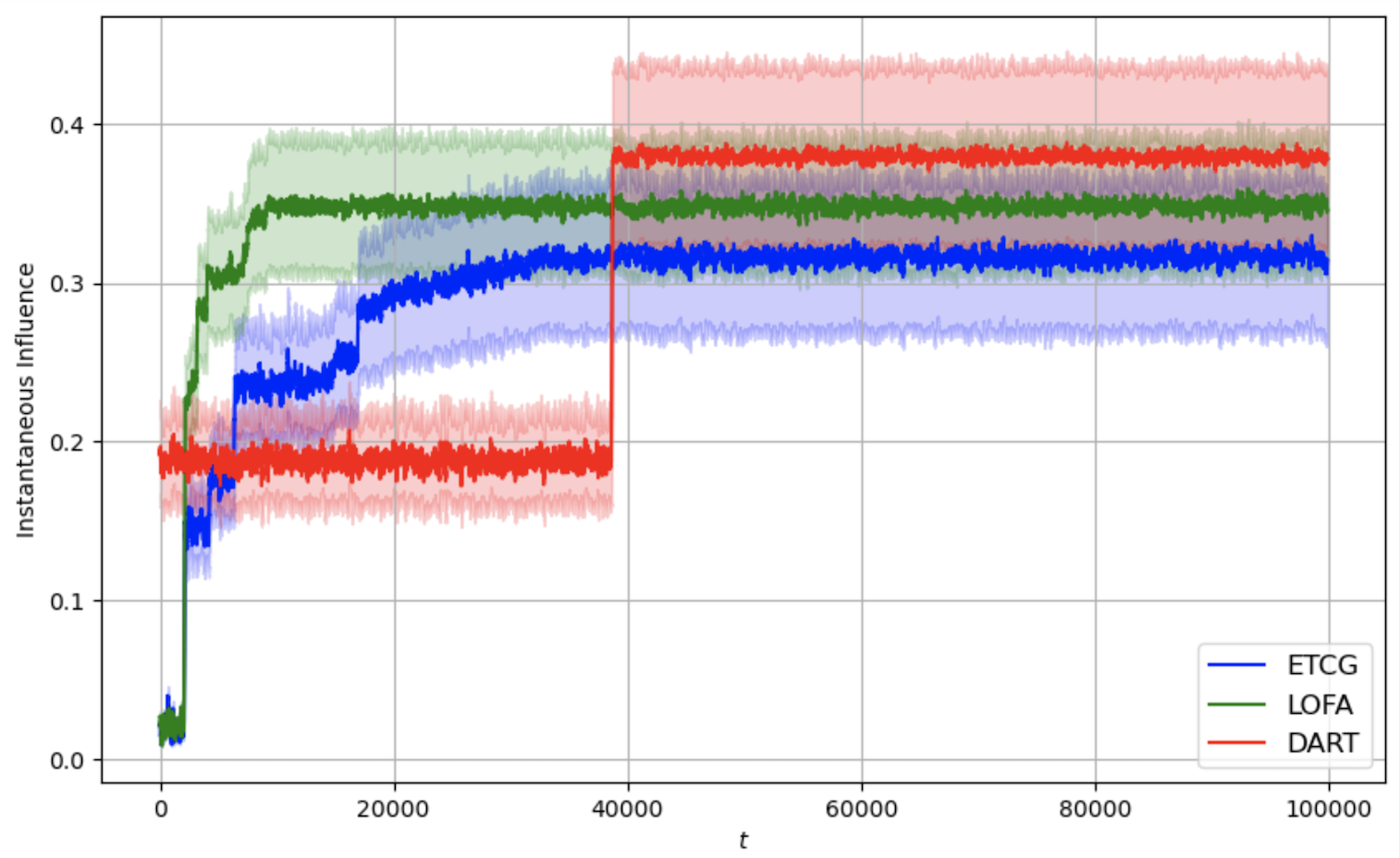
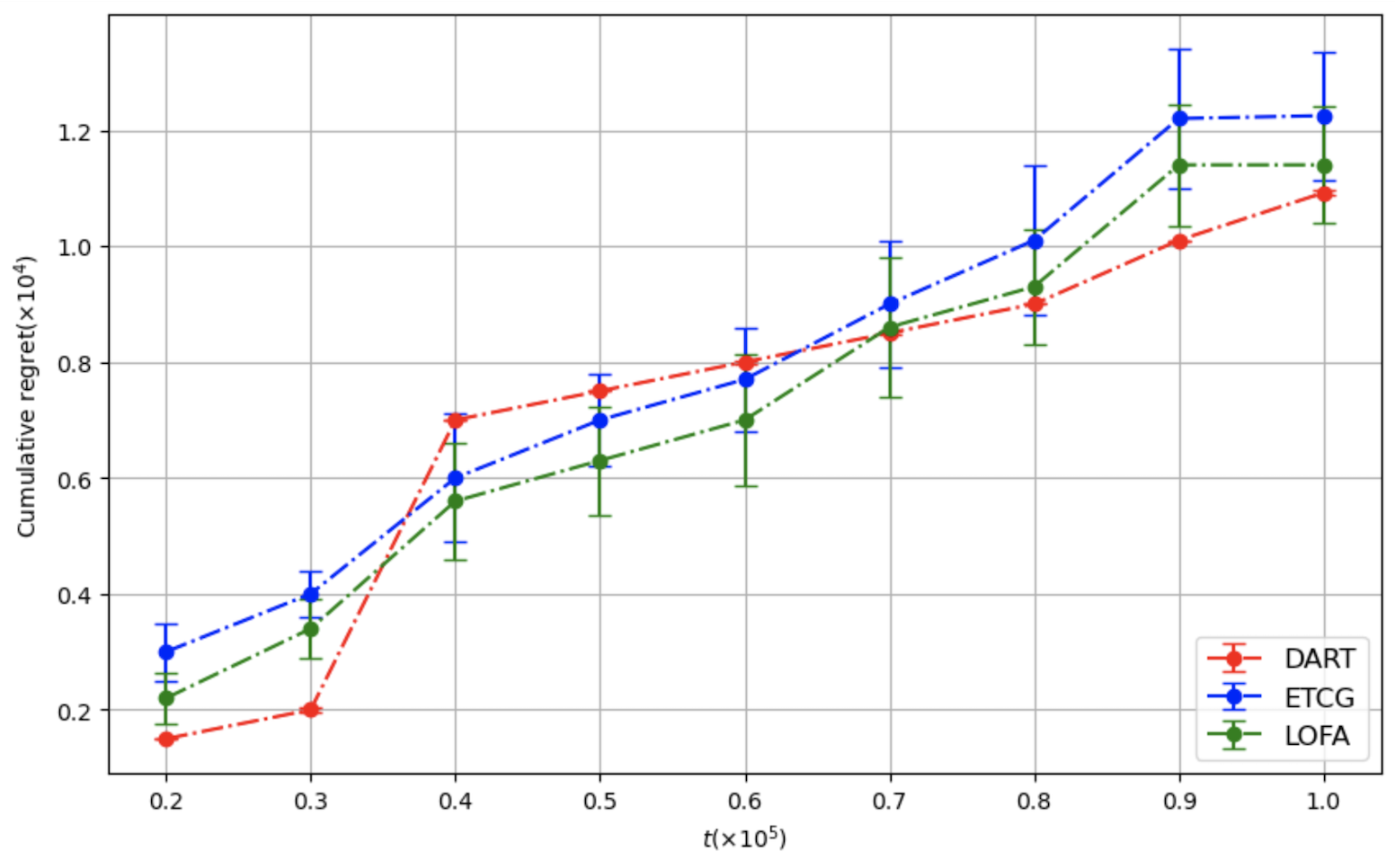
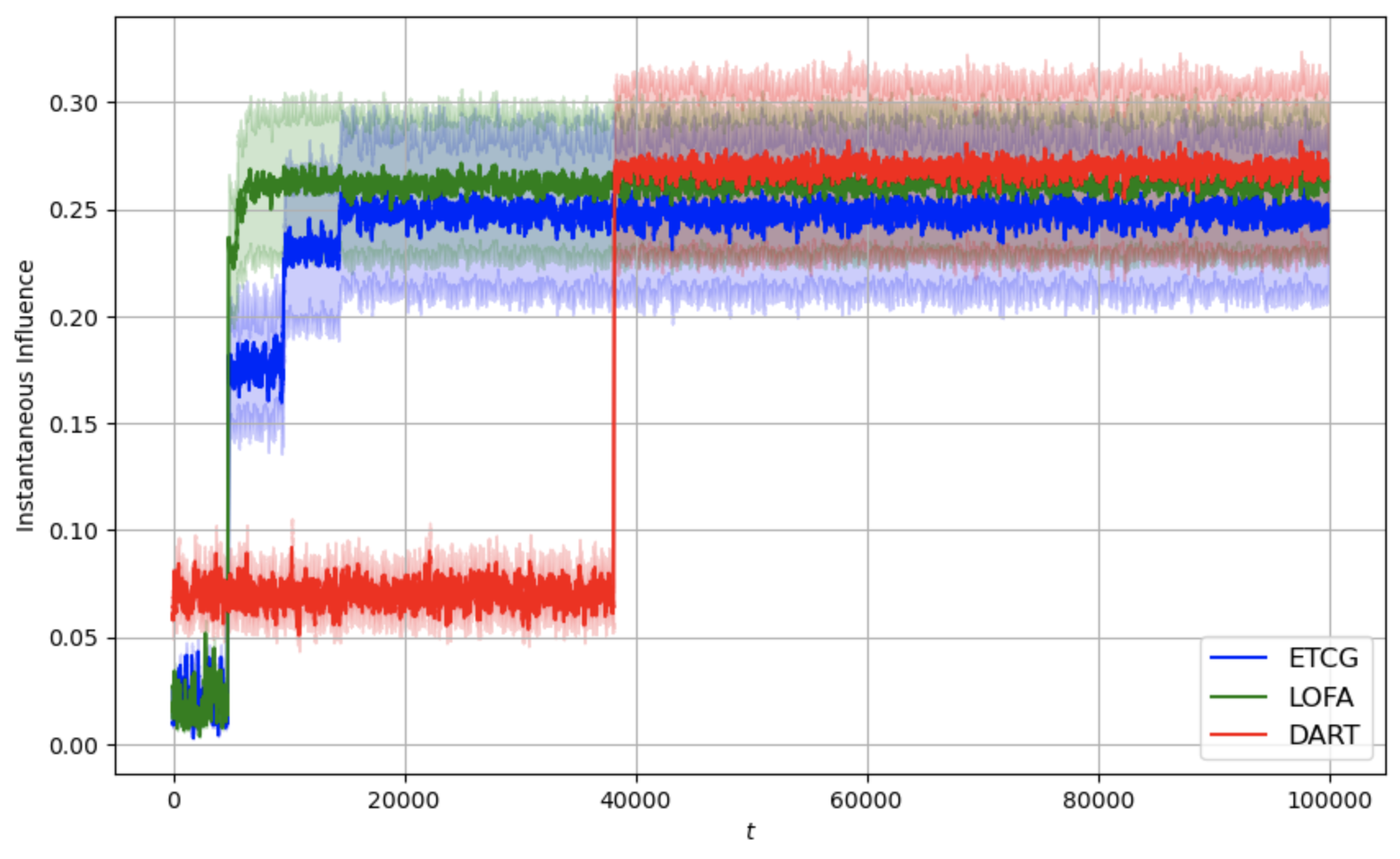
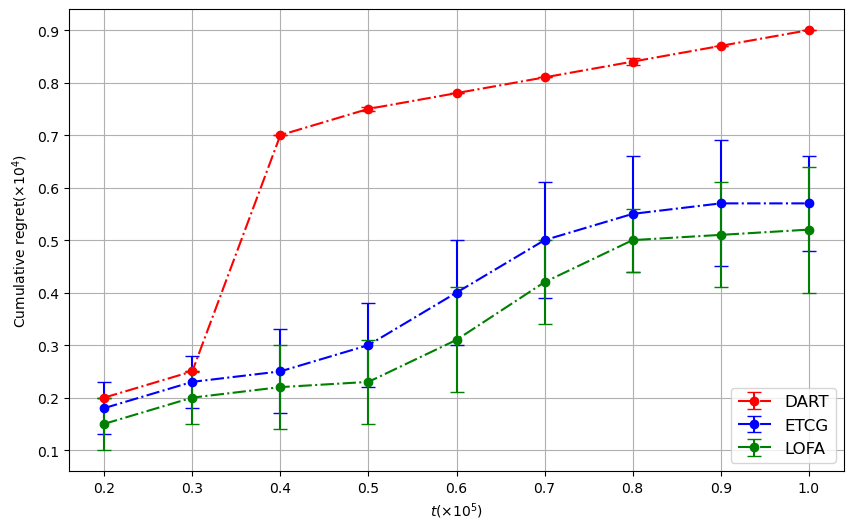
We propose the Lazy Online Forward Algorithm (LOFA) for the Influence Maximization (IM) problem in an online setting under full-bandit feedback. Using experiments on a real-world social network, we show that LOFA outperforms other methods in terms of empirical reward and regret.
The rest of the paper is structured as follows. Section 2 provides preliminaries and formulates the problem of interest. Section 3 discusses the proposed Online Lazy Forward Algorithm (LOFA).
Section 4 demonstrates the implementation of LOFA on a real-world social network against competing baselines and shows its superior performance. Section 5 concludes the paper and provides some future directions.
The Online Influence Maximization (IM) Problem is an extension of the classical IM problem, where the goal is to sequentially select a set of seed nodes in a social network to maximize the expected spread of influence over time. In this section, we discuss some preliminaries and formulate the problem of interest in this paper. Let Ω denote the ground set of n elements. A function:
Diffusion models describe the process
This content is AI-processed based on open access ArXiv data.