The presence of outliers in Large Language Models (LLMs) weights and activations makes them difficult to quantize. Recent work has leveraged rotations to mitigate these outliers. In this work, we propose methods that learn fusible rotations by minimizing principled and cheap proxy objectives to the weight quantization error. We primarily focus on GPTQ as the quantization method. Our main method is OptRot, which reduces weight outliers simply by minimizing the element-wise fourth power of the rotated weights. We show that OptRot outperforms both Hadamard rotations and more expensive, data-dependent methods like SpinQuant and OSTQuant for weight quantization. It also improves activation quantization in the W4A8 setting. We also propose a data-dependent method, OptRot + , that further improves performance by incorporating information on the activation covariance. In the W4A4 setting, we see that both OptRot and OptRot + perform worse, highlighting a trade-off between weight and activation quantization.
Increasing model size has enabled LLMs to perform a range of tasks (Achiam et al., 2023;Grattafiori et al., 2024;Yang et al., 2025), encouraging practitioners to design huge models with billions of parameters. Post Training Quantization (PTQ) is a widely adopted strategy for compressing these models by lowering their precision, while limiting the drop in performance to enable efficient inference (Xu et al., 2024). Scalar quantization is the most popular PTQ approach and relies on mapping each parameter value to a point on a finite precision grid, determined by the bit-width. Outliers prevent the finite grid from uniformly covering all values and can lead to large quantization errors. Hence, outlier reduction has increasingly received attention as a crucial pre-processing step (Chee et al., 2023) for PTQ with algorithms like simple Round-to-Nearest (RTN) or the more powerful GPTQ (Frantar et al., 2022).
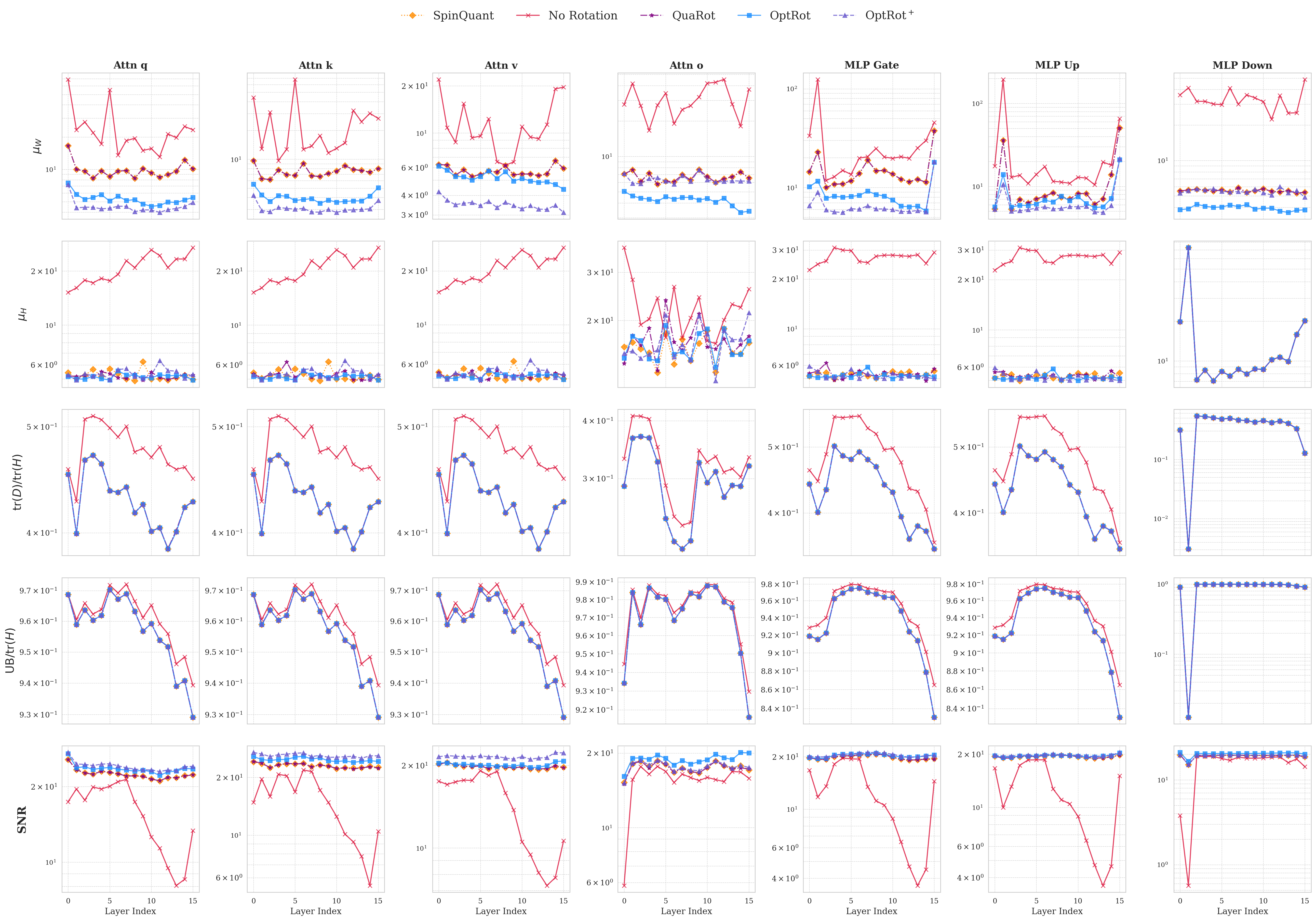
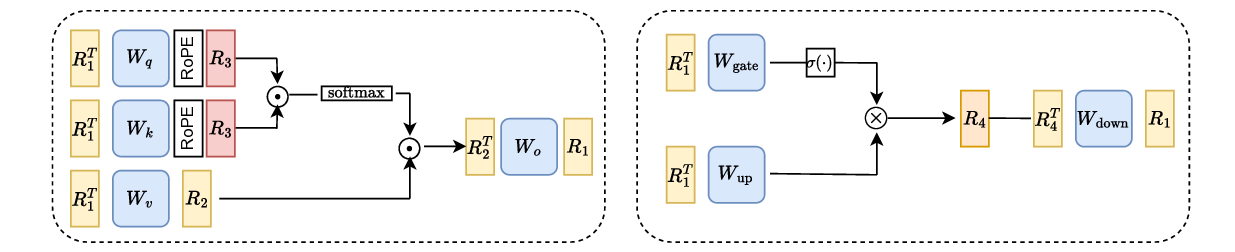
Recent work has applied rotations to weight matrices to mitigate outliers in weights and activations while keeping the network functionally equivalent. Hadamard rotations have shown to significantly improve the performance of GPTQ (Ashkboos et al., 2024;Tseng et al., 2024). To minimize overhead, these rotations can be materialized online efficiently with the Walsh-Hadamard transform, and in some cases they can also be fused with model weights. Fused rotations can also be learned without increasing inference cost. Learning rotations significantly improves performance. Heuristics like making the weight or activation distribution more uniform (Akhondzadeh et al., 2025;Shao et al., 2025) have shown to learn better rotations. Further improvements have been achieved by minimizing the loss of the model when rotated and then quantized in the forward pass (Liu et al., 2024). However, this quantization-aware training phase uses exclusively RTN as the quantization method, since GPTQ would be too slow.
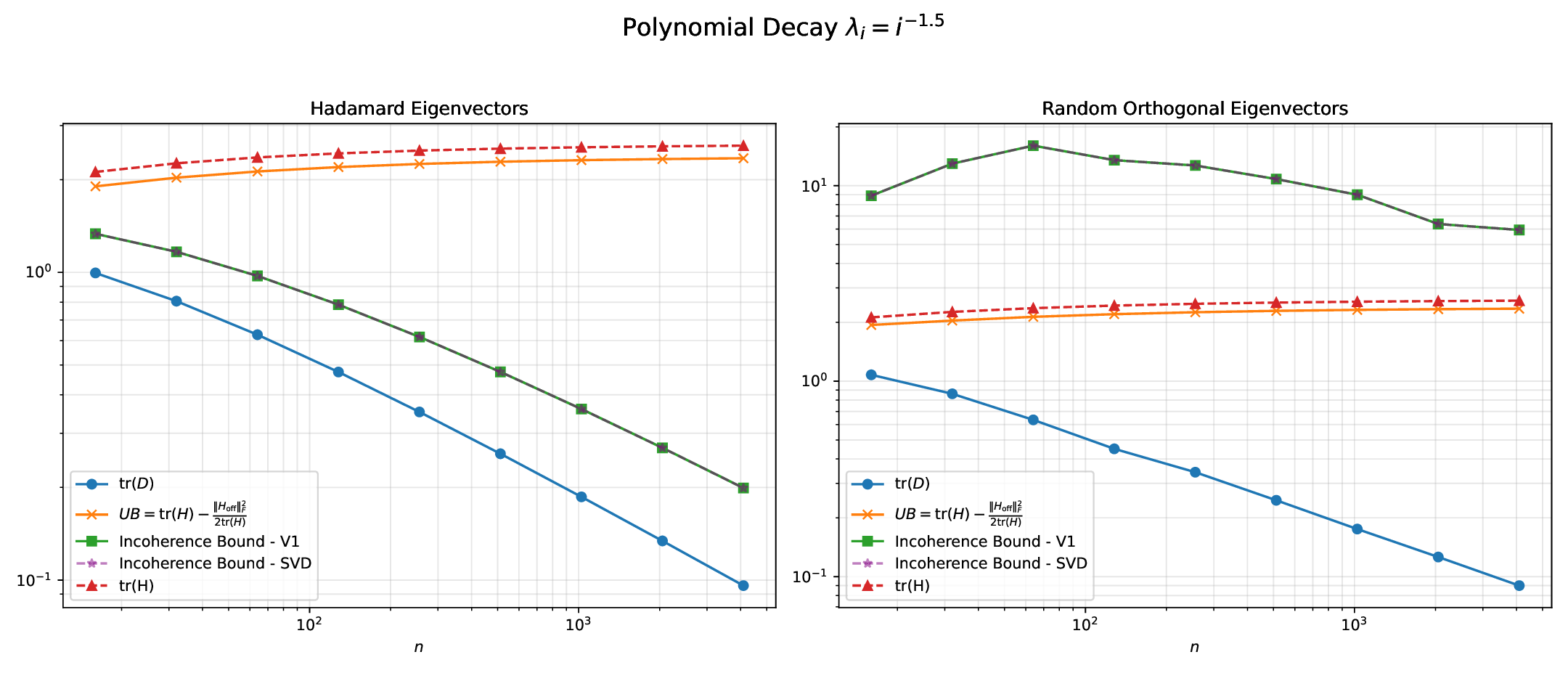
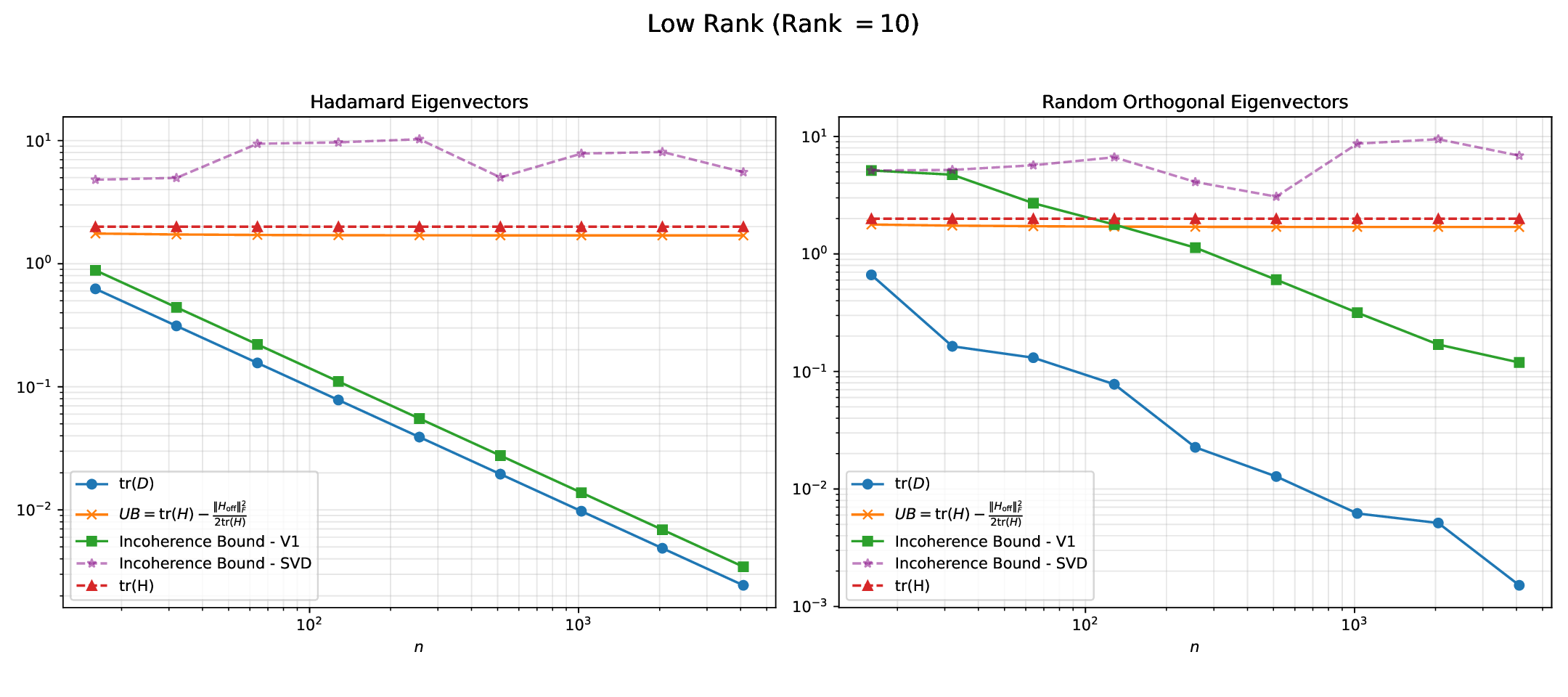
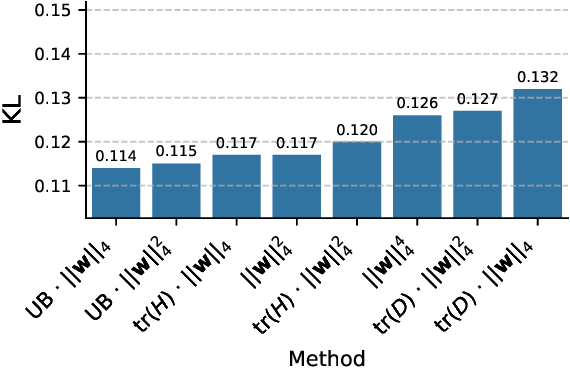
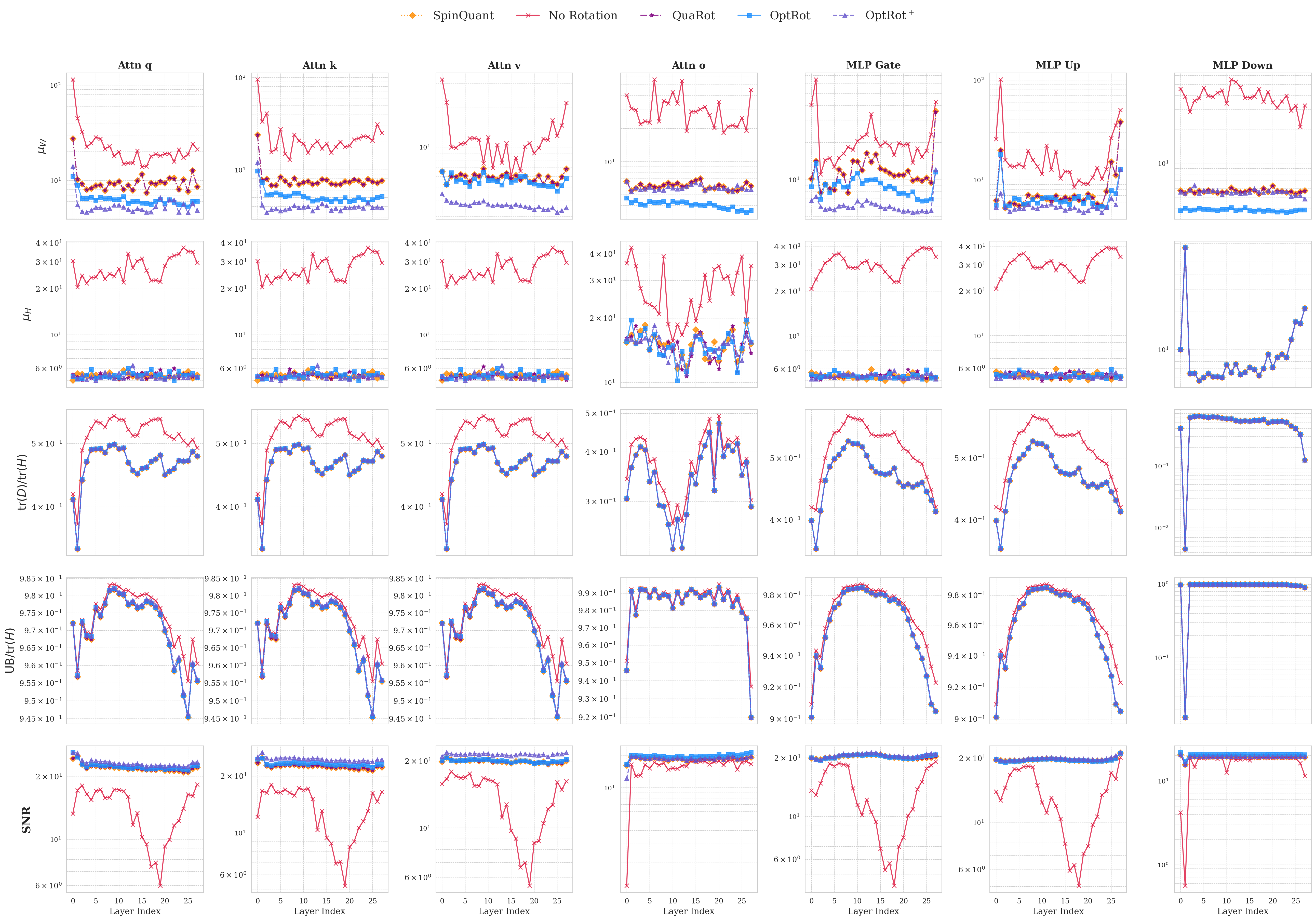
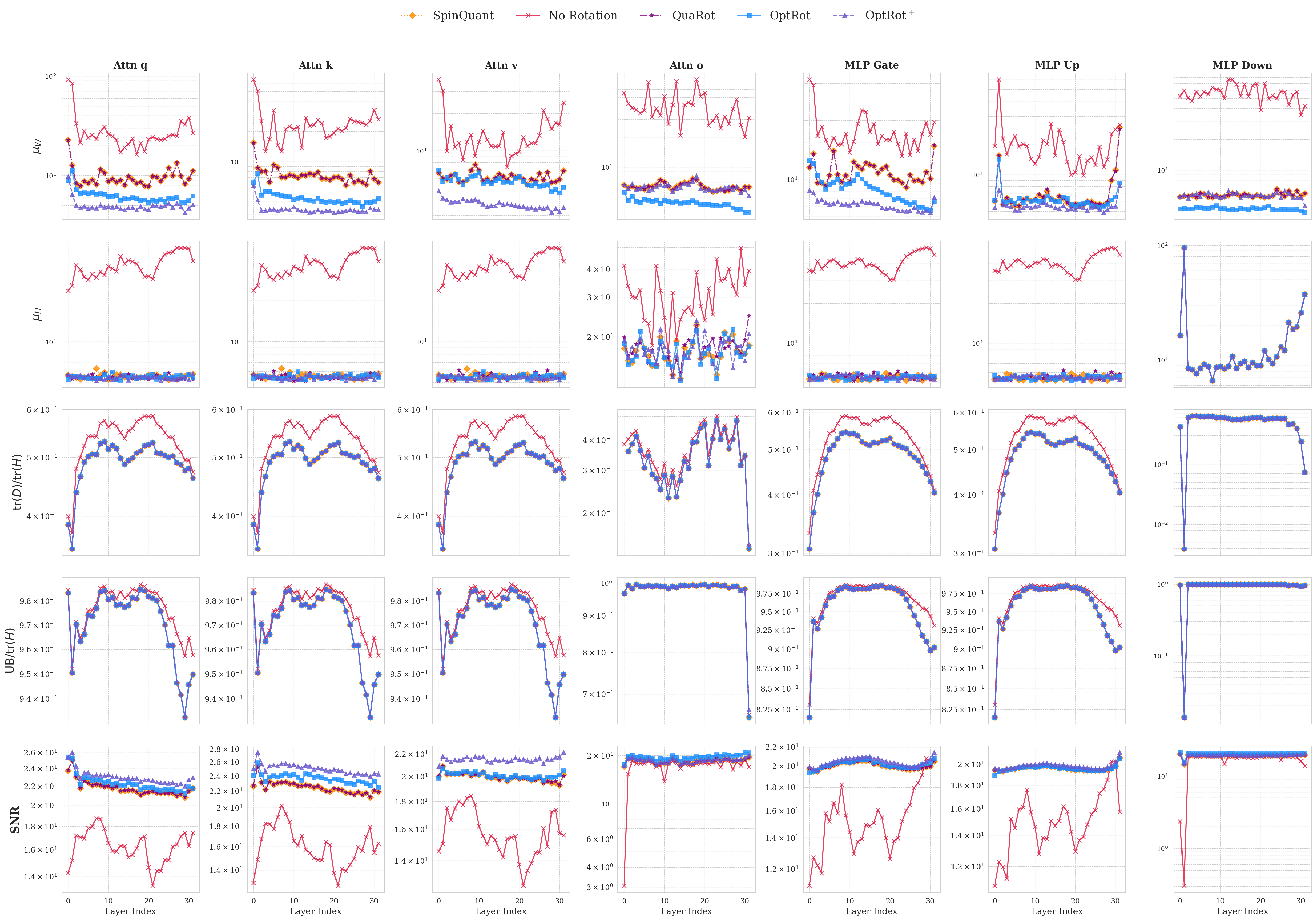
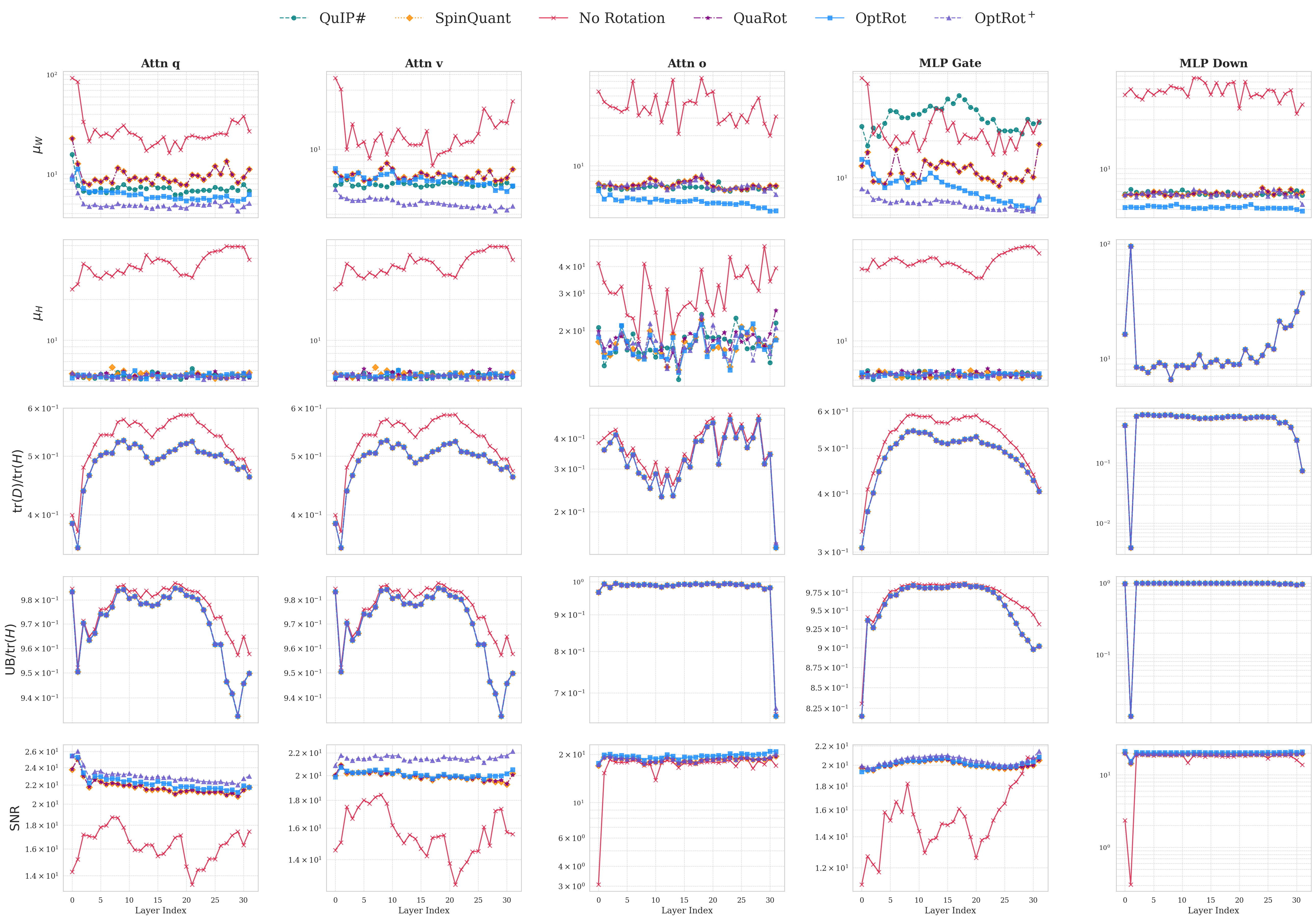
In this paper, we design efficient objectives to learn rotations that provably improve the quantization error, without quantization-aware training. To do so, we closely examine the GPTQ quantization objective, which minimizes a layerwise approximation of the KL divergence between the quantized and original model. A smaller KL divergence, implies better quantization -the quantized model is closer to the original. Leveraging the theoretical framework proposed by Chee et al. (2023), we show that the GPTQ objective has an upper bound which depends on the weight incoherence (which captures the degree of weight outliers).
We propose OptRot, a data-free method that learns rotations by minimizing a smooth proxy for the weight incoherence of the model: the element-wise fourth power of the rotated weights. We show that OptRot achieves better incoherence and weight quantization performance than QuaRot, Spin-Quant, OSTQuant and QuIP#. Different to prior work, Op-tRot is data-free and (except Kurtail) quantization-agnostic: it does not require a calibration set or the quantization scheme to learn rotations. OptRot can also learn rotations OptRot by optimizing a subset of the weights, without loading the entire model on GPU.
We also derive an upper bound to the GPTQ error that, in addition to the weight incoherence, also depends on a quantity related to the amount of feature correlation captured by the covariance matrix of the activations (or Hessian), which can be changed via rotations. Higher feature correlations makes quantizing with GPTQ easier. To this end, we introduce OptRot + , a data-dependent extension of OptRot, which learns rotations that jointly optimize the weight incoherence and Hessian feature correlation. OptRot + trades off data independence for smaller KL divergence of the quantized model.
Our contributions can be summarized as follows:
• We derive cheap proxy objectives to learn rotations that improve weight quantization error. We do so by extending the theoretical framework of Chee et al. (2023) and deriving error bounds for quantization with GPTQ and round-to-nearest (RTN).
• We propose OptRot, a data-free method which learns rotations that reduces the weight incoherence by minimizing the elementwise fourth power of weights. We also propose a data-dependent version, OptRot + , that further improves performance.
• OptRot outperforms methods like SpinQuant, QuaRot and OSTQuant for weight-only quantization and is competetive with SpinQuant for activation quantization with A8W4. We also observe a trade-off for activation quantization with A4W4, where reducing weight incoherence worsens activation quantization.
GPTQ (Frantar et al., 2022) is the most commonly used scalar quantization method for weight quantization, strongly outperforming the round-to-nearest (RTN) baseline. Outliers, present in weights and activations can significantly impact the quantization performance of GPTQ (and RTN).
Various approaches have tried to tackle outliers in this regard. Dettmers et al. (2022) suggest a mixed precision method w
This content is AI-processed based on open access ArXiv data.