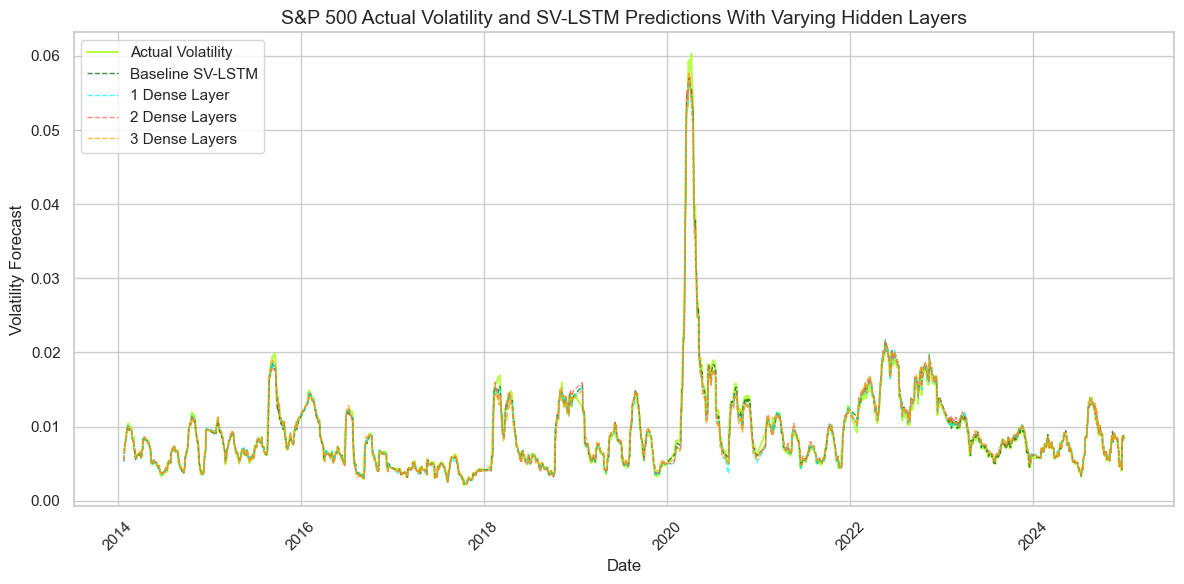
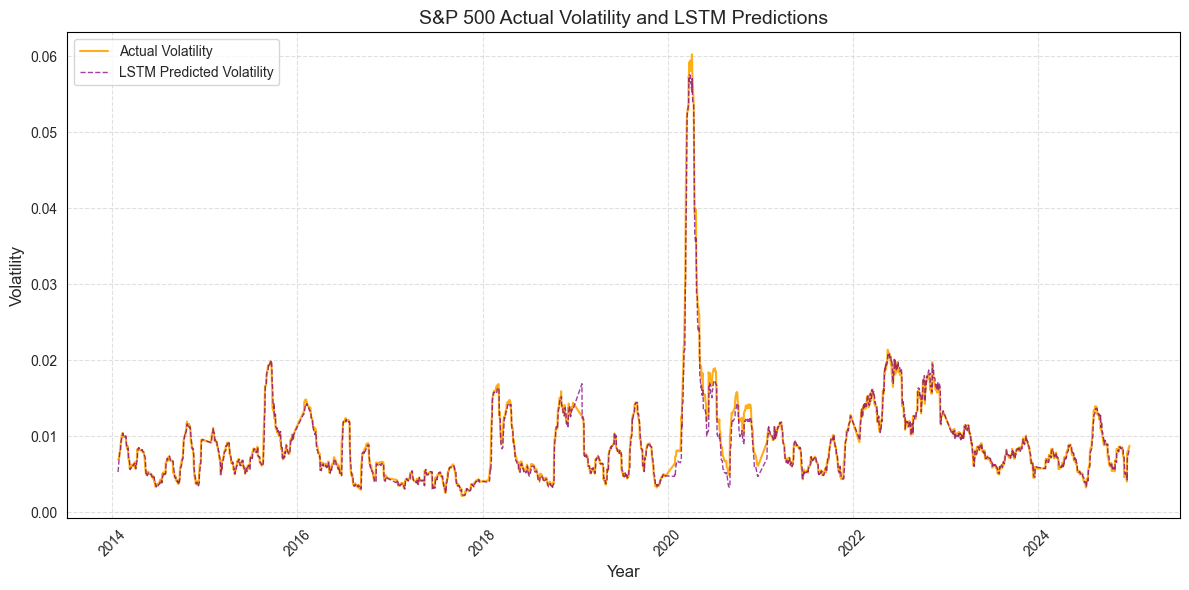
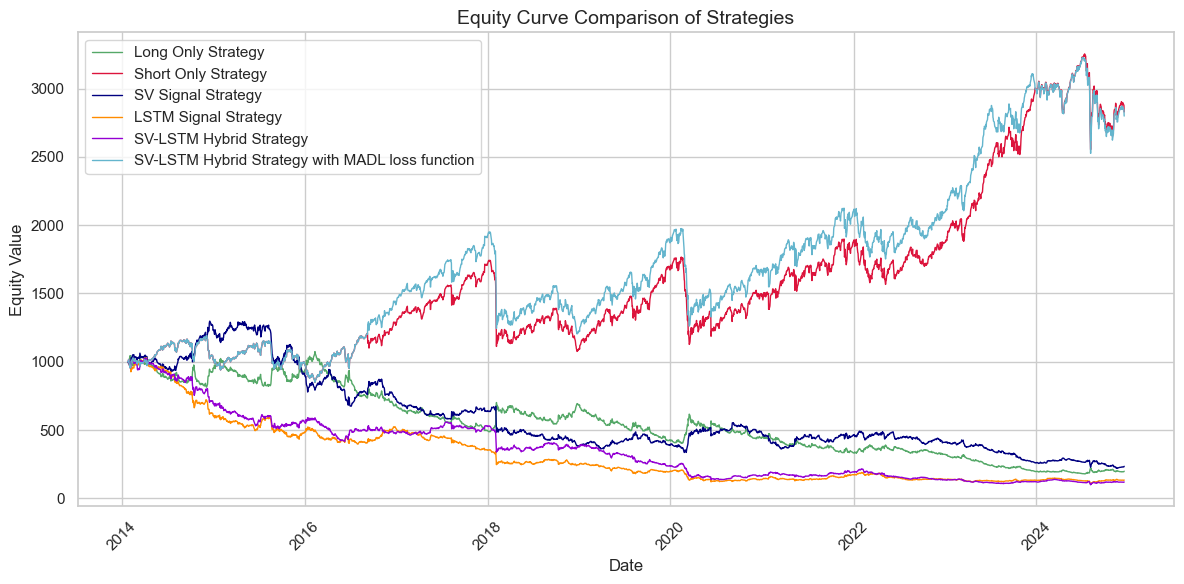
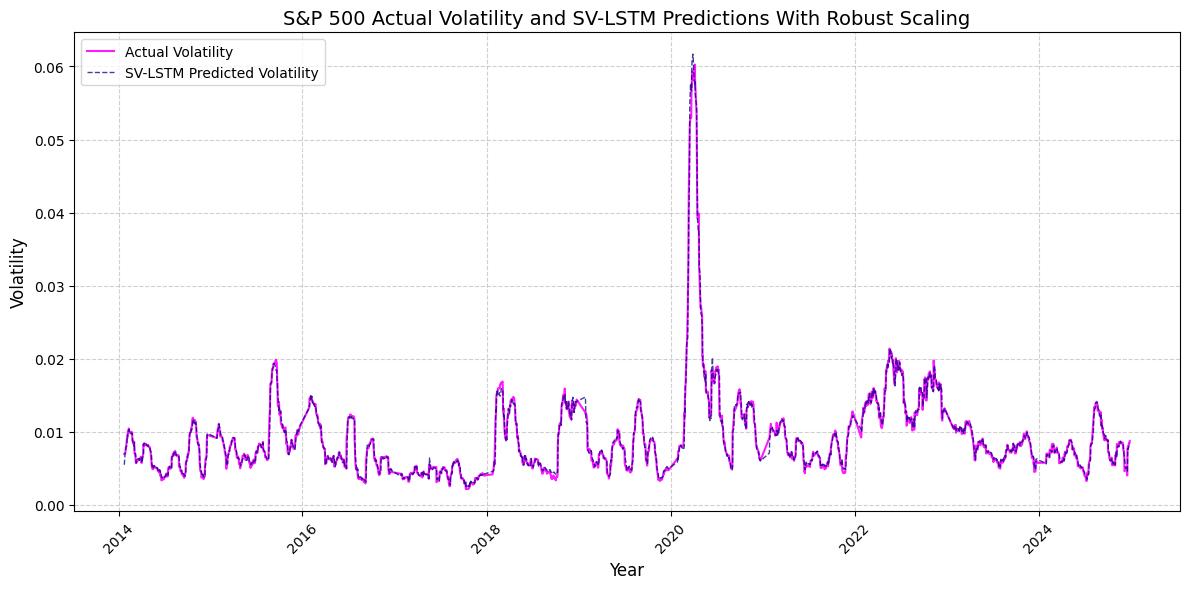
Accurate volatility forecasting is essential in banking, investment, and risk management, because expectations about future market movements directly influence current decisions. This study proposes a hybrid modelling framework that integrates a Stochastic Volatility model with a Long Short Term Memory neural network. The SV model improves statistical precision and captures latent volatility dynamics, especially in response to unforeseen events, while the LSTM network enhances the model's ability to detect complex nonlinear patterns in financial time series. The forecasting is conducted using daily data from the S and P 500 index, covering the period from January 1 1998 to December 31 2024. A rolling window approach is employed to train the model and generate one step ahead volatility forecasts. The performance of the hybrid SV-LSTM model is evaluated through both statistical testing and investment simulations. The results show that the hybrid approach outperforms both the standalone SV and LSTM models and contributes to the development of volatility modelling techniques, providing a foundation for improving risk assessment and strategic investment planning in the context of the S and P 500.
The demand for accurate volatility forecasts reflects their central role in risk management, asset pricing, and portfolio optimization. Financial market participants rely on these forecasts to guide investment strategies and assess risk exposure. While models such as GARCH and SV capture the stochastic nature of volatility, incorporating LSTM networks can enhance predictions by identifying non-linear patterns. This study addresses a gap in financial forecasting research by proposing a hybrid SV-LSTM model that leverages both the statistical strengths of SV and the pattern-recognition capacity of LSTM.
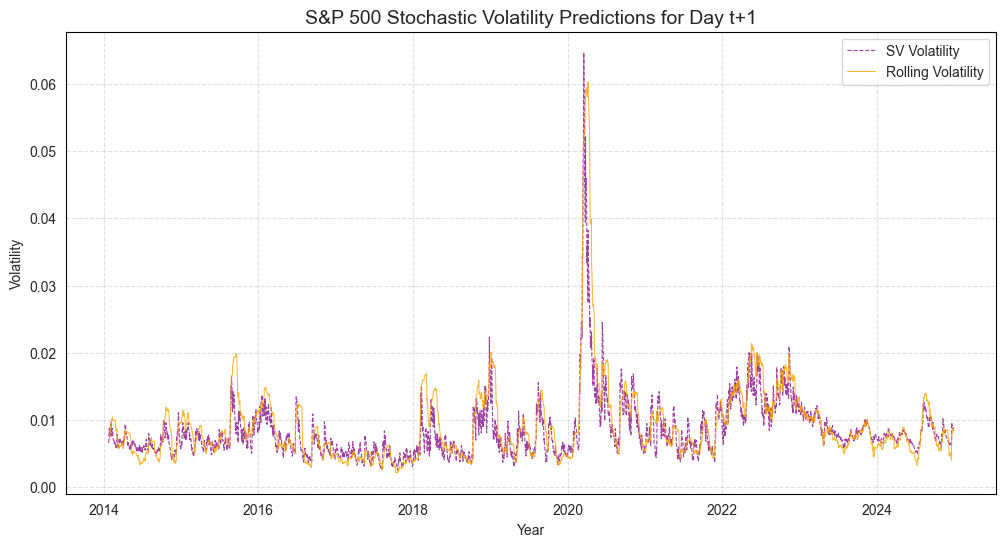
The objective is to assess whether incorporating latent volatility estimates from an SV model as an additional input enhances the predictive performance of the LSTM model compared to their standalone applications.
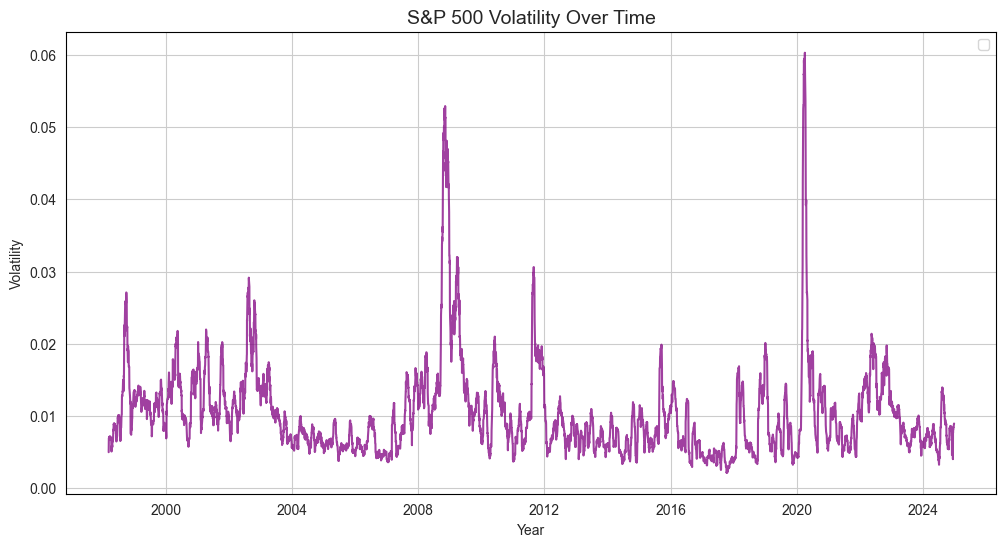
The main focus of the forecast was chosen to be the volatility of the S&P 500 index, a well-established measure of market fluctuations.
The research conducted in this paper is guided by the following central hypotheses:
• H1: The inclusion of stochastic volatility forecasts for day t+1 enhances the predictive accuracy of the LSTM model.
• H2: Augmenting the input data of the LSTM model with external information beyond historical returns improves its forecasting performance.
• H3: The hybrid SV-LSTM model delivers enhanced volatility forecasts compared to the standalone SV model.
In addition to the main hypotheses, the following secondary research questions are investigated:
• RQ1: Increasing the dimensionality of inputs from the SV model further improves the predictive performance of the hybrid model.
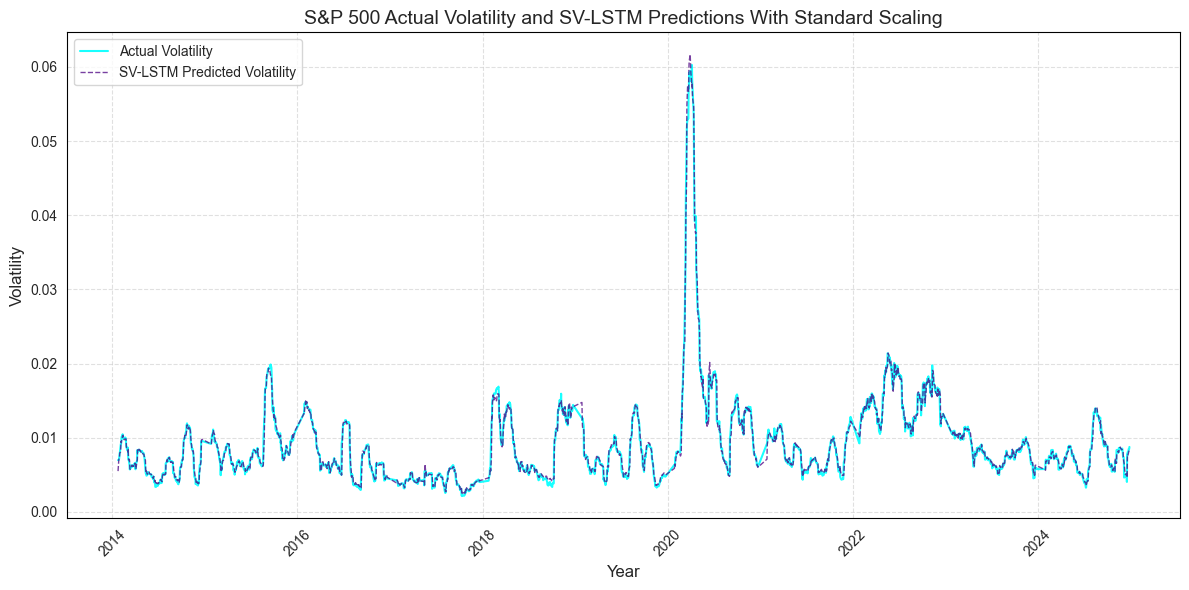
• RQ2: The preprocessing and transformation of input data have a significant effect on the performance of the SV-LSTM model.
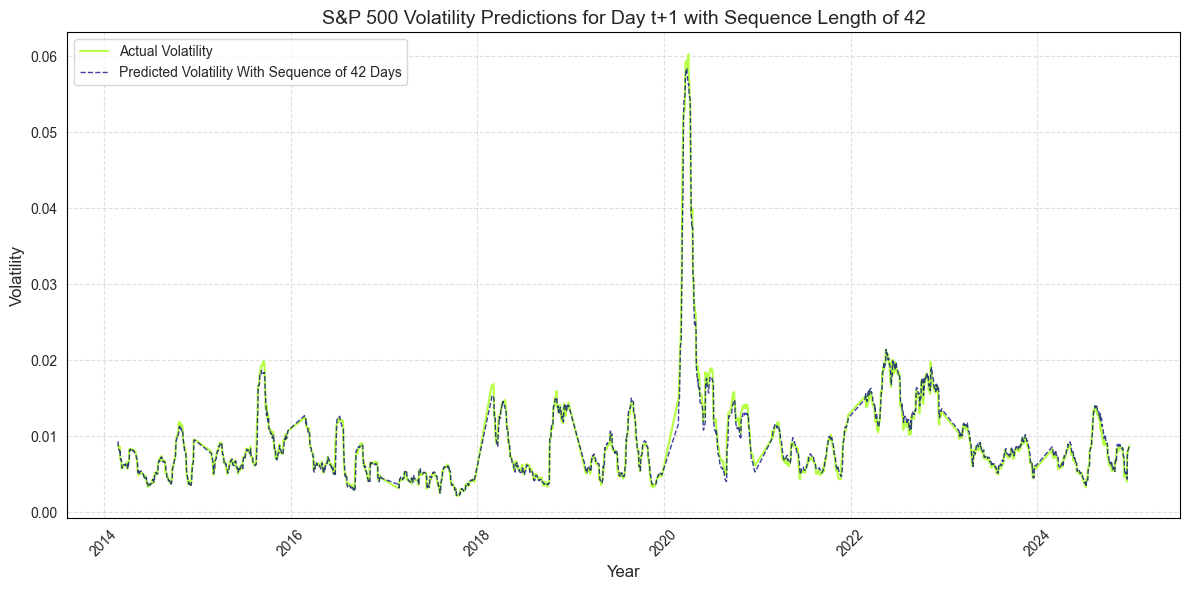
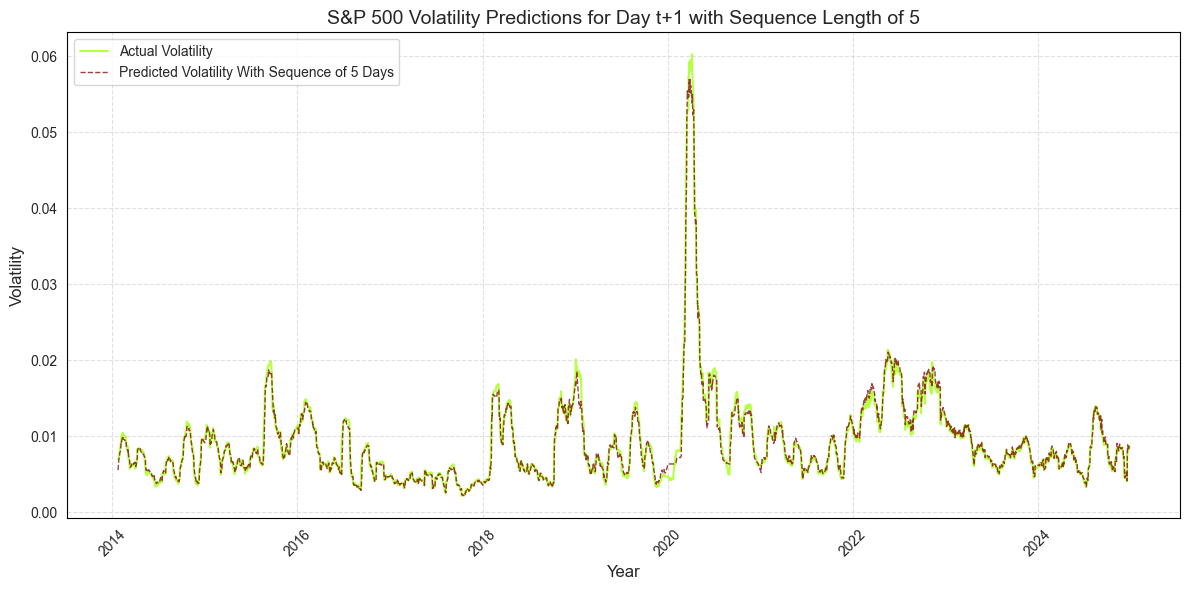
• RQ3: The decreased sequence of the input data into the LSTM model improves the SV-LSTM prediction accuracy.
The data used is daily close price for the S&P 500 index, covering the period from January 1, 1998, to December 31, 2024, obtained from the YahooFinance.
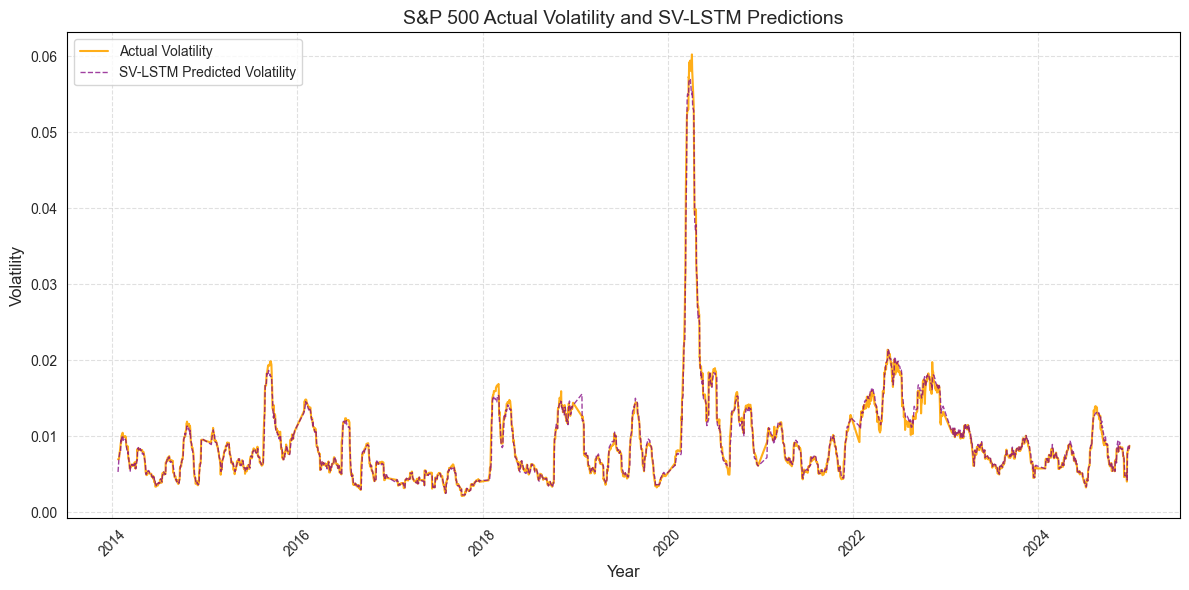
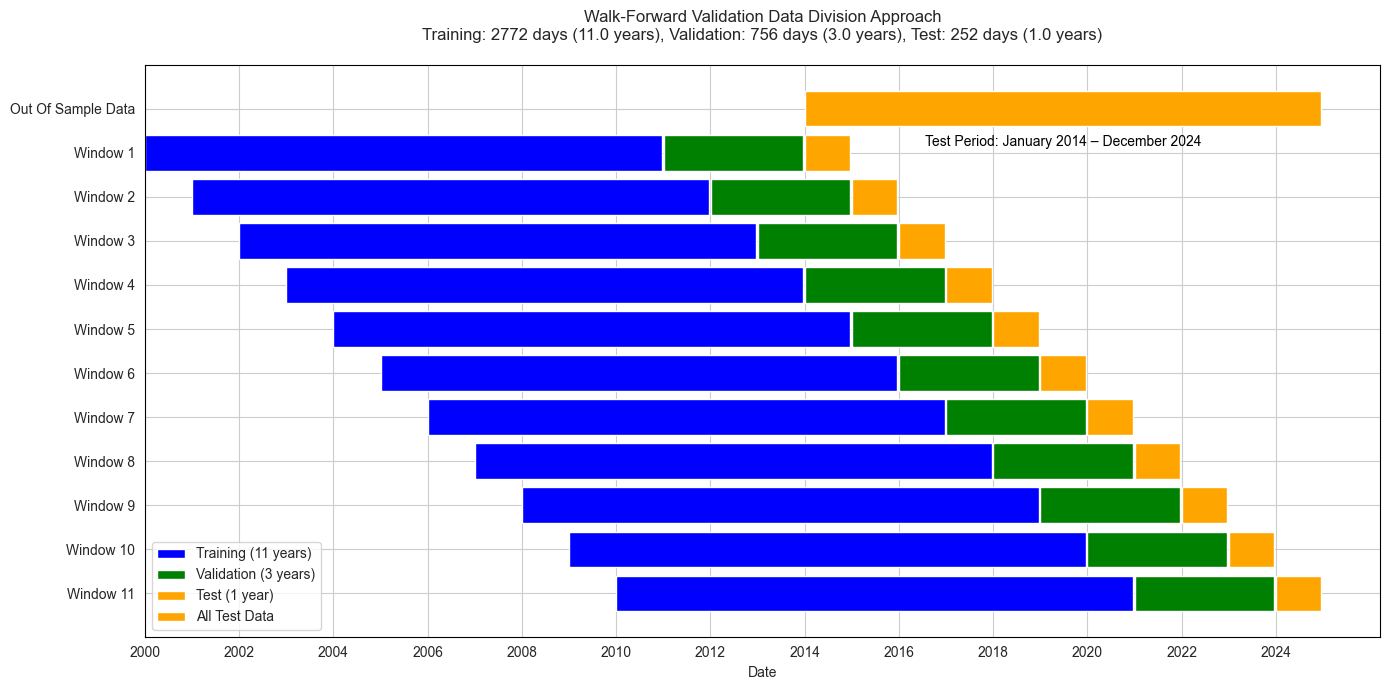
The methodology employed in this thesis involves a combination of stochastic volatility modeling, LSTM networks and statistical testing. The SV model is used to generate volatility forecasts, which are then incorporated as inputs to the LSTM model. Additionally, benchmarks, including standalone LSTM and SV models, are introduced to compare the performance of the hybrid SV-LSTM model. The Wilcoxon Signed-Rank and Diebold-Mariano Tests are used to statistically evaluate the significance of the differences in predictive performance between the models.
This study contributes to financial modeling by examining the combination of a statistical SV model as input to a machine learning LSTM model. It is the first to investigate the impact of incorporating SV predictions of latent volatility into the LSTM architecture. This hybrid approach captures both latent stochastic processes and nonlinear dependencies in financial time series, improving the model’s ability to reflect unpredictable market dynamics. The step-by-step framework, supported by sensitivity analysis and statistical testing, bridges the gap between deep learning techniques and traditional econometric approaches. Practically, the study demonstrates relevance through a simulated investment strategy, highlighting potential improvements in portfolio risk management, dynamic asset allocation, and algorithmic trading, and offering tools for more adaptive and resilient investment strategies in volatile markets.
The structure of the thesis is as follows:
The second chapter provides a review of literature on both classical volatility models and hybrid financial forecasting. The third chapter presents the dataset used, preprocessing techniques and error metrics. The fourth chapter outlines the methodology for three models involved in the model development: SV model, LSTM and hybrid SV-LSTM. The fifth chapter compares the models’ performance using statistical tests, while the sixth chapter explores the robustness of the results through sensitivity analysis. Finally, the seventh chapter summarizes the key findings, discusses their implications, and reflects on the achievement of the research objectives.
The early development of financial econometric models was founded on the assumption of constant volatility, which was most notably formalized in the seminal work of Black and Scholes (1973). Their option pricing model introduced a cornerstone framework that assumed volatility to be constant over time, providing analytical tractability and laying the foundation for modern financial derivatives pricing. However, when confronted with empirical evidence from financial markets and clustering behavior, this simplifying assumption soon revealed substantial limitation.
The assumption of constant volatility was first formally challenged by Engle (1982), who introduced the Autoregressive Conditional Heteroskedasticity (ARCH) model. This framework allowed volatility to evolv
This content is AI-processed based on open access ArXiv data.