Attribution methods are among the most prevalent techniques in Explainable Artificial Intelligence (XAI) and are usually evaluated and compared using Fidelity metrics, with Insertion and Deletion being the most popular. These metrics rely on a baseline function to alter the pixels of the input image that the attribution map deems most important. In this work, we highlight a critical problem with these metrics: the choice of a given baseline will inevitably favour certain attribution methods over others. More concerningly, even a simple linear model with commonly used baselines contradicts itself by designating different optimal methods. A question then arises: which baseline should we use? We propose to study this problem through two desirable properties of a baseline: (i) that it removes information and (ii) that it does not produce overly out-of-distribution (OOD) images. We first show that none of the tested baselines satisfy both criteria, and there appears to be a trade-off among current baselines: either they remove information or they produce a sequence of OOD images. Finally, we introduce a novel baseline by leveraging recent work in feature visualisation to artificially produce a model-dependent baseline that removes information without being overly OOD, thus improving on the trade-off when compared to other existing baselines. Our code is available at https://github.com/deel-ai-papers/Back-to-the-Baseline
Recent advances in the field of Machine Learning have led to models capable of solving increasingly complex tasks, albeit at the expense of opacity in the strategies they implement [16,37,39,44]. Out of this need, a new field was created -eXplainable Artificial Intelligence (XAI) -, and within, plenty of different approaches to understanding these so-called "black-boxes" cropped up [11,40,27,22,18,50,10]. One of the most notable is attribution methods [70,71,56,49], which attempt to explain the model's predictions by finding the pixels or area deemed most important in an image for a given prediction.
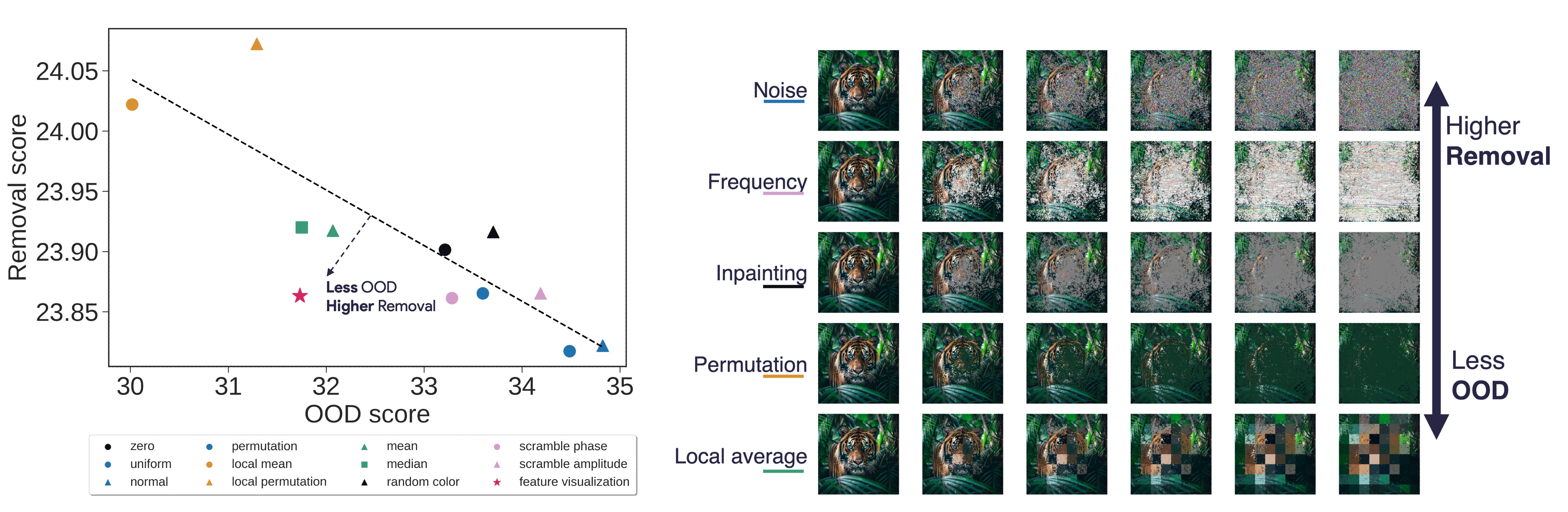
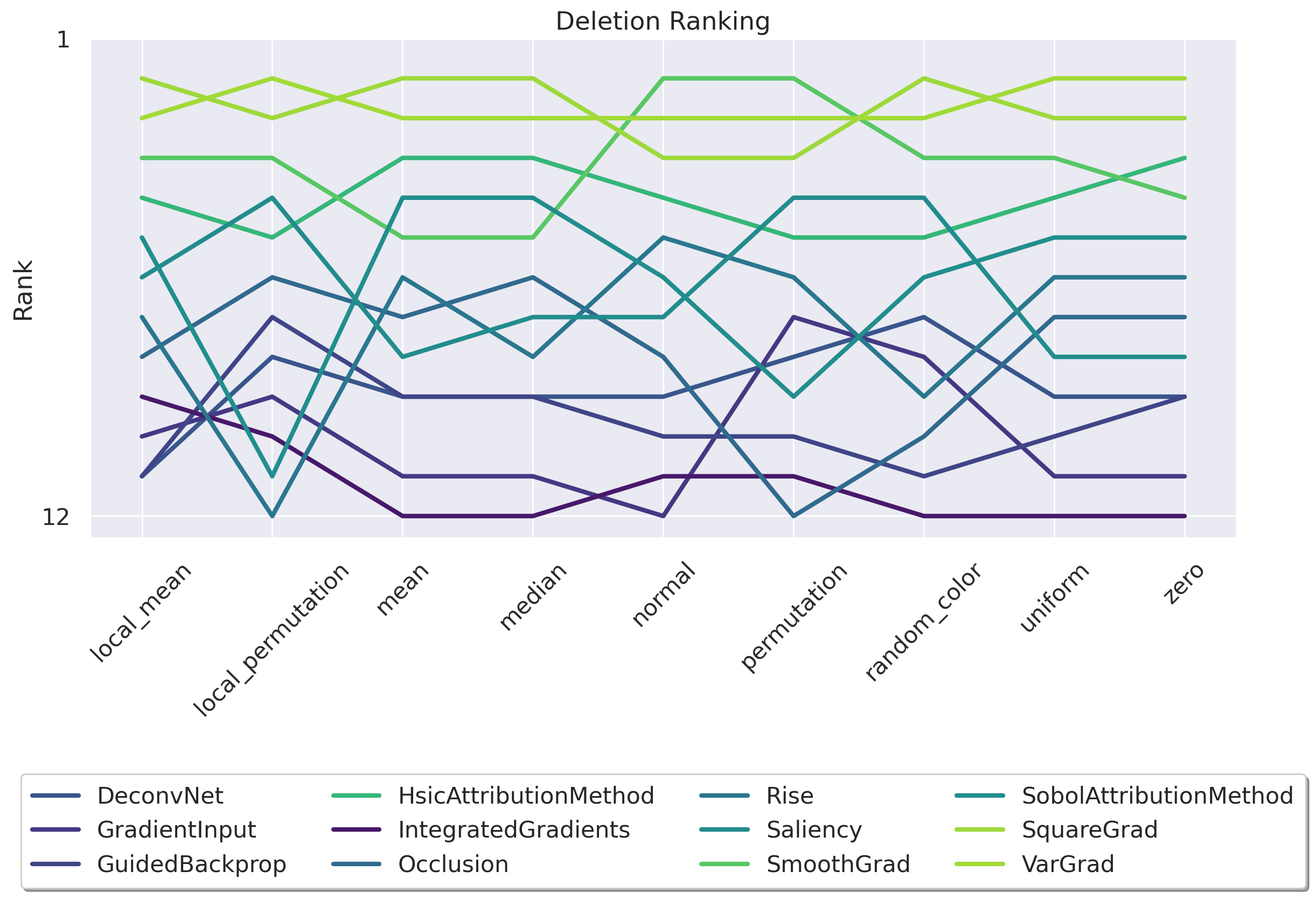
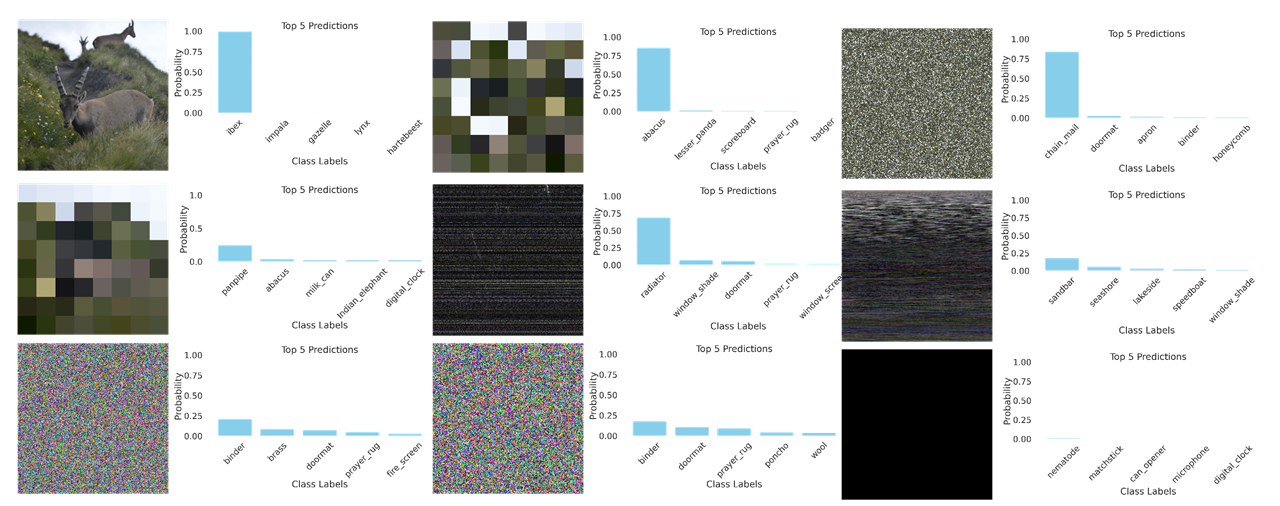
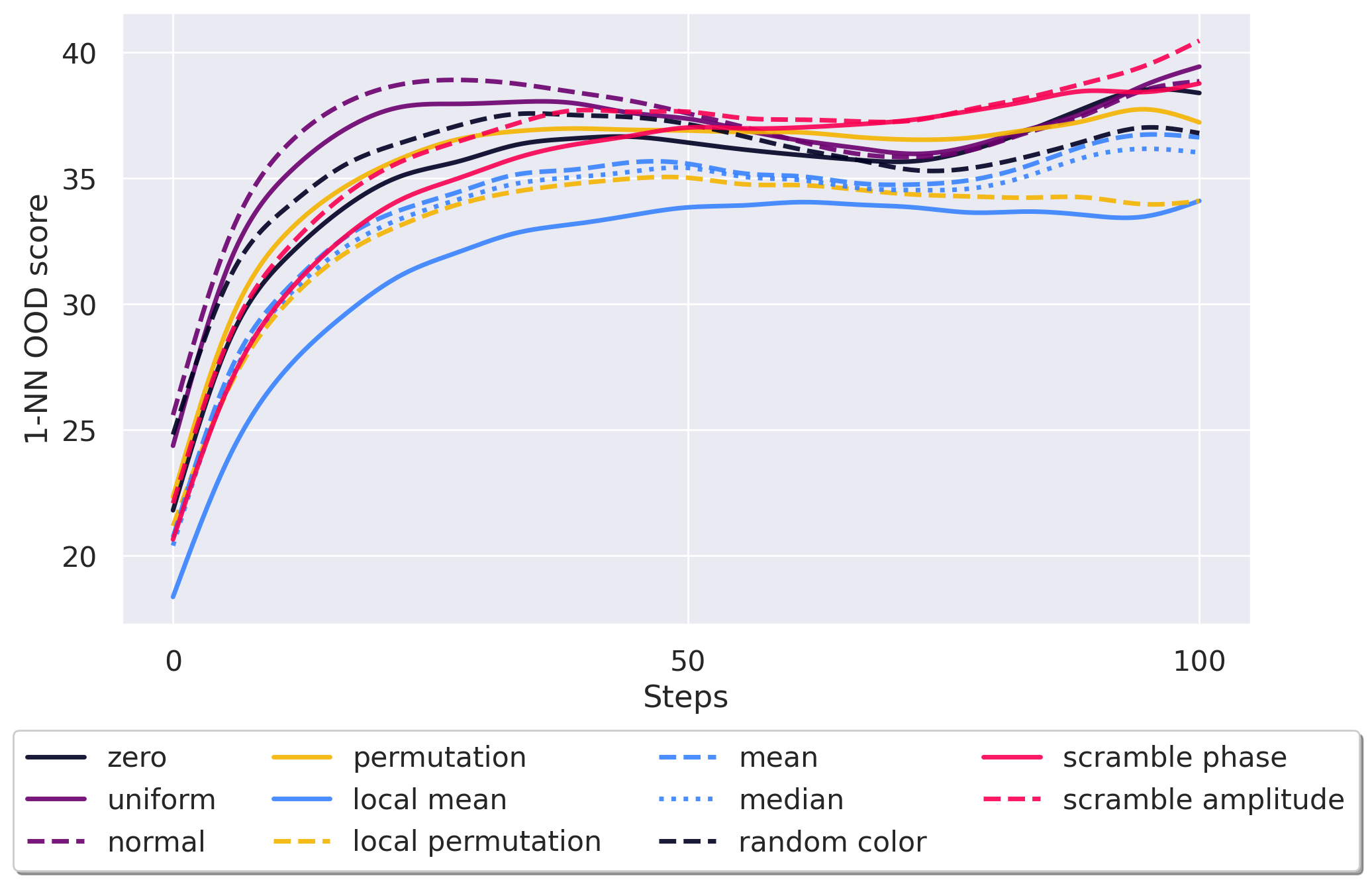
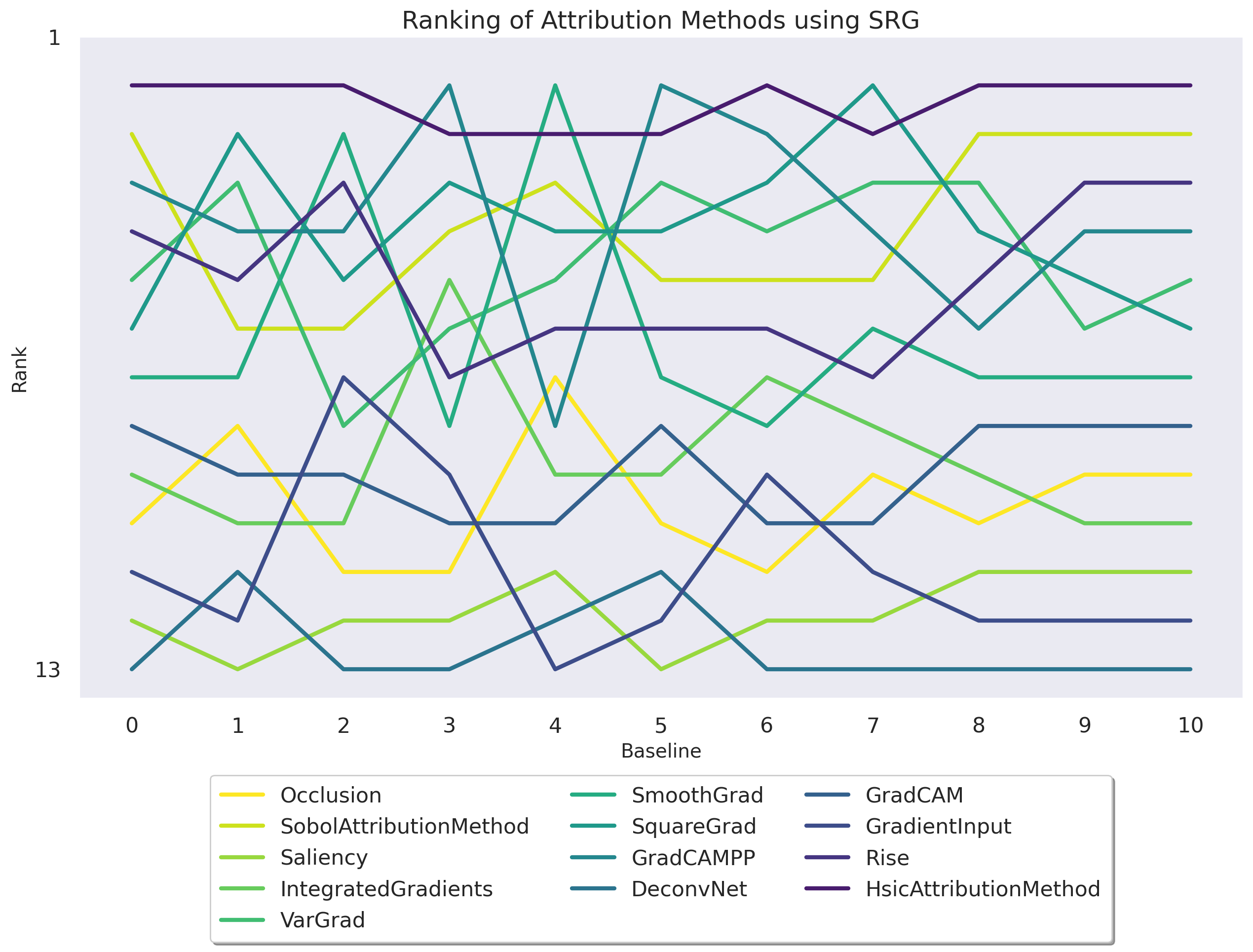
Figure 1: A) Deletion ranking is highly sensitive to the baseline. We study the impact of the choice of the baseline on measuring the faithfulness of attribution methods for the same ResNet50 [29] trained on ImageNet1k [45](See Appendix D for results on a ViT [17]). Our analysis reveals that the performance of attribution methods under the Deletion metric [51] is highly dependent on the chosen baseline, suggesting that the selection of a baseline can be manipulated to favor particular methods. B) Example of how the baseline modifies an input image. Given an input-explanation pair (x, γ), we replace the most important pixels of x given by γ with a series of different baselines.
The applications of these techniques are diverse -from aiding in refining or troubleshooting model decisions to fostering confidence in their reliability [16]. However, a significant drawback of these methods is their susceptibility to confirmation bias: although they seem to provide meaningful explanations to human researchers, they might generate incorrect interpretations [1,26,59]. In other words, the fact that the explanations are understandable to humans does not guarantee they accurately represent the model’s internal processes. Consequently, the field is actively pursuing improved benchmarks by introducing Fidelity (or Faithfulness) metrics [55,51,6,36,31,21,43,30].
These so-called Fidelity metrics measure how closely the explanation reflects the model’s local behaviour. This is typically done by using the explanations to carefully pick parts of the input, replacing them with an arbitrary baseline, and then measuring the impact on the model’s output. Hence, the outcome of this procedure heavily depends on how the impact on the model is measured precisely, as well as on the choice of the baseline and its interaction with the model and the specificities of the attribution method. We will show later that certain baselines will inherently favour certain types of attribution methods.
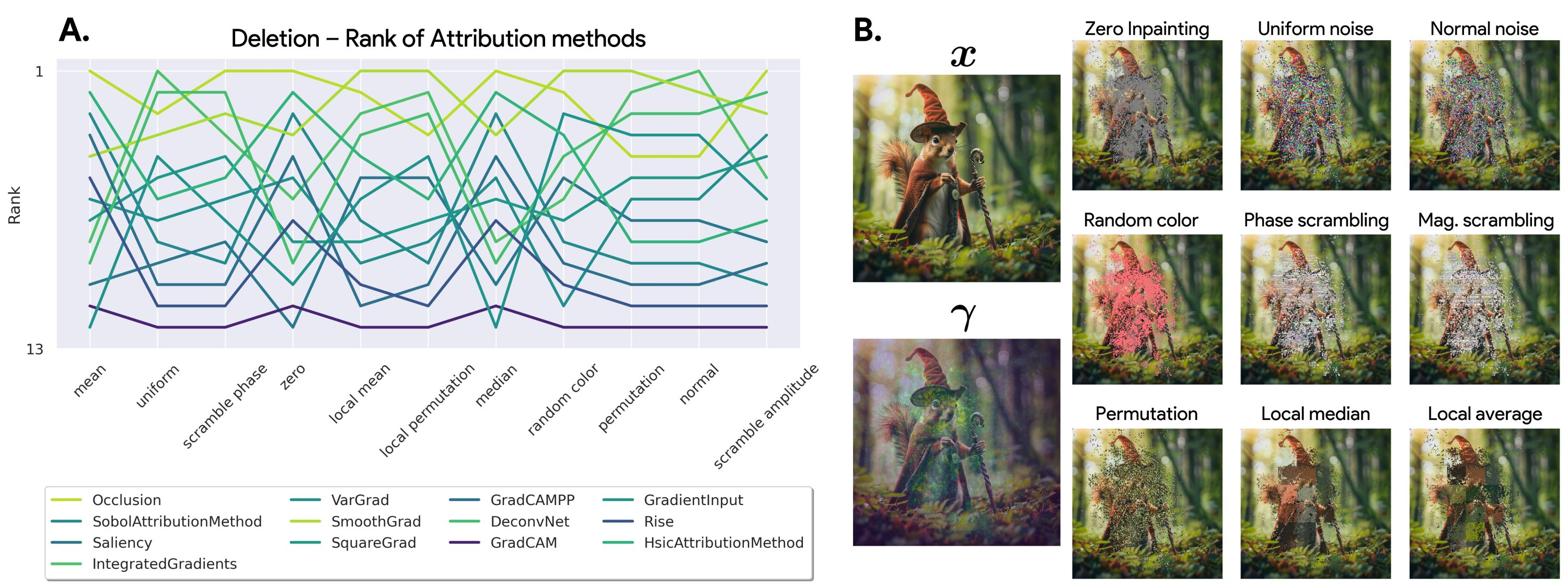
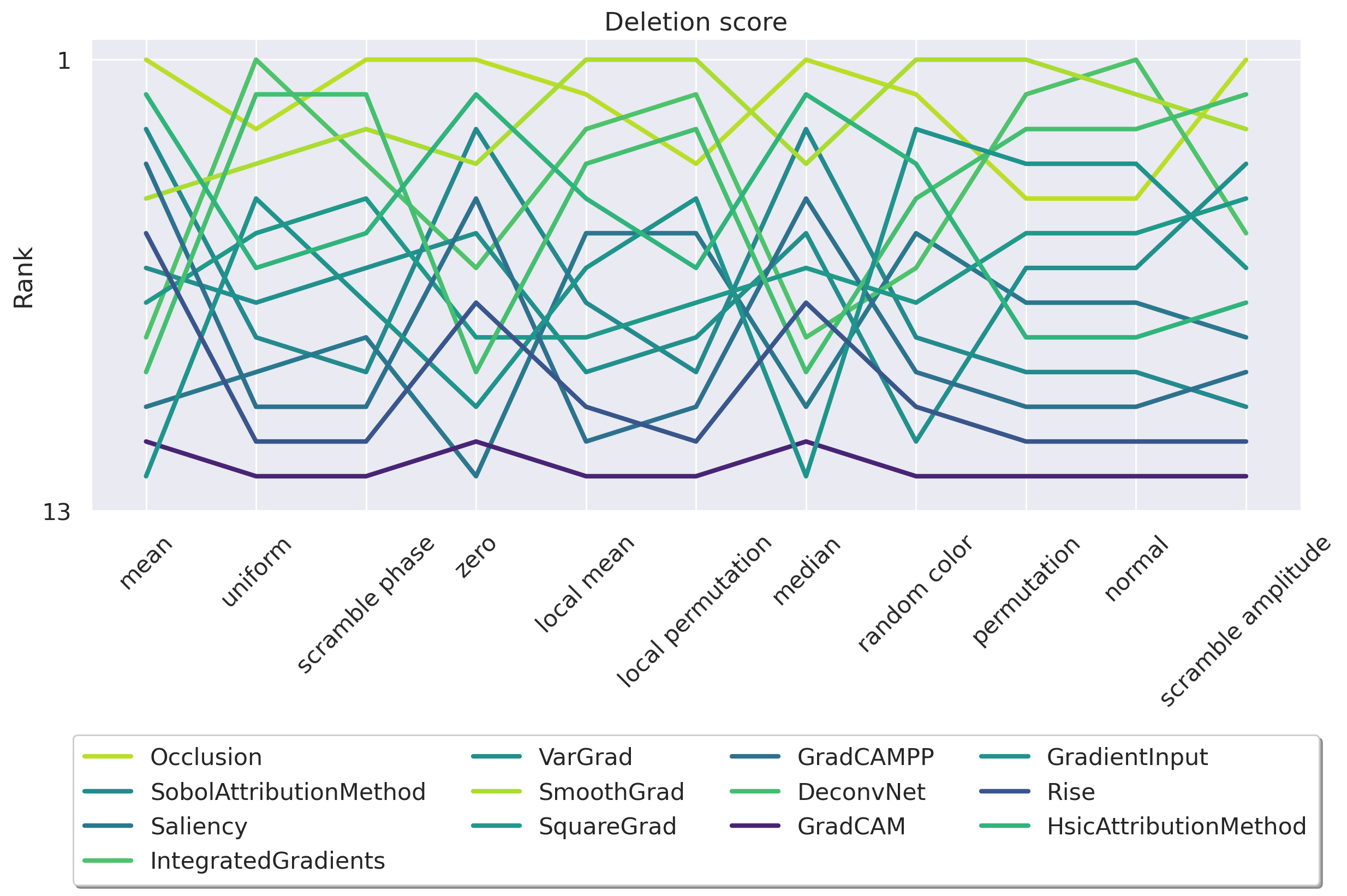
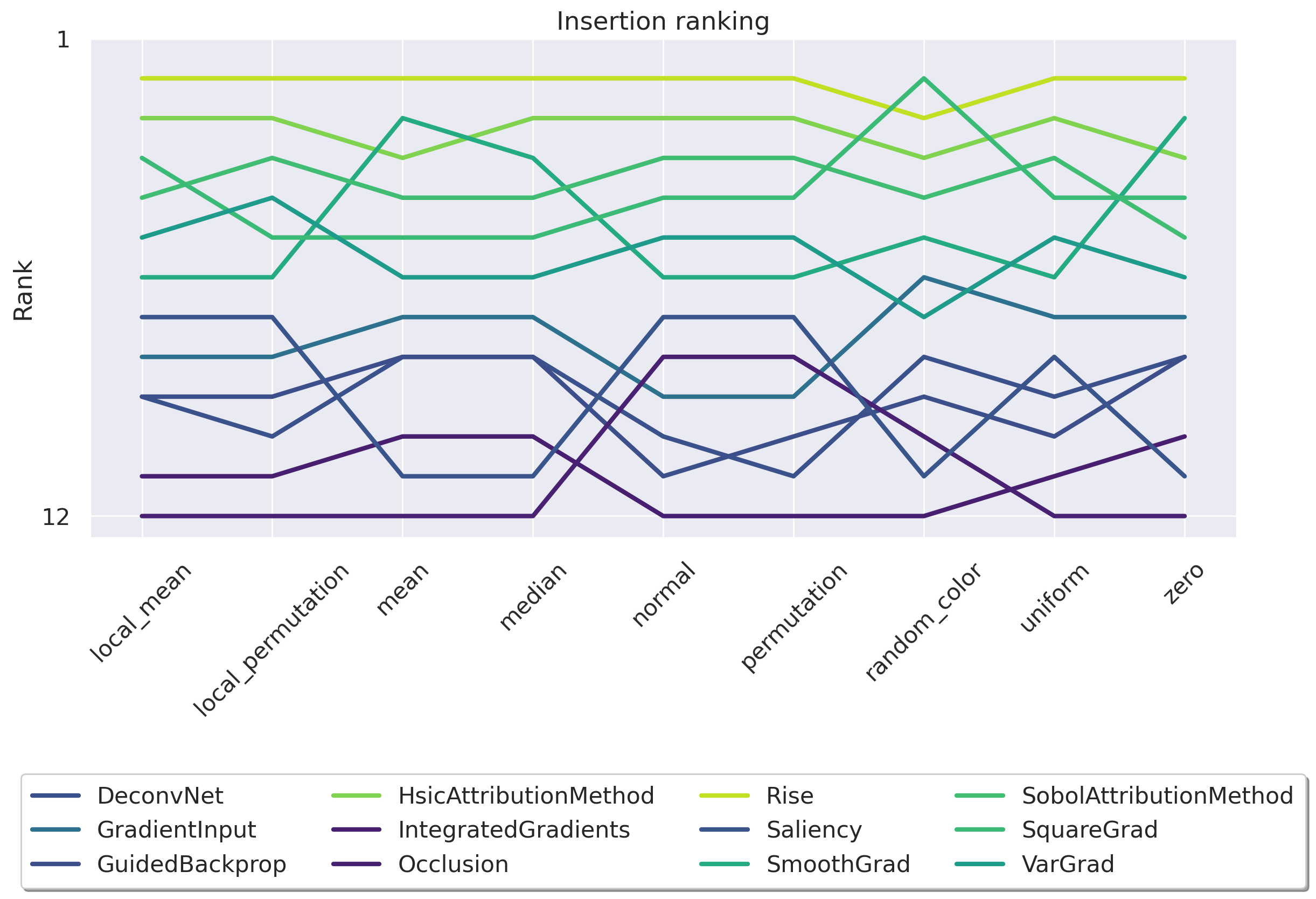
While these metrics mark significant progress for the field, one crucial question remains unanswered: each faithfulness metric relies on substituting parts of the input with a baseline function. As shown in Figure 1, the choice of this baseline significantly affects the ranking of different attribution methods. This leads to two key questions we aim to address in this work: (i) Can we find the origin of this instability to explain why the ranking using Deletion is unstable while the ranking using Insertion appears stable (see Figure 2)? (ii) What baseline should we choose?
This paper explores these questions and presents the following findings:
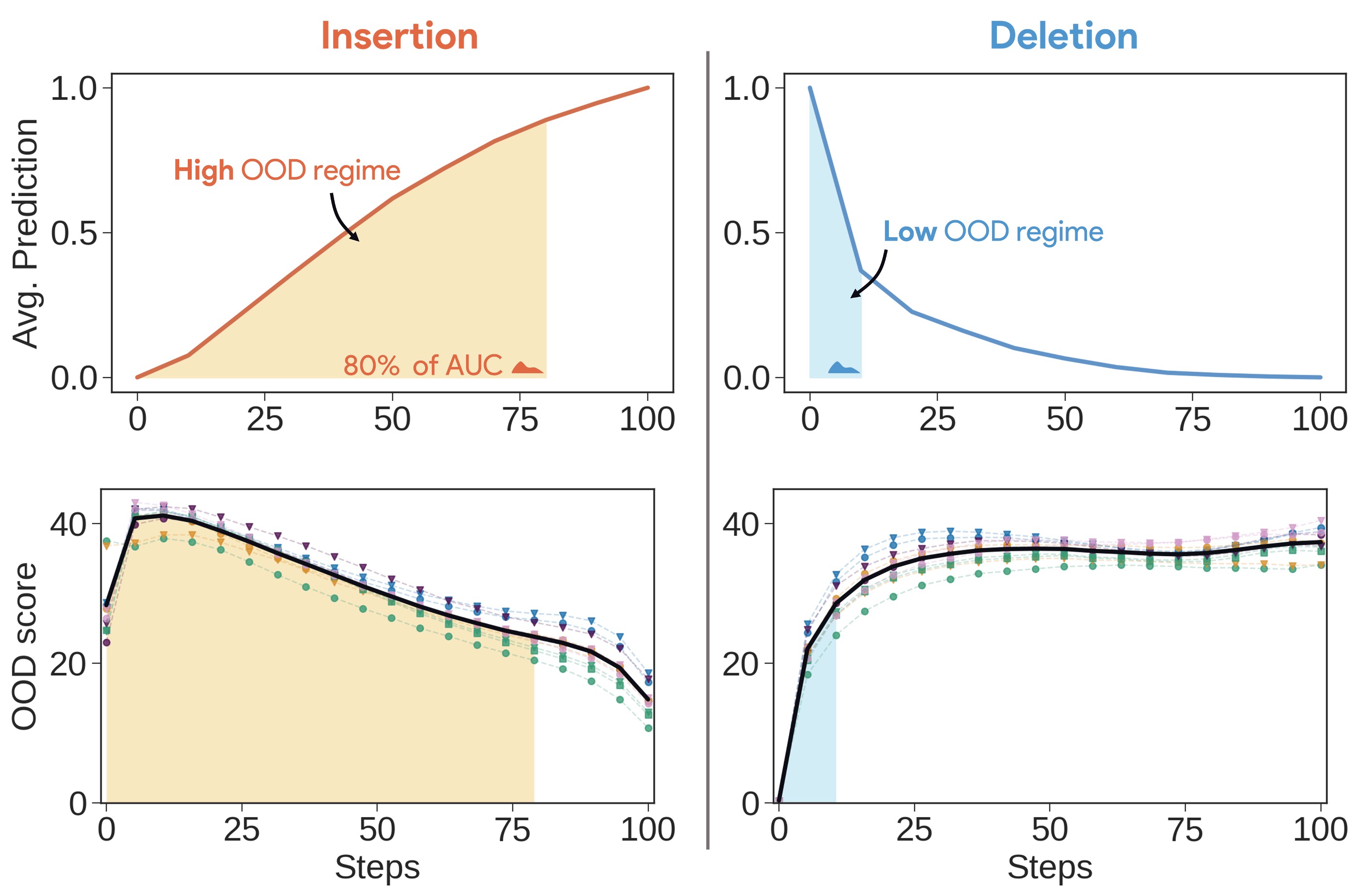
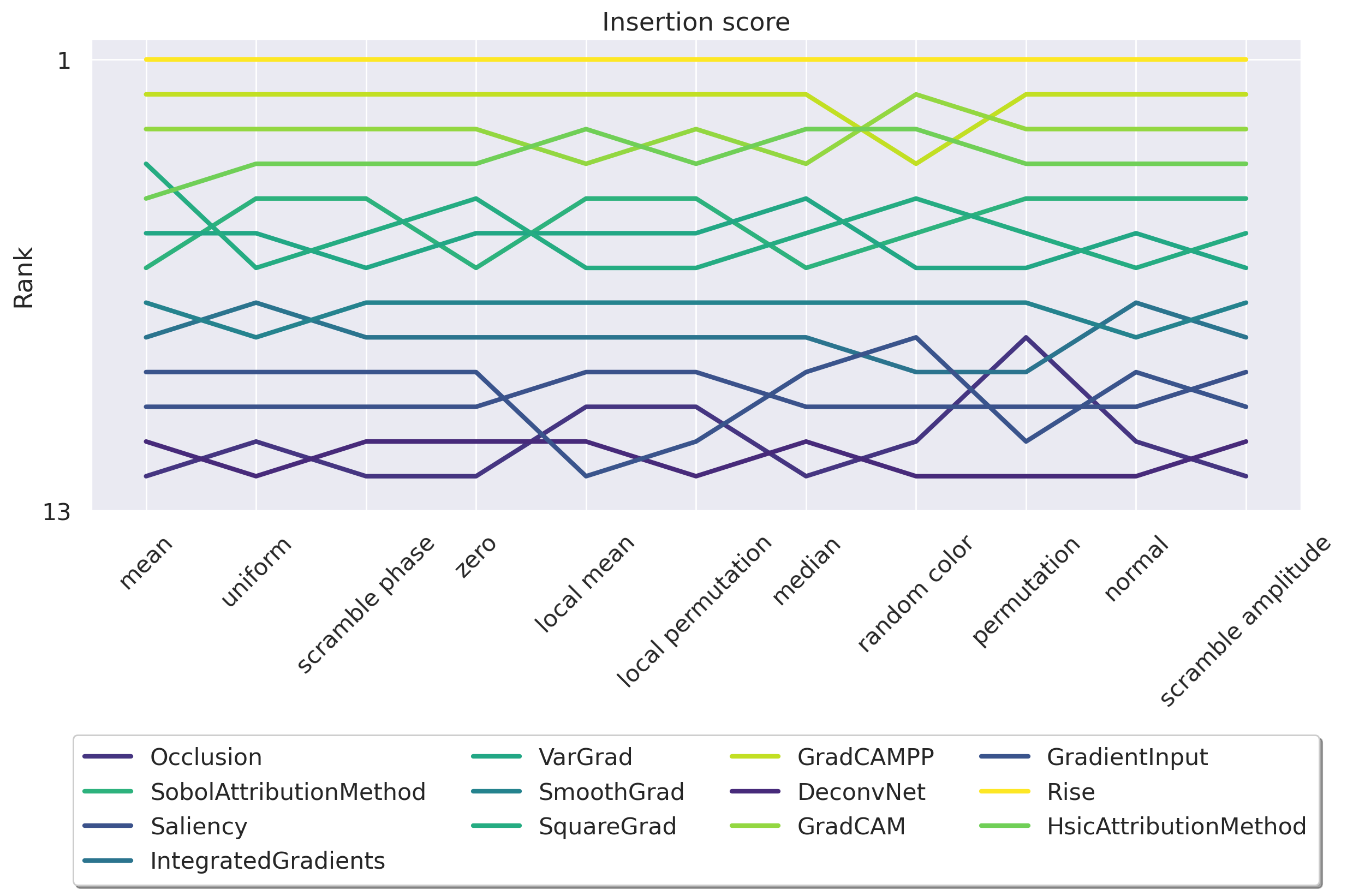
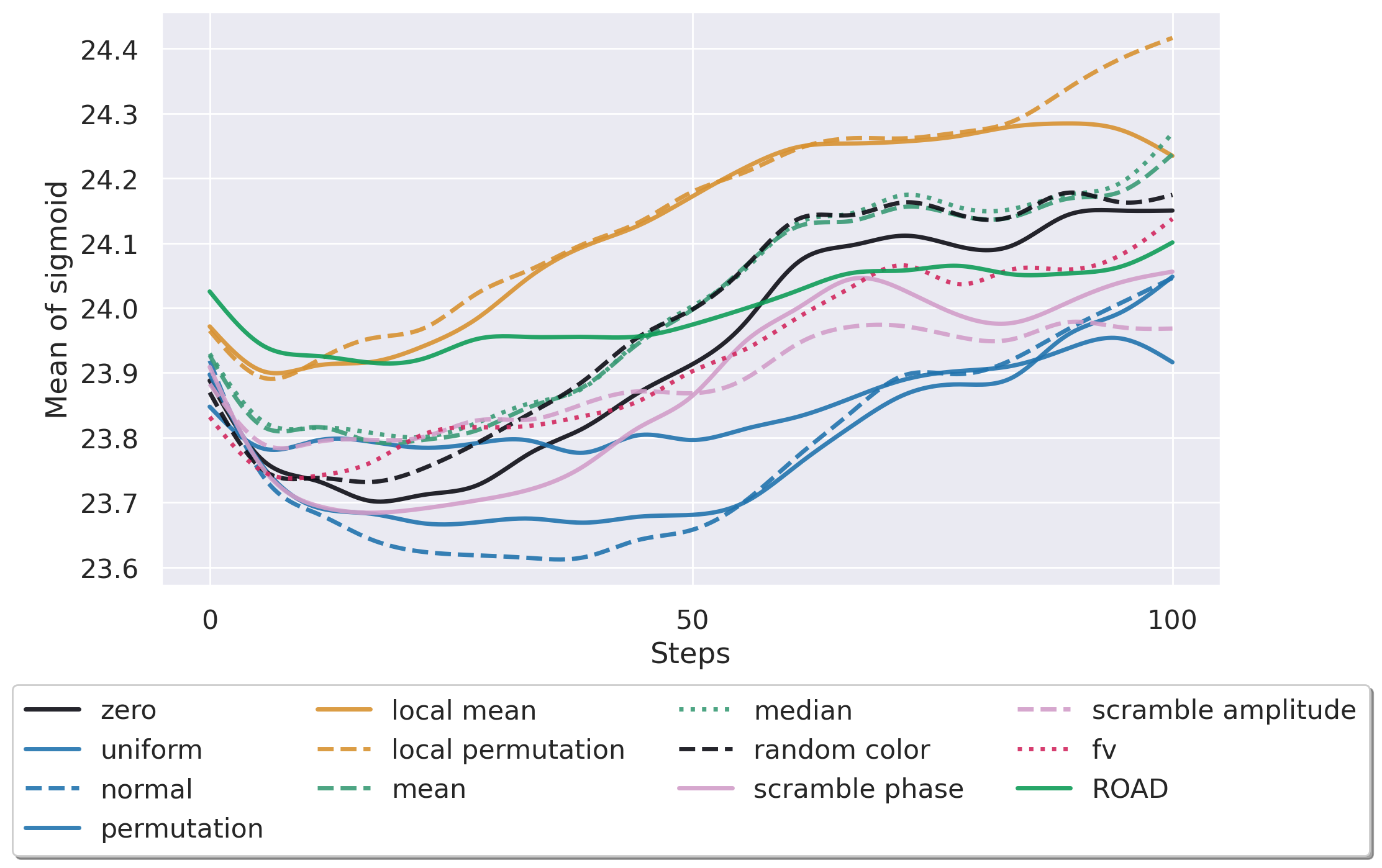
• We begin by demonstrating that the Deletion metric is highly dependent on the baseline choice, rendering it unreliable for comparing attribution methods. In contrast, the Insertion metric appears stable, but it hides a critical flaw: 80% of its score is achieved in the high Figure 2: Insertion ranking of attribution methods is more stable than Deletion. We investigate how different baseline choices affect the assessment of attribution method faithfulness for a ResNet50 [29] model trained on ImageNet1k [45] (See Appendix D for ViT results). We evaluate Insertion across a series of attribution methods from the literature using 11 different baselines (see Appendix E for more details) on a total of 14,000 explanations. Although much more stable than Deletion, the OOD-ness of the different baselines makes this metric unreliable.
out-of-distribution (OOD) regime. Conversely, 80% of Deletion’s score occurs in a non-OOD regime, raising concerns about the reliability of Insertion.
• We confirm this instability theoretically: even with a simple theoretical example, we demonstrate that for a linear class of models, the optimal attribution for Deletion and Insertion can vary significantly. Depending on the chosen baseline, the optimal attribution could be Saliency [58], Occlusion [71], RISE [51], Gradient-Input [57], or Integrated Gradients [65].
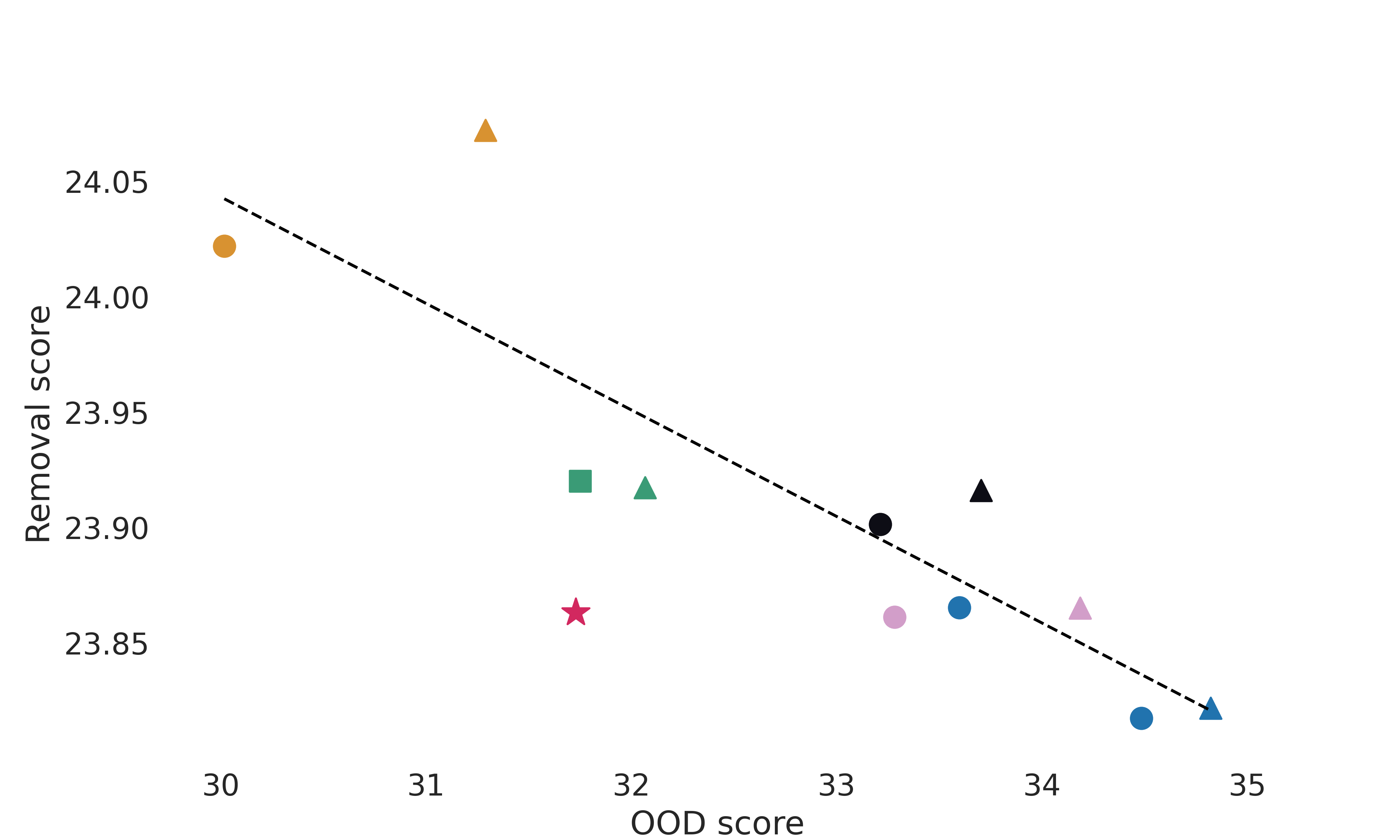
• After investigating the impact and the source of instability, we propose to evaluate the various baselines through two desiderata identified earlier: the out-of-distribution (OOD) score of a baseline and its information removal score. Essentially, the ability to remove information without causing a significant distributional shift. By leveraging quantitative measures, we ob
This content is AI-processed based on open access ArXiv data.