Monte Carlo Tree Search is a cornerstone algorithm for online planning, and its root-parallel variant is widely used when wall clock time is limited but best performance is desired. In environments with continuous action spaces, how to best aggregate statistics from different threads is an important yet underexplored question. In this work, we introduce a method that uses Gaussian Process Regression to obtain value estimates for promising actions that were not trialed in the environment. We perform a systematic evaluation across 6 different domains, demonstrating that our approach outperforms existing aggregation strategies while requiring a modest increase in inference time.
Monte Carlo Tree Search (MCTS) is a widely used online planning algorithm. Its anytime nature, ability to plan from the present state, and requirement for only sample-based access to the transition and reward functions have lead to successful applications in practical domains with large state and action spaces (Silver and Veness 2010;Silver et al. 2016). MCTS relies on the quality of simulation returns, which poses challenges for identifying strong actions when only limited time or simulation budgets are available. Rootparallel MCTS (Cazenave and Jouandeau 2007), which performs independent MCTS runs with different random initializations and aggregates results to yield the final action, improves performance over single thread MCTS especially in low time or computation budgets.
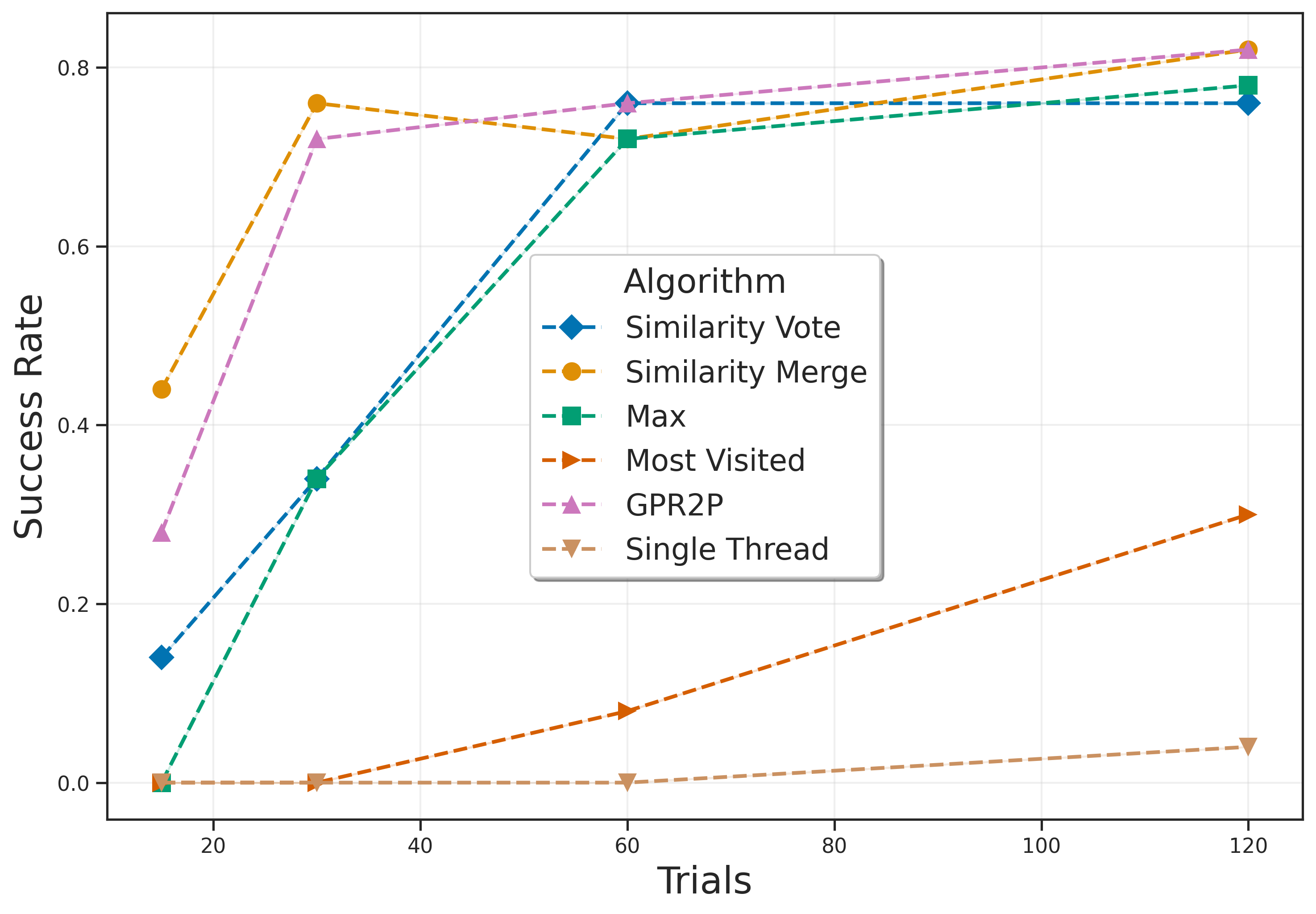
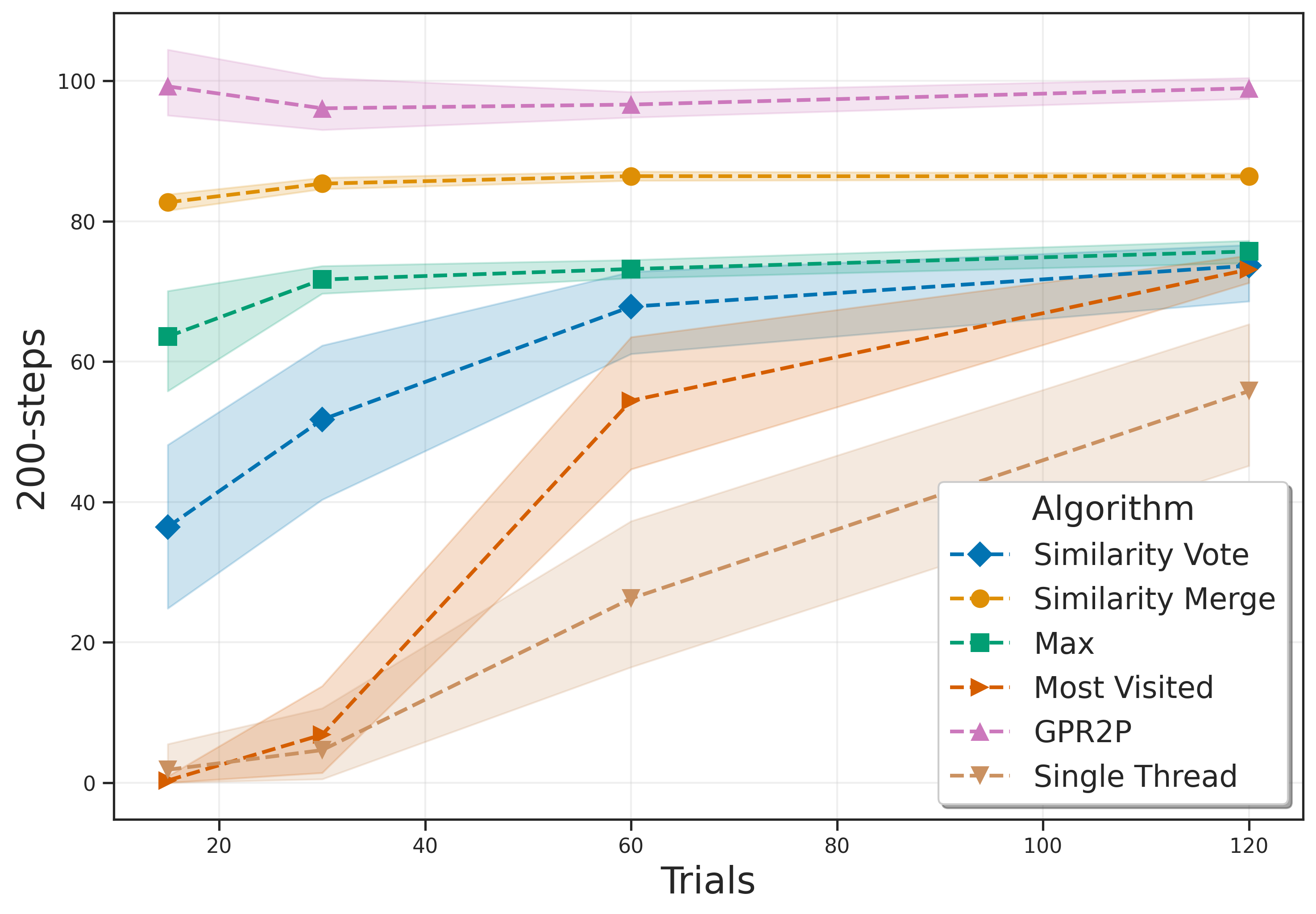
Determining the best way to aggregate results in rootparallel MCTS remains an important challenge, particularly in continuous actions domains. Unlike in domains with discrete actions, each sampled action is unique, rendering the typical Majority Voting (Soejima, Kishimoto, and Watanabe 2010) approach inapplicable. Adopting the action with highest return (Max) and visit count (Most Visited) across the threads are sensible baseline strategies. State-of-the-art methods aim to exploit the relationships among the returns of individual actions (Kurzer, Hörtnagl, and Zöllner 2020). Intuitively, when starting from the same state, similar actions (e.g., as quantified by a distance metric) will drive the agent towards similar subsequent states, which in turn increases the likelihood of obtaining similar simulation returns compared to completely different actions.
However, important limitations remain. Firstly, such methods lack a mechanism for interpolating between sampled actions. While the returns of actions will influence those of nearby ones as quantified by the distance metric, the methods cannot output actions that were not trialed in the tree, a significant downside in action spaces with meaningful structure. Secondly, the benefit of such approaches relative to single thread MCTS and simple baselines remains unclear. Currently, a thorough evaluation of aggregation strategies for root-parallel MCTS is lacking in the literature.
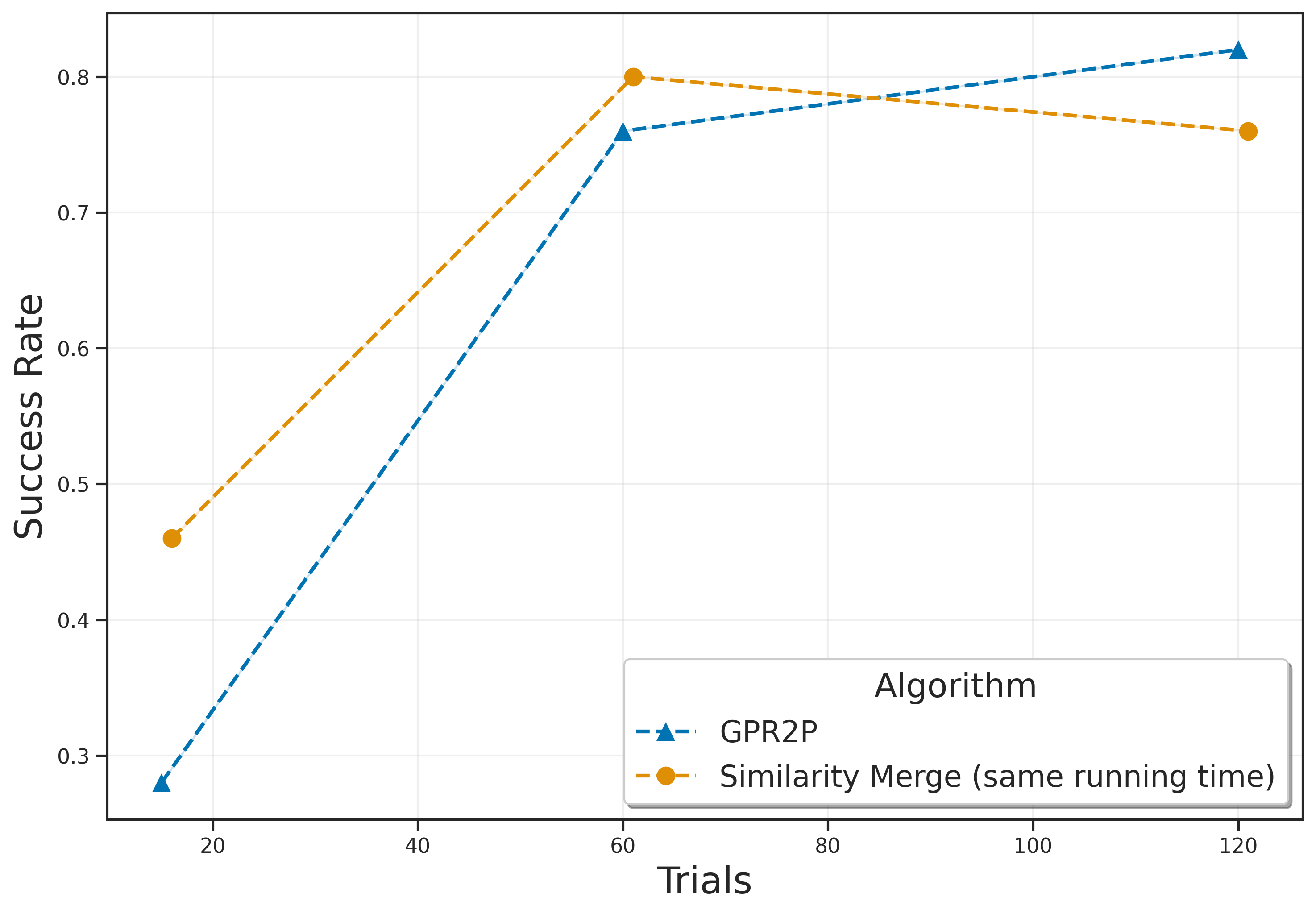
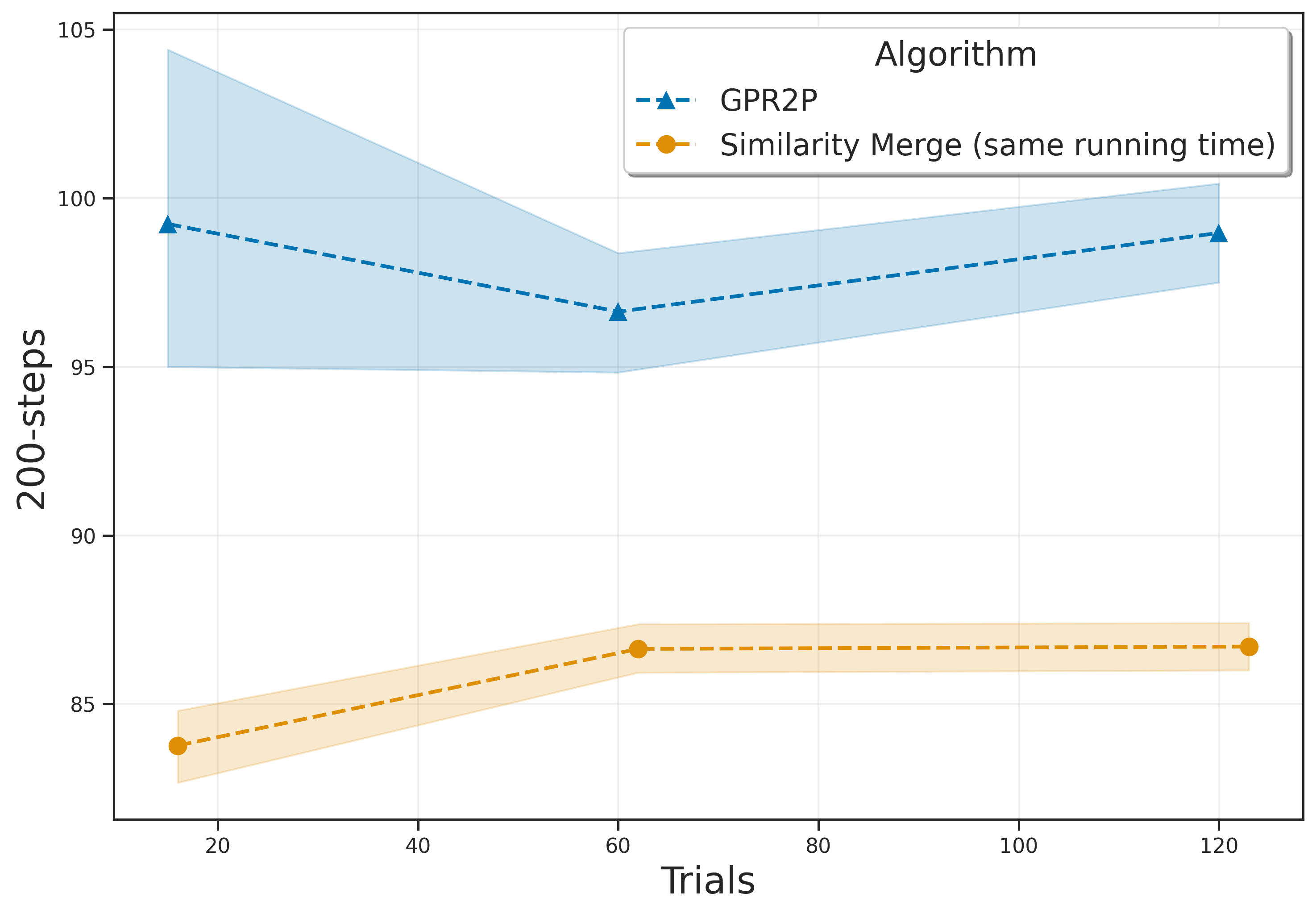
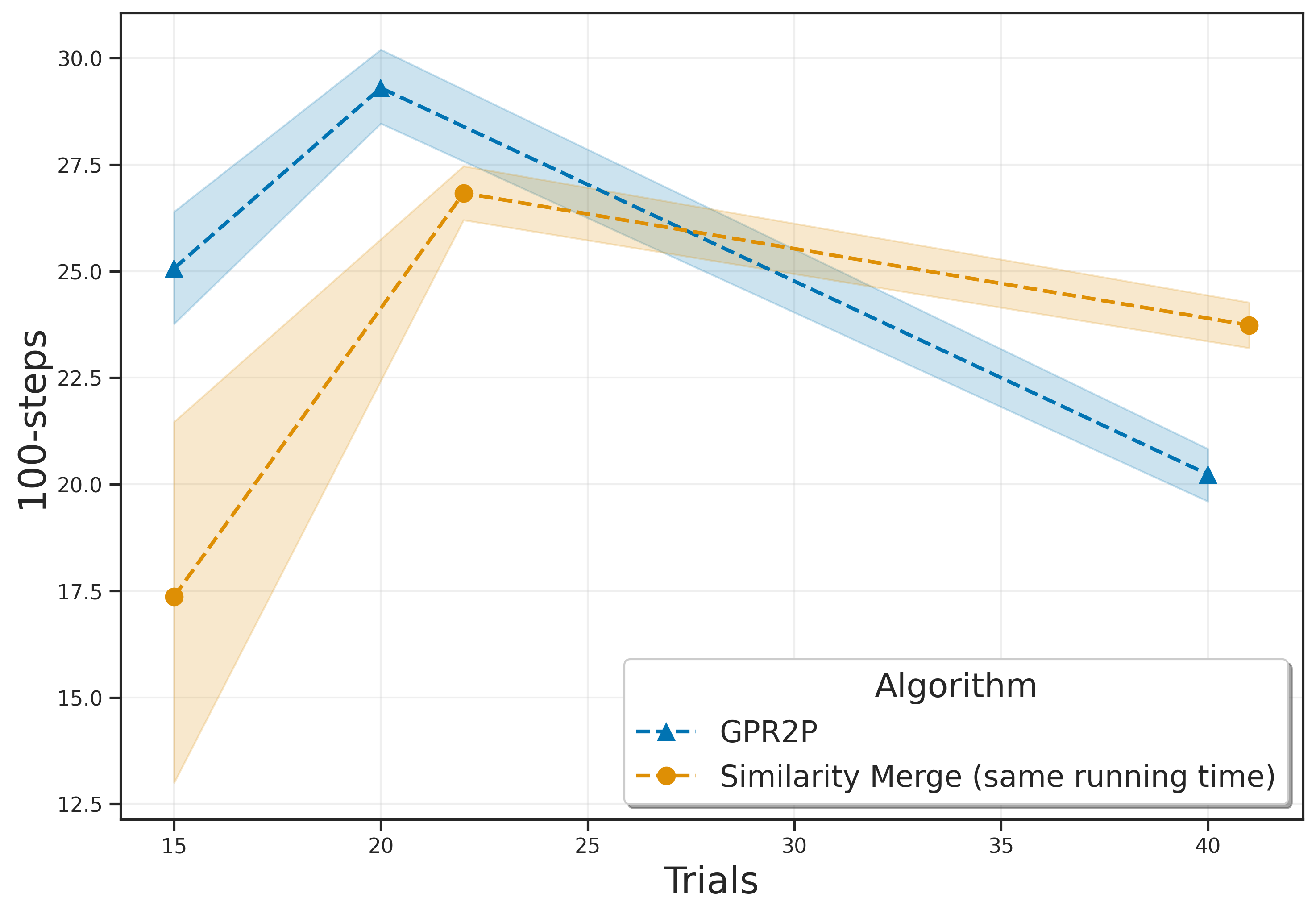
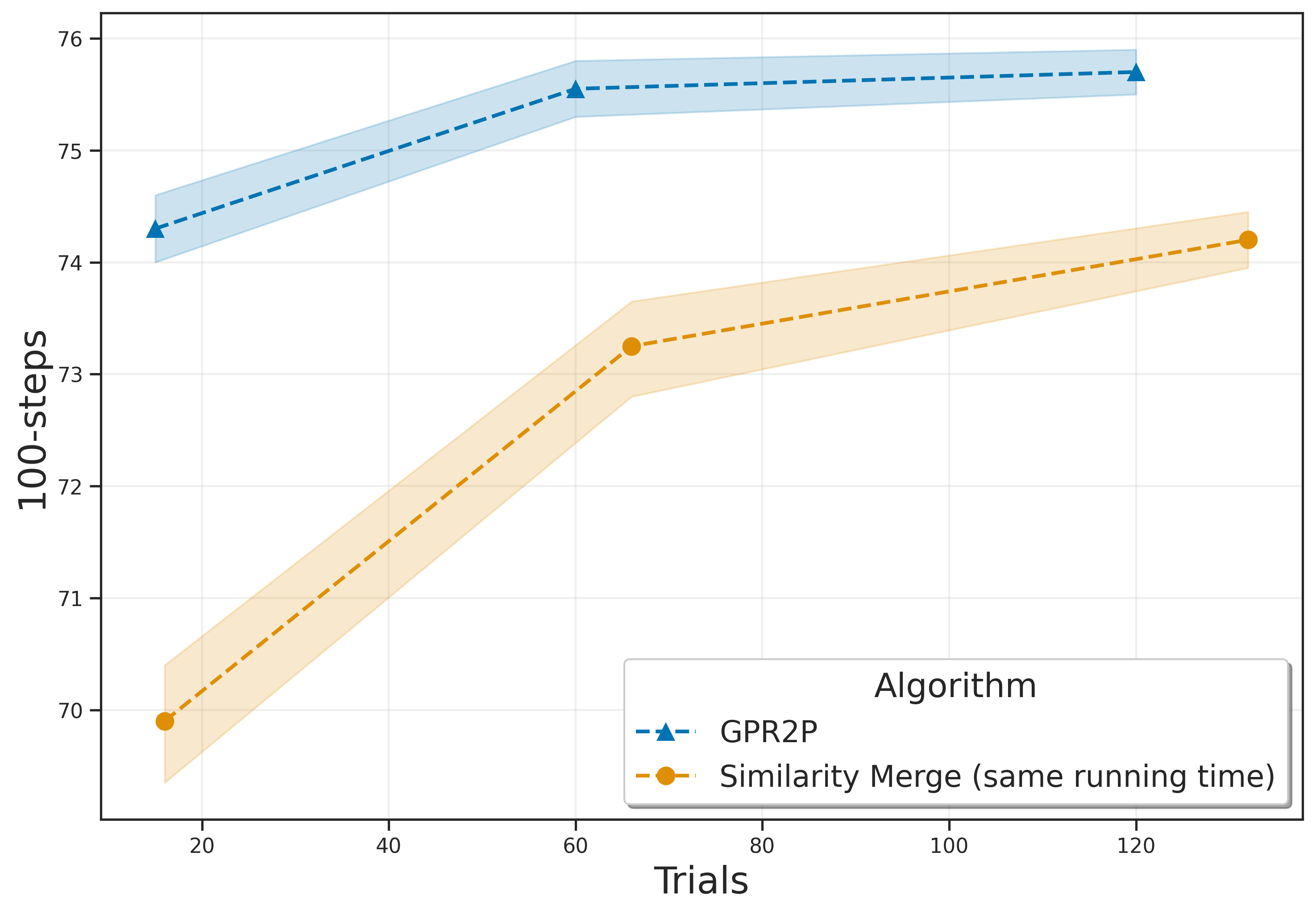
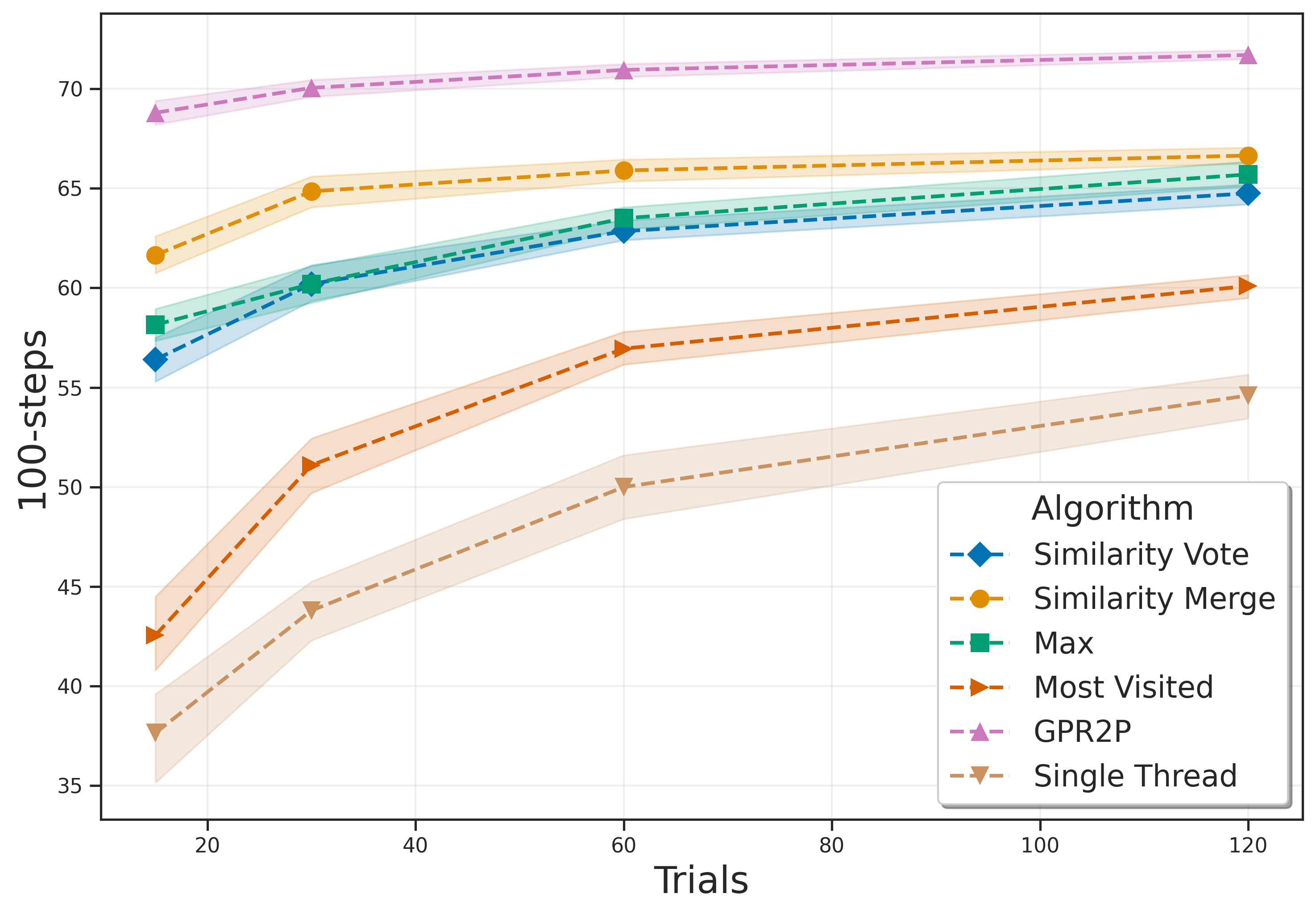
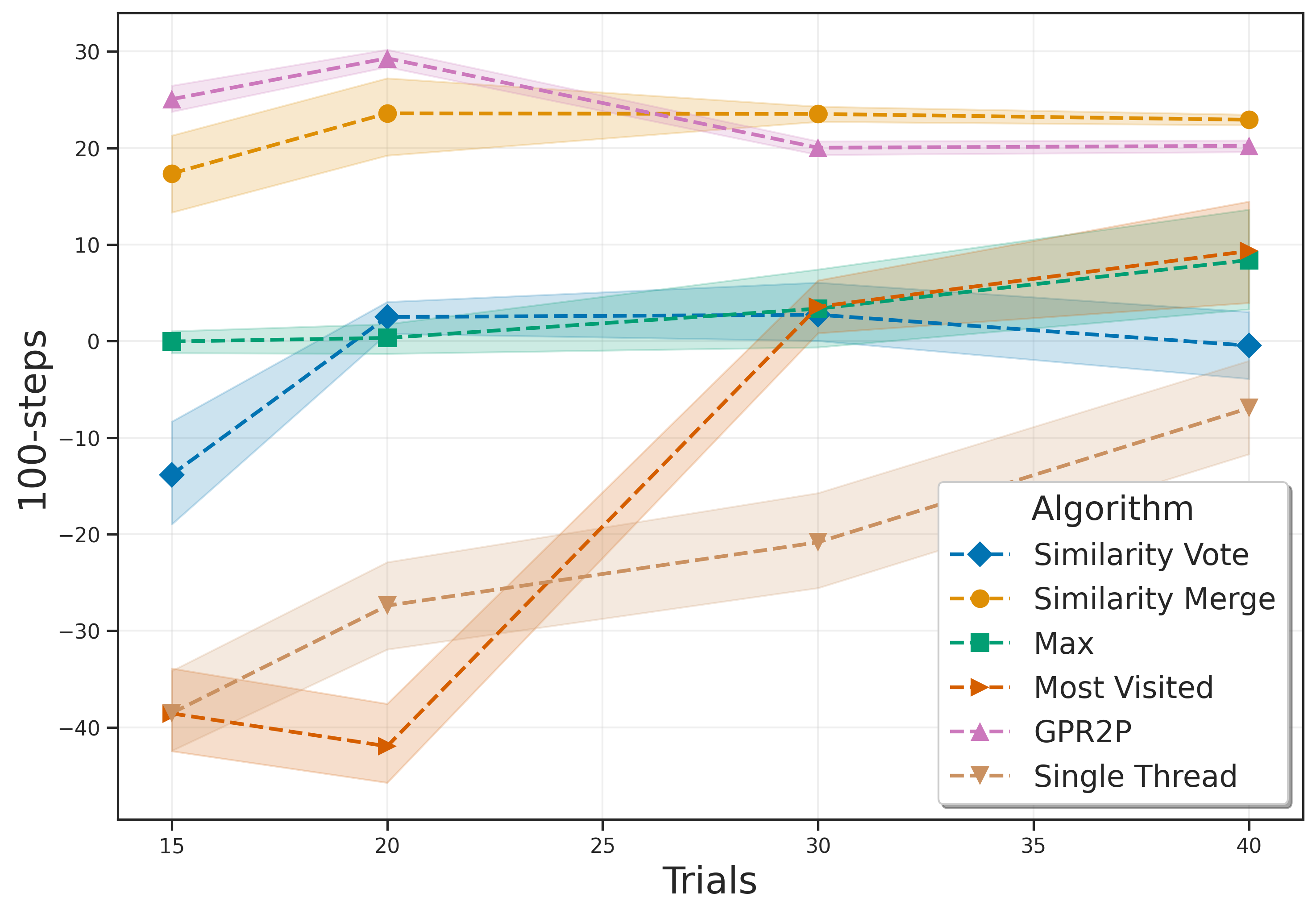
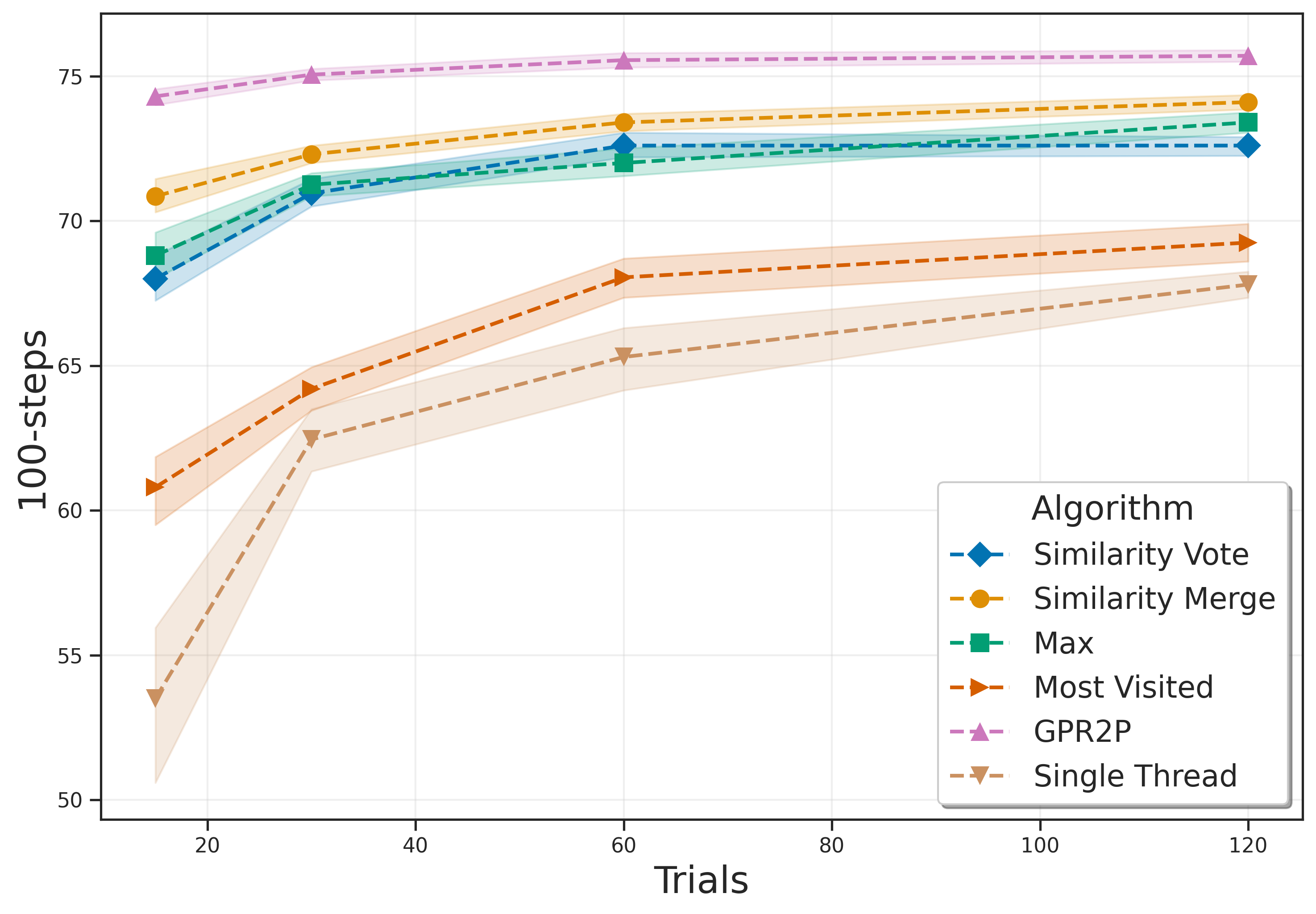
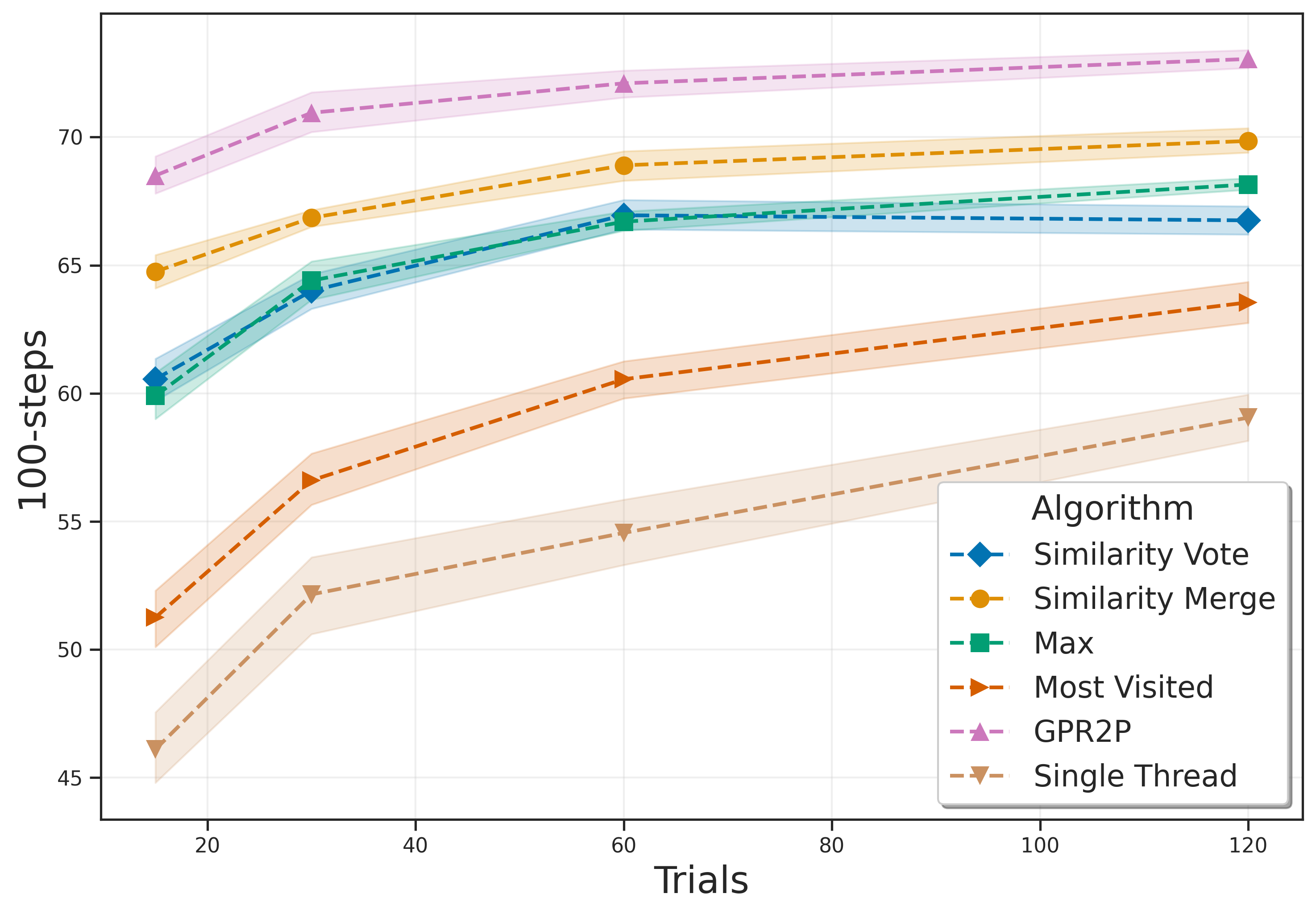
The contributions of our paper therefore aim to address these limitations: 1. We propose Gaussian Process Regression for Root Parallel MCTS (GPR2P). Unlike previous approaches that select only sampled actions, we construct a principled statistical model of the return over the entire action space. This capability is especially important when promising actions are difficult to sample and only a limited number of simulations can be performed. 2. We carry out a comprehensive empirical evaluation comparing GPR2P to previous techniques across six different environments, demonstrating that it yields better performance across the board while requiring a modest increase in inference time. To our knowledge, this also represents the most extensive evaluation of aggregation strategies for root-parallel MCTS in continuous domains to date.
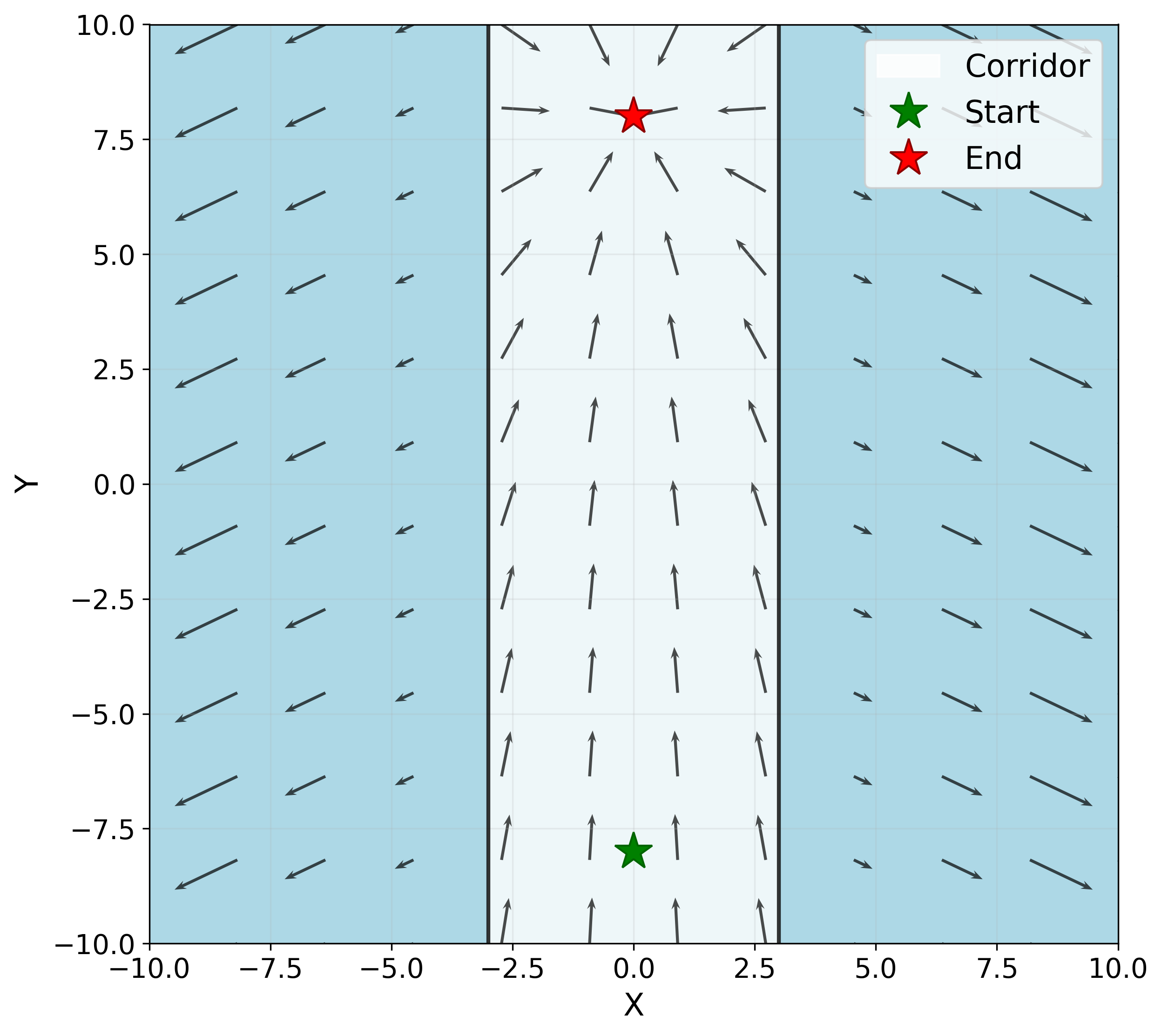
In this work, we consider an agent interacting with an environment under uncertain dynamics. This problem can be described as a Markov Decision Process (MDP) (Bellman 1957), which is formally defined by a tuple ⟨S, A, T, R, γ⟩ where (i) S ⊆ R N is the N-dimensional state space; (ii) A ⊆ R D is the D-dimensional action space; (iii) T (s, a, s ′ ) is the transition function, which represents the probability of reaching s ′ from s by taking action a; (iv) R is the reward function R(s, a) governing the reward received when taking action a in state s; (v) γ ∈ [0, 1] is the discount factor.
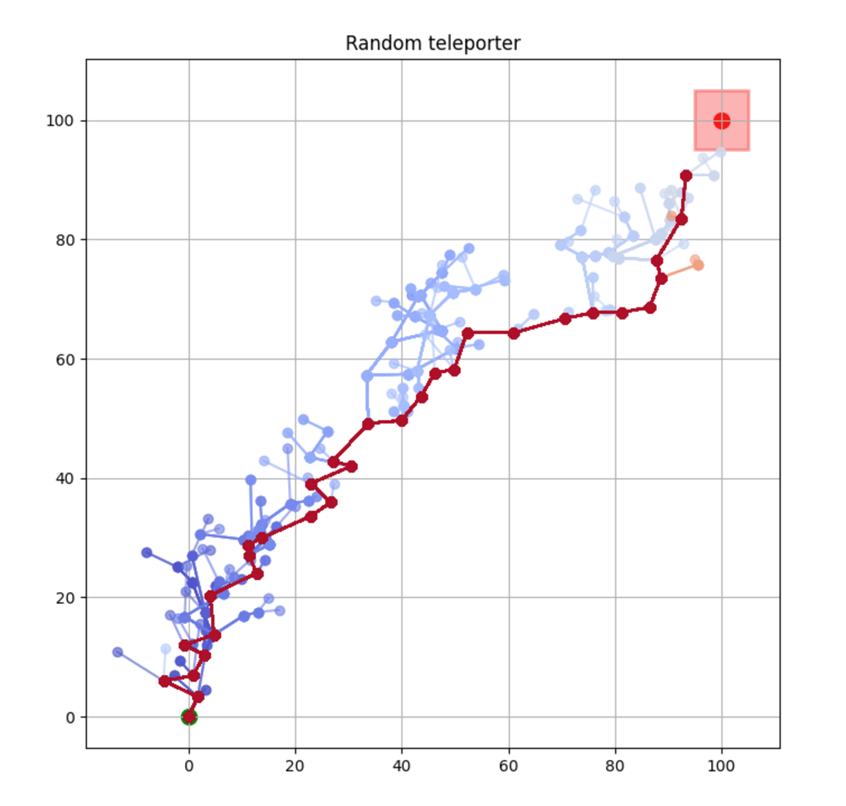
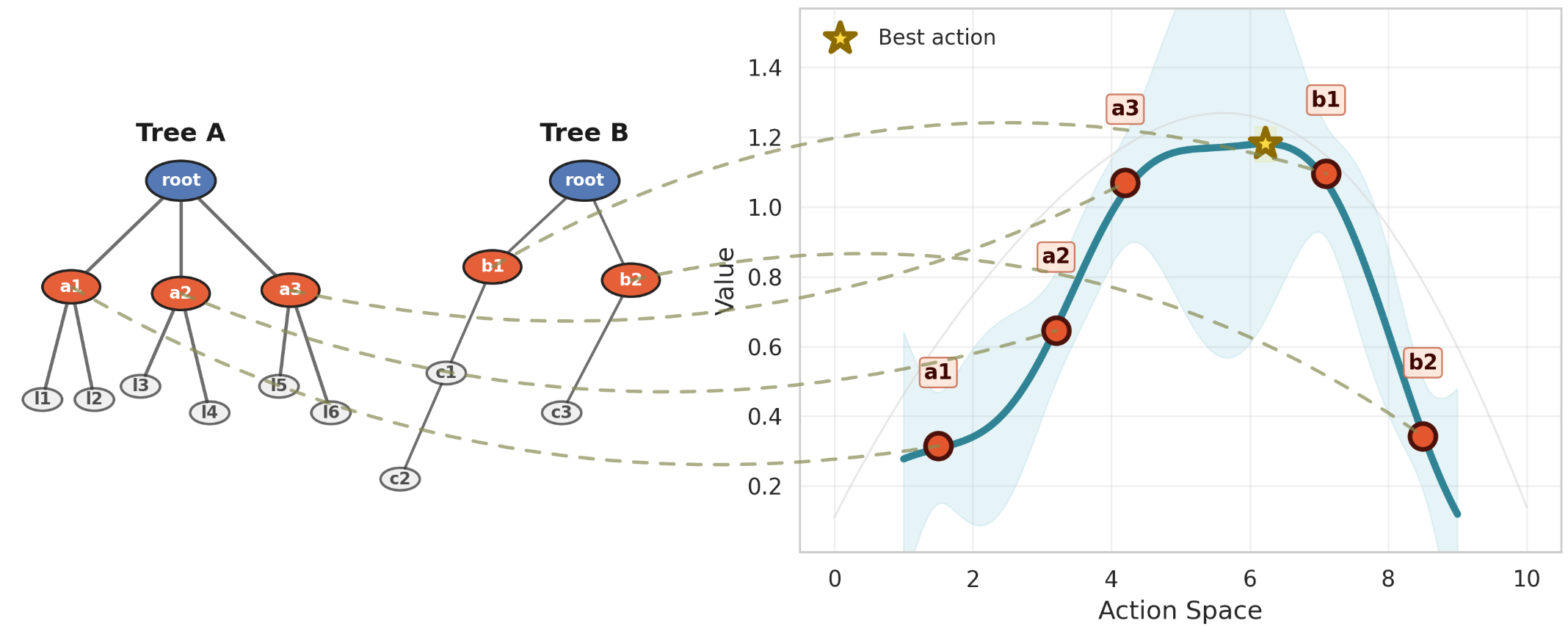
Figure 1: Illustration of the GPR2P method, which uses Gaussian Process Regression to perform aggregation in root-parallel MCTS. Unlike existing methods, GPR2P can estimate the return for and select actions that were not sampled in the tree.
In MDPs, a policy π maps states to actions, and its value function V π (s) denotes the expected sum of discounted rewards obtained by starting from state s and following π. The expected discounted reward from time t = 0 to time t = T is calculated as T t=0 γ t r t , where r t denotes the reward received at time t. There exists at least one optimal policy π * which optimizes the value function V π (s), ∀s ∈ S.
Monte Carlo Tree Search (MCTS) is a best-first search algorithm (Chaslot, Winands, and van Den Herik 2008) that performs randomized explorations in the search space and asymptotically converges to the optimal solution, which corresponds to the optimal trajectory in a Markov Decision Process (MDP). The search process is guided by selection strategies designed to balance the trade-off between exploring new actions (exploration) and exploiting promising ones based on existing samples (exploitation) (Browne et al. 2012). Among these strategies, the Upper Confidence Bounds for Trees (UCT) algorithm (Kocsis and Szepesvári 2006) is one of the most widely adopted, and it a
This content is AI-processed based on open access ArXiv data.