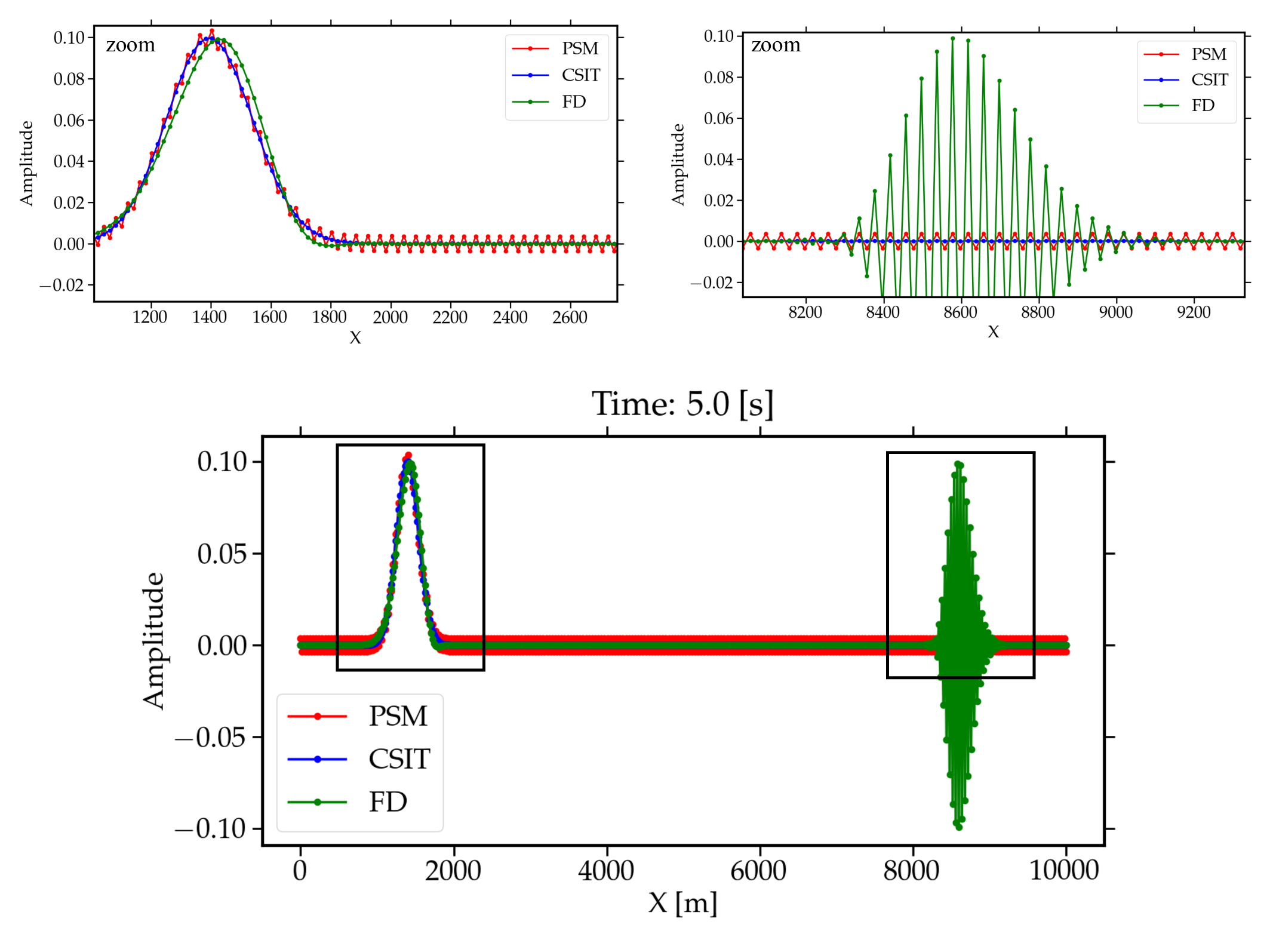
Building on the well-established connection between the Hilbert transform and derivative operators, and motivated by recent developments in complex-step differentiation, we introduce the Complex-Step Integral Transform (CSIT): a generalized integral transform that combines analytic continuation, derivative approximation, and multi-scale smoothing within a unified framework. A spectral analysis shows that the CSIT preserves phase while suppressing high-wavenumber noise, offering advantages over conventional Fourier derivatives. We discuss the roles of the real and imaginary step parameters, compare FFT-based and interpolation-based implementations, and demonstrate the method on the advection equation and instantaneous-frequency computation. Results show that the CSIT yields smoother, more robust attributes than Hilbert-based methods and provides built-in stabilization for PDE solvers. The CSIT thus represents a flexible alternative for numerical differentiation, spectral analysis, and seismic signal processing. The method opens several avenues for future work, including non-periodic implementations, adaptive parameter selection, and integration with local interpolation frameworks such as high-order Finite-Element methods.
Integral transforms are central mathematical tools across the physical sciences, providing systematic ways to recast functions into alternative domains where structure, oscillations, and scaling behavior become more transparent. Classical transforms such as the Fourier, Laplace, Radon, and Hilbert transforms underpin a wide range of techniques in signal analysis, inverse problems, and the study of differential equations.
Within seismology, integral transforms are especially valuable because they allow recorded wavefields-often nonstationary, multicomponent, and noisy-to be analyzed in representations that emphasize their physical content. Among these, the Fourier and Hilbert transforms are arguably the most widely used (Bracewell and Bracewell, 1986;Feldman, 2011). The Fourier transform enables spectral analysis, filtering, and the formulation of elastodynamic problems in the wavenumber domain (Bracewell and Bracewell, 1986;Slawinski, 2010), while the Hilbert transform is fundamental for constructing analytic signals, computing instantaneous amplitude and phase, and deriving seismic envelopes (e.g. Feldman, 2011;Bowman and Lees, 2013;Shen and Albertin, 2015).
Mathematically, many integral transforms share advantageous properties-linearity, convolution/multiplication dualities, and in many cases analytic continuation-which make them powerful for both theoretical manipulation and efficient numerical implementation (e.g., via the FFT). Practically, however, each transform brings trade-offs: periodicity assumptions, edge effects, sampling and aliasing, and sensitivity to noise must be managed through padding, tapering, filtering or alternative bases (e.g. nonperiodic Chebyshev or localized wavelet bases). These considerations motivate the development of generalized transforms and regularized spectral operators that combine analytic continuation, derivative estimation and multi-scale smoothing for robust seismic attribute extraction.
Several generalizations of the Hilbert transform, such as the fractional, bilinear and trilinear Hilbert transforms are active areas of research (e.g. Tao et al., 2008;Nabighian and Hansen, 2001;Lohmann et al., 1996;Venkitaraman and Seelamantula, 2014;Cruz-Uribe and Martell, 2018). These generalizations are applied to problems that range from mechanical vibrations (Feldman, 2011) to telecommunications (King, 2009) and they are also used in the Earth Sciences to illuminate faults and channels embedded in 3D seismic data (Luo et al., 2003), to achieve better noise robustness and higher resolution results to capture subtle geologic features (Zhang et al., 2019), for automatic interpretation of potential field data (Nabighian, 1984). Also, combining the Hilbert transform with the first and/or second derivative operators has been used to enhance the detection of seismic waves generated in the deep Earth (Chambers et al., 2005;Saki et al., 2019;Ibourichene and Romanowicz, 2018).
The most common expression for the Hilbert transform is given by the following equation (King, 2009)
where u(t) is the function, of parameter t, to be transformed. Eq. ( 1) can be understood as the convolution of the function u(t) with the function 1/(πt). With a simple change of variables we can write the Hilbert transform (eq. ( 1)) as follows (Zygmund, 2002)
One can note that the term inside the integral has the mathematical structure of the centered finite-difference (FD) approximation for the first-order derivative given by the following expression (Thomas, 1995;Cohen, 2002;Trefethen, 1996;Strikwerda, 2004;Moczo et al., 2014)
where ∆x refers to an increment in the x direction or grid spacing and O(∆x 2 ) to the error in the approximation. A generalization of the FD approximation eq. ( 3) is the complex-step (CS) approximation (Squire and Trapp, 1998) given by the following expression
where Im refers to the imaginary part and i 2 = -1. The CS approximation eq. ( 4) has proven to have several advantages over conventional FD techniques, mainly the numerical instabilities related to subtraction cancellation errors can be avoided (note the subtraction term in the numerator in eq. ( 3) is absent in eq. ( 4)) and higher-order accuracy at a single step (Abreu et al., 2015(Abreu et al., , 2013;;Anderson et al., 2001;Al-Mohy and Higham, 2010;Voorhees et al., 2011;Martins et al., 2001Martins et al., , 2003;;Dziatkiewicz, 2016;Jin et al., 2010;Kim et al., 2006;Burg and Newman, 2003;Wang and Apte, 2006;Ridout, 2009). Several generalizations to the initial CS derivative approximation (4) have been made (e.g. Lai and Crassidis (2008); Cerviño and Bewley (2003); Abokhodair (2009); Abreu et al. (2013); Ibrahim and Jalab (2013); Hürkamp et al. (2015); Lantoine et al. (2012)). A simple generalization made by Abreu et al. (2013) consisted into taking a complex step (h + iv) in a strict sense in the original CS approximation (4) as follows
where h, v ∈ R and h, v → 0. Although discretization eq. ( 5) is less accurate com
This content is AI-processed based on open access ArXiv data.