$\renewcommand{\Re}{\mathbb{R}}$We present a new optimal construction of a semi-separated pair decomposition (i.e., SSPD) for a set of $n$ points in $\Re^d$. In the new construction each point participates in a few pairs, and it extends easily to spaces with low doubling dimension. This is the first optimal construction with these properties.
As an application of the new construction, for a fixed $t>1$, we present a new construction of a $t$-spanner with $O(n)$ edges and maximum degree $O(\log^2 n)$ that has a separator of size $O\pth{n^{1-1/d}}$.
For a point-set P, a pair decomposition of P is a set W of pairs of subsets of P, such that for every pair of points of p, q ∈ P there exists a pair {X , Y} ∈ W such that p ∈ X and q ∈ Y-see Section 2 for the formal definition. A well-separated pair decomposition (WSPD) of P is a pair decomposition of P such that for every pair {X , Y}, the distance between X and Y is large when compared to the maximum diameter of the two point sets. The notion of WSPD was developed by Callahan and Kosaraju [ CK95 ], and it provides a compact representation of the quadratic pairwise distances of the point-set P, since there is a WSPD with a linear number of pairs.
The total weight of a pair decomposition W is the total size of the sets involved; that is ω(W) = {X ,Y}∈W (|X | + |Y|). Naturally, a WSPD with near linear weight is easier to manipulate and can be used in applications where the total weight effects the overall performance. Unfortunately, it is easy to see that, in the worst case, the total weight of any WSPD is Ω(n 2 ). Callahan and Kosaraju [ CK95 ] overcame this issue by generating an implicit representation of the WSPD using a tree. Indeed, they build a tree T (usually a compressed quadtree, or some other variant) that stores the points of the given point set in the leaves. Pairs are reported as {u, v} where u and v are nodes in the tree such that their respective pair S(u) ⊗ S(v) is well separated, where S(u) denotes the set of points stored at the subtree of u.
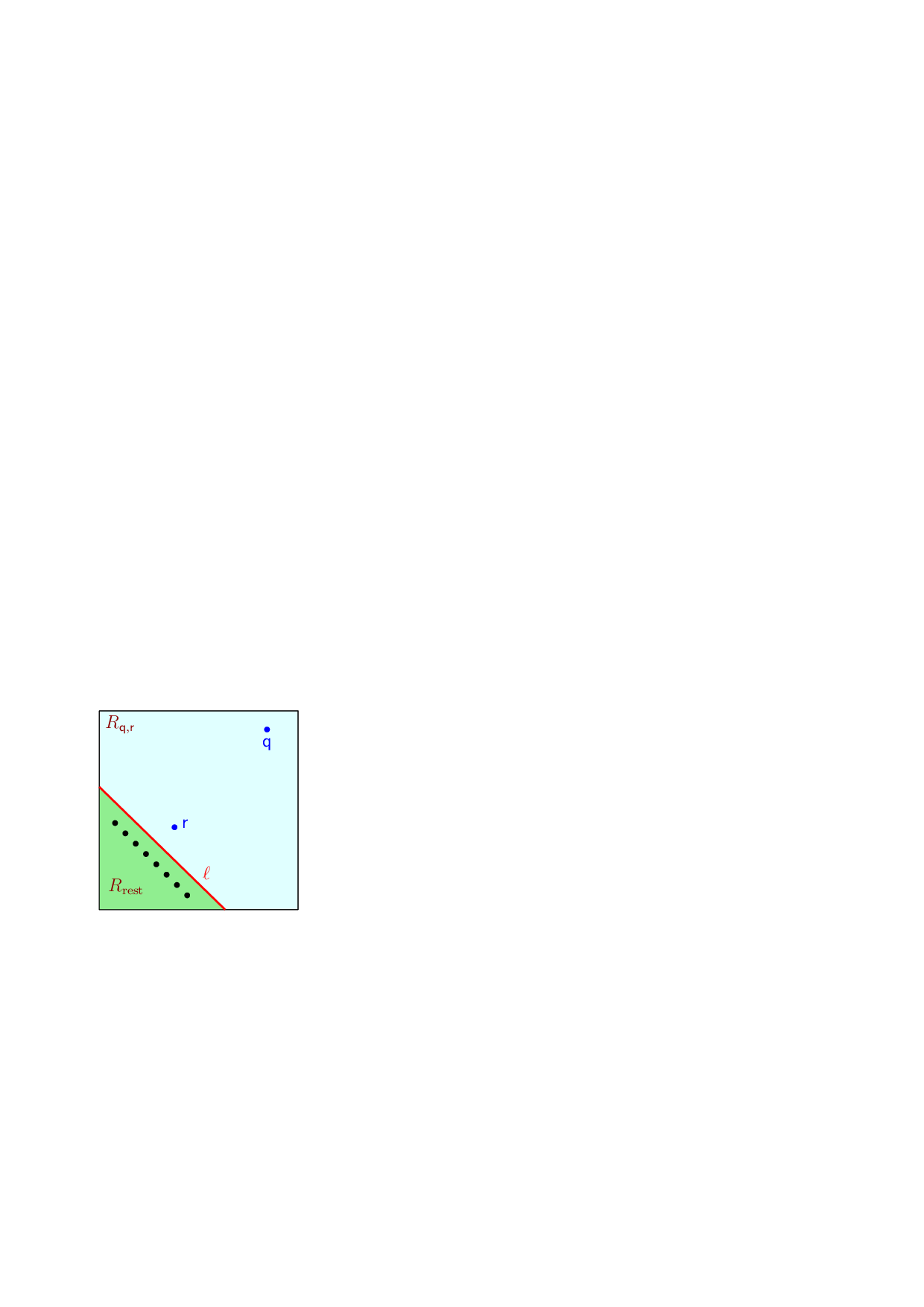
SSPDs. To overcome this obesity problem, a weaker notion of semi-separated pair decomposition (SSPD) had been suggested by Varadarajan [ Var98 ]. Here, an SSPD S of a point set has the property that for each pair {X , Y} ∈ S the distance between X and Y is large when compared to the minimum diameter of the two point sets (in the WSPD case this was the maximum of the diameters). See Figure 1.1 for an example of a semi-separated pair that is not well-separated. By weakening the separation, one can get an SSPD with near-linear total weight. Specifically, Varadarajan [ Var98 ] showed how to compute an SSPD of weight O n log 4 n for a set of n points in the plane, in O(n log 5 n) time (for a constant separation factor). He used the SSPD for speeding up his algorithm for the min-cost perfect-matching in the plane. Recently, Abam et al. [ ABFG09 ] presented an algorithm which improves the construction time to O(ε -2 n log n) and the weight to O(ε -2 n log n), where 1/ε is the separation required between pairs. It is known that any pair decomposition has weight Ω(n log n) [ BS07 ], implying that the result of Abam et al. [ ABFG09 ] is optimal. This construction was generalized to R d with the construction time being O(ε -d n log n) and the total weight of the SSPD being O(ε -d n log n), see [ ABF+11 ].
Spanners. More recently SSPDs were used in constructing certain geometric spanners [ ABFG09 ,ABF+11 ,ACFS09 ]. Let G = (P, E) be a geometric graph on a set P of n points in R d . That is, G is an edge-weighted graph where the weight of an edge pq ∈ E is the Euclidean distance between p and q. The distance in G between two points p and q, denoted by d G (p, q), is the length of the shortest (that is, minimum-weight) path between p and q in G. A graph G is a (geometric) t-spanner , for some t ≥ 1, if for any two points p, q ∈ P we have d G (p, q) ≤ t • ∥pq∥. Note that the concept of geometric spanners can be easily extended to any metric space. Geometric spanners have received considerable attention in the past few years-see [ NS07 ] and references therein. Obviously, the complete graph is a t-spanner, but a preferable spanner would provide short paths between its nodes, while having few edges. Other properties considered include (i) low total length of edges, (ii) low diameter, (iii) low maximum degree, and (iv) having small separators.
Separators. A graph G is said to have a k-separator if its vertices can be decomposed into three sets X , Y and Z such that both |X | and |Y| are Ω(n) and |Z| ≤ k (i.e., the set Z is the separator ). Furthermore, there is no edge in G connecting a vertex in X to a vertex in Y. Graphs with good separators are the best candidates to applying the divide and conquer approach-see [ LT80 , MTTV97 , SW98 ] and references therein for more results and applications. Lipton and Tarjan [ LT80 ] showed that any planar graph has an O √ n -separator. The Delaunay triangulation of a planar point-set P is an
. Furthermore, it is a planar graph and is thus an O(1)-spanner with an O( √ n)separator. Fürer and Kasiviswanathan [ FK07 ] recently presented a t-spanner for a ball graph which is an intersection graph of a set of n ball in R d with arbitrary radii which has an O n 1-1/d -separator. Since complete Euclidean graphs are a special case of unit ball graphs, their results yields a new construction of t-spanner for geometric graphs with small separators.
Metric spaces with low doubling dimension. Recently the notion of doubling dimension [
This content is AI-processed based on open access ArXiv data.