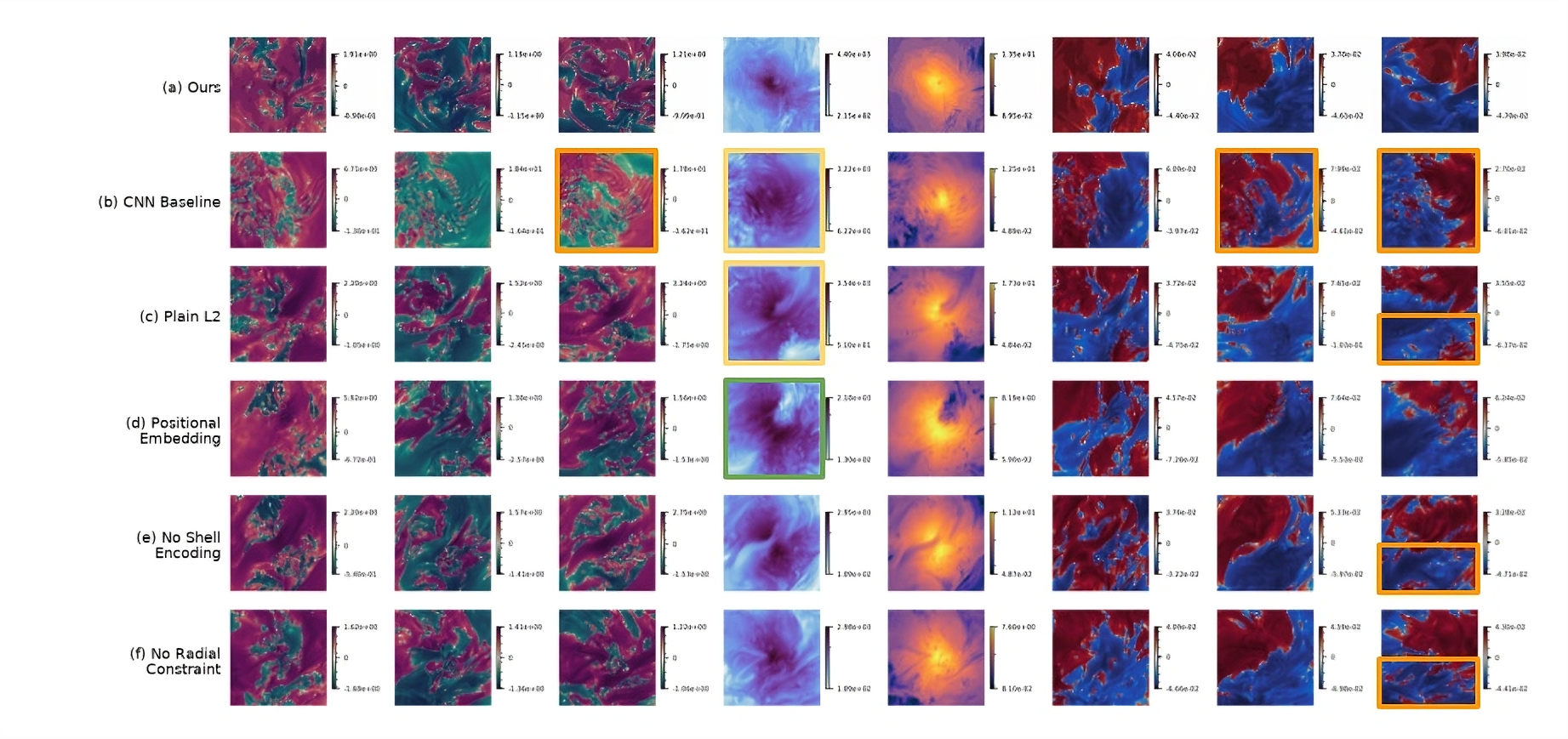
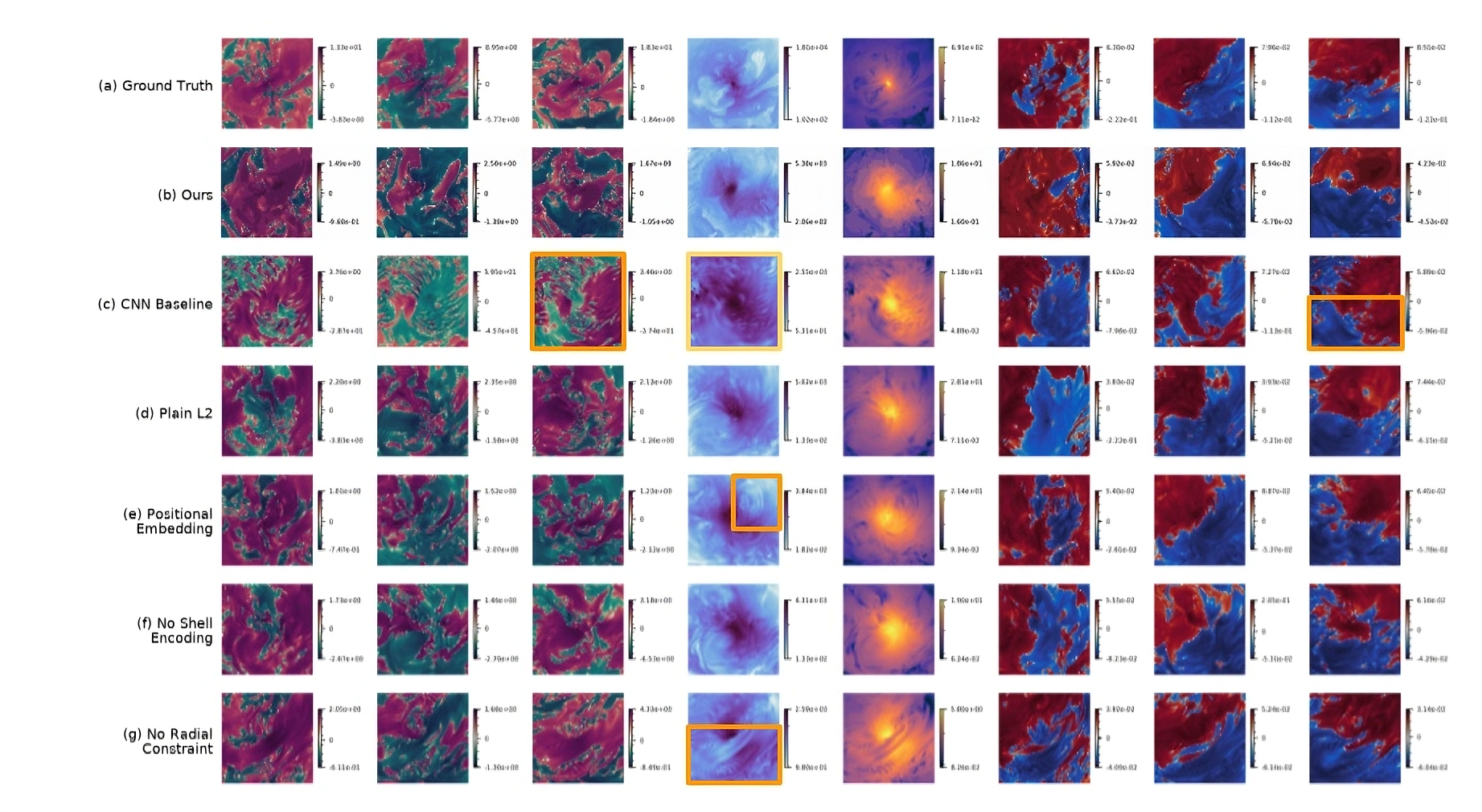
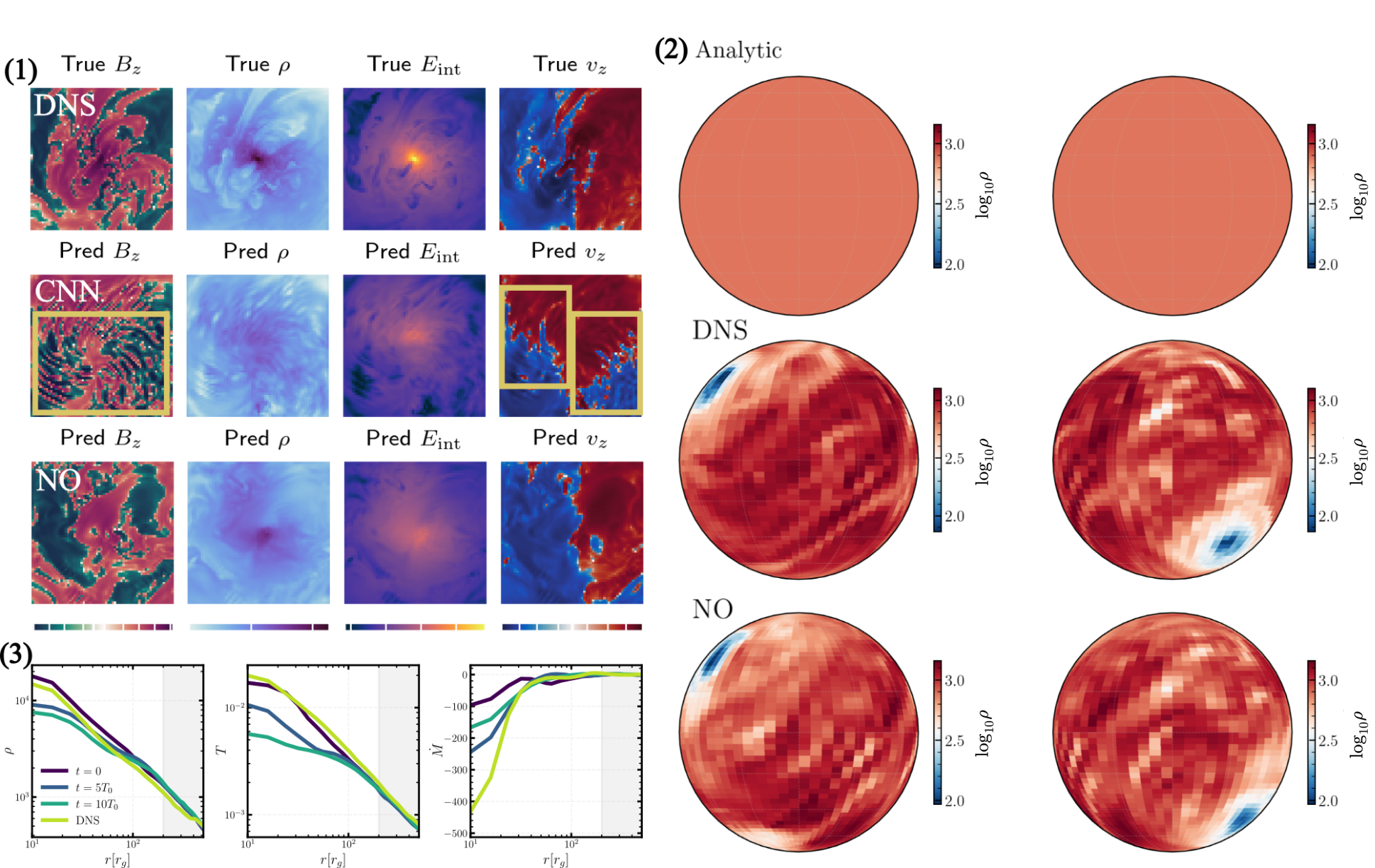
Modeling how supermassive black holes co-evolve with their host galaxies is notoriously hard because the relevant physics spans nine orders of magnitude in scale-from milliparsecs to megaparsecs--making end-to-end first-principles simulation infeasible. To characterize the feedback from the small scales, existing methods employ a static subgrid scheme or one based on theoretical guesses, which usually struggle to capture the time variability and derive physically faithful results. Neural operators are a class of machine learning models that achieve significant speed-up in simulating complex dynamics. We introduce a neural-operator-based ''subgrid black hole'' that learns the small-scale local dynamics and embeds it within the direct multi-level simulations. Trained on small-domain (general relativistic) magnetohydrodynamic data, the model predicts the unresolved dynamics needed to supply boundary conditions and fluxes at coarser levels across timesteps, enabling stable long-horizon rollouts without hand-crafted closures. Thanks to the great speedup in fine-scale evolution, our approach for the first time captures intrinsic variability in accretion-driven feedback, allowing dynamic coupling between the central black hole and galaxy-scale gas. This work reframes subgrid modeling in computational astrophysics with scale separation and provides a scalable path toward data-driven closures for a broad class of systems with central accretors.
Background. Supermassive black holes (SMBHs) co-evolve with their host galaxies through a twoway feeding-feedback loop that operates across nine orders of magnitude in scale [1]. Accretion flows near the event horizon (milliparsec scales) are governed by general relativistic magnetohydrodynamics (GRMHD) and launch relativistic jets and winds. These outflows propagate from AU to megaparsec scales, well beyond the host galaxy, depositing energy and momentum into the interstellar and intergalactic media [2,3]. The resulting feedback regulates star formation and galaxy growth, while galaxy-scale gas dynamics in turn modulate the inflow feeding the central black hole.
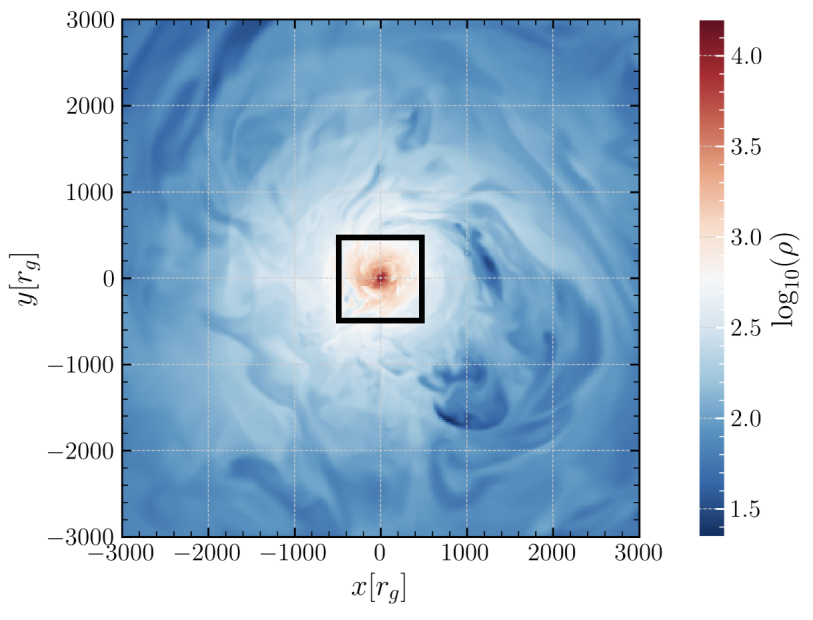
Challenge. This multiscale coupling makes end-to-end simulation computationally intractable: accurately resolving accretion flows demands timesteps set by the gravitational radius (r g ∼ mpc for M87), while capturing galaxy-scale feedback requires following dynamics over ∼ 10 9 times larger spatial and temporal scales. Bridging these domains requires passing information across many orders of magnitude in space and time without washing out variability or violating conservation.
Figure 1: Illustration of our method in a two-level setting. The neural operator efficiently replaces the evolution on small scales (zoom in), enabling proper feedback on large scale (zoom out).
A considerable amount of efforts adopting various techniques has been made to bridge different scales, including direct simulations under reduced scale separation [4][5][6][7], nested mesh “zoom-in” approaches in Eulerian codes [8,9], “Lagrangian hyper-refinement” in Larangian codes [10,11], remapping between domains [12], and iterative “multi-zone” [13][14][15] or “cyclic-zoom” [16] schemes that repeatedly refine/de-refine around the SMBH. Among these, multi-zone and cyclic-zoom methods propagate small-scale feedback to larger domains and evolve to consistency, but can still struggle with temporal variability and with specifying a physically faithful inner boundary (here we name this by subgrid black hole) across levels. The inner boundary adopted this way could feed erroneous information (e.g., in both methods, the relativistic jet cannot be turned on/off when crossing the boundary) to the active simulation domain, consequently alter the final results.
Neural Operator. Neural operators (NOs) represent a recent advance in machine learning for partial differential equations, learning mappings between infinite-dimensional function spaces rather than approximating individual functions [17,18]. This approach has demonstrated substantial computational acceleration and shown promise as surrogate models across various applications [19][20][21][22][23][24]. Recent studies have begun exploring NOs for coarse graining or closure modeling problems [23]. Astrophysical systems present unique challenges. Realistic galaxy formation involves large-scale, strongly coupled dynamics with central singularities at supermassive black holes, requiring stable long-term integration over cosmological timescales. The extreme dynamic range, combined with the inherent scarcity of training data in astrophysical simulations, creates a particularly demanding test case for NO or other machine learning methods. To the best of our knowledge, despite some preliminary attempts in simplified systems or transient-state predictions [25][26][27][28], no previous work has demonstrated NO performance in such complex, multi-scale systems with limited training data.
Contribution. We introduce a neural-operator-based “subgrid black hole” coupled to a direct multi-level solver, replacing hand-crafted closure rules with a data-driven model that captures realistic variability in accretion and feedback (see fig. 1 for a schematic illustration of our method):
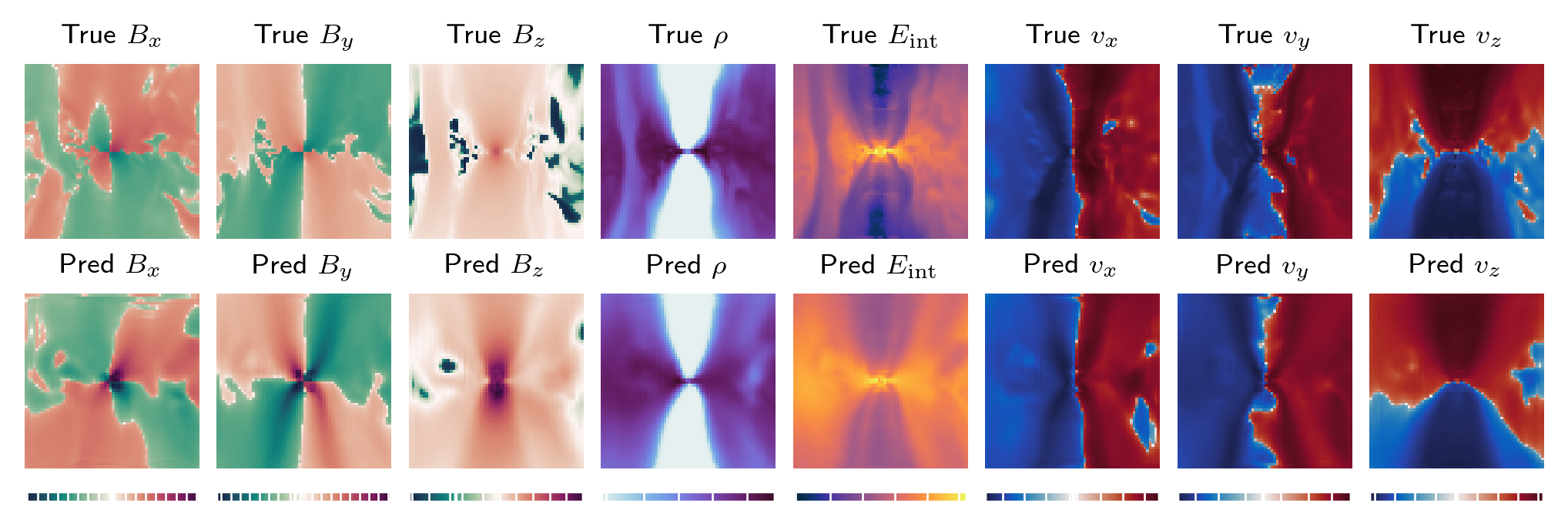
(1) Operator-learning subgrid. We train a neural operator to approximate the small-scale (GR)MHD time-evolution semigroup. The learned model supplies boundary conditions and fluxes to the next coarser level, enabling long-horizon rollouts without assuming steady or time-averaged injection. (2) Two-way multiscale coupling. Embedded within a multi-level framework, the learned subgrid responds to evolving large-scale conditions and, in turn, drives feedback that propagates outward-preserving variability critical to galaxy-SMBH co-evolution. (3) General applicability. The demonstrated approach is broadly applicable as a subgrid model for systems with a central accretor (e.g., SMBHs and neutron stars), independent of problem setups and generalizable to different codes. This work reframes subgrid modeling in computational astrophysics as operator learning: rather than prescribing fixed closures, we learn the small-scale dynamics to provide dynamically-updated boundary conditions for larger domains. This advance in subgrid modeling fills up the missing piece for the black hole accretion and feedback problem. More importantly, this could revolutionize the modeling of black hole fe
This content is AI-processed based on open access ArXiv data.