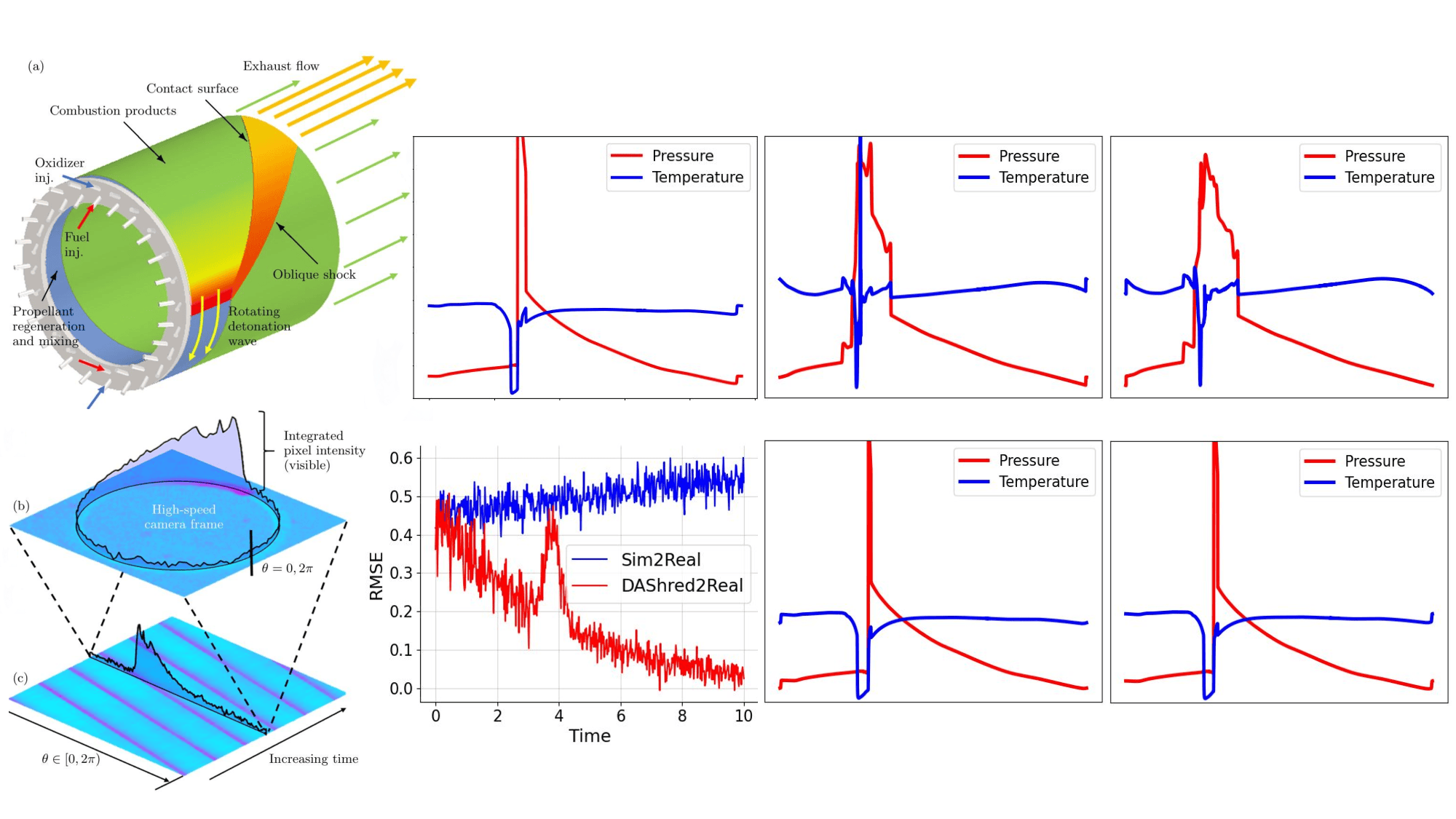
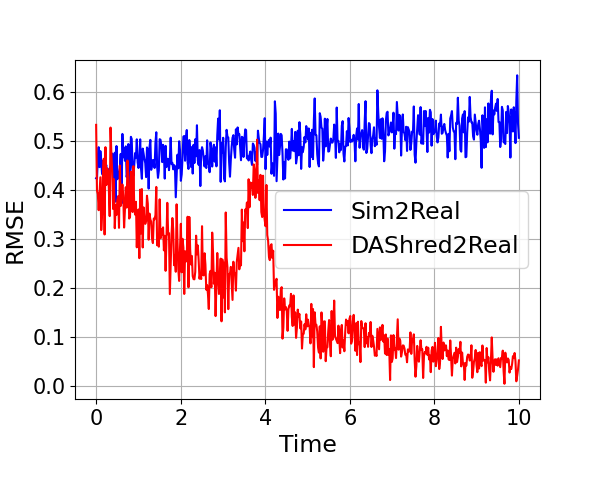
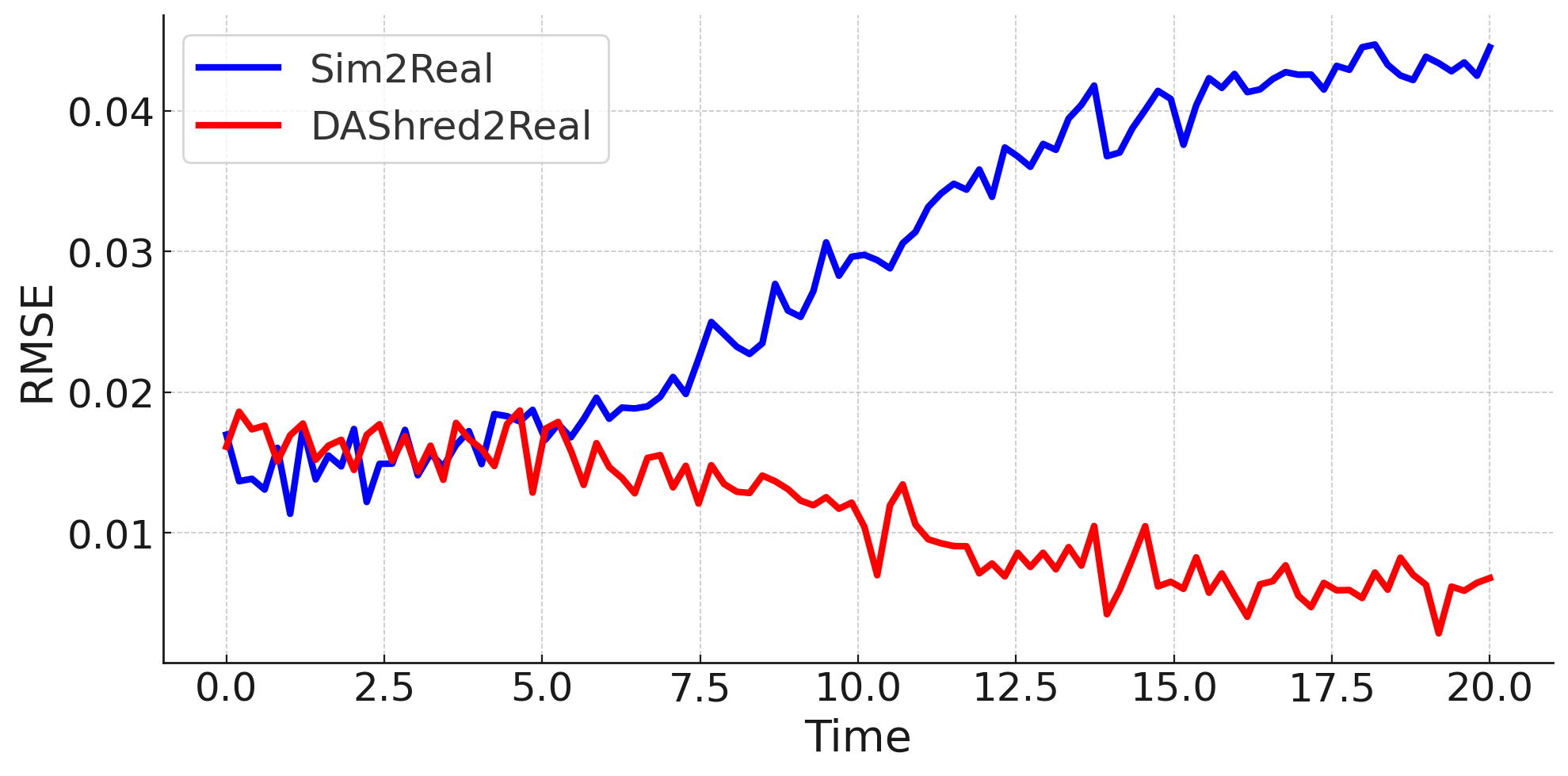
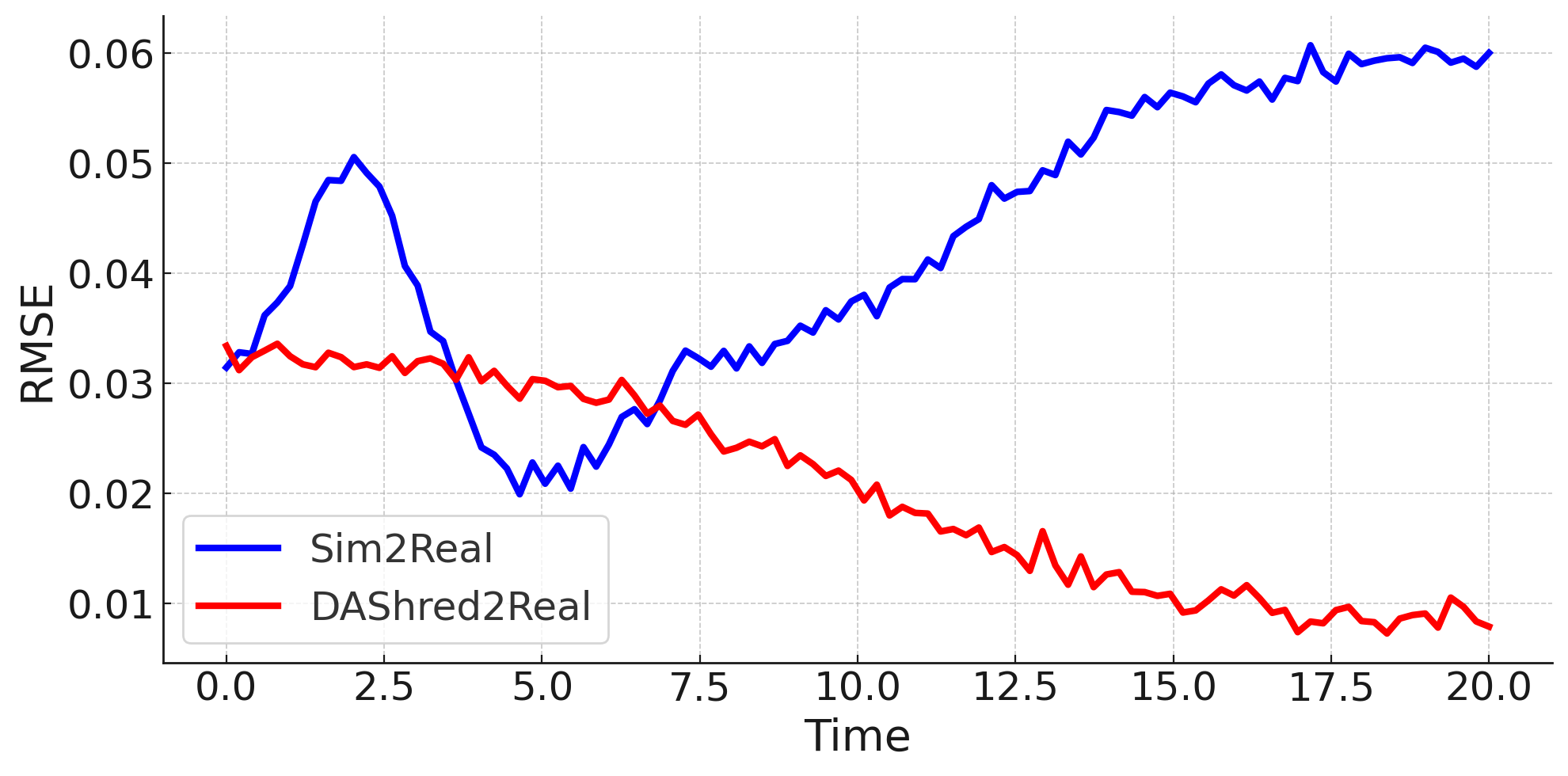
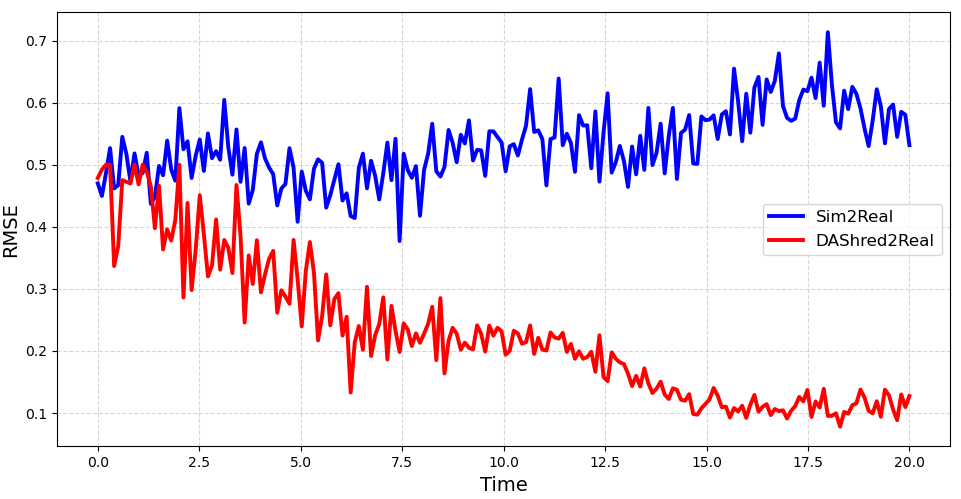
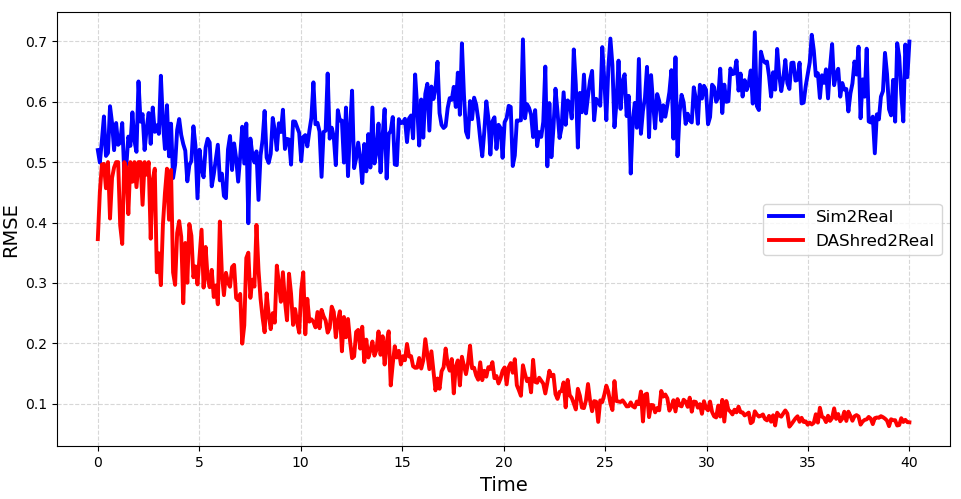
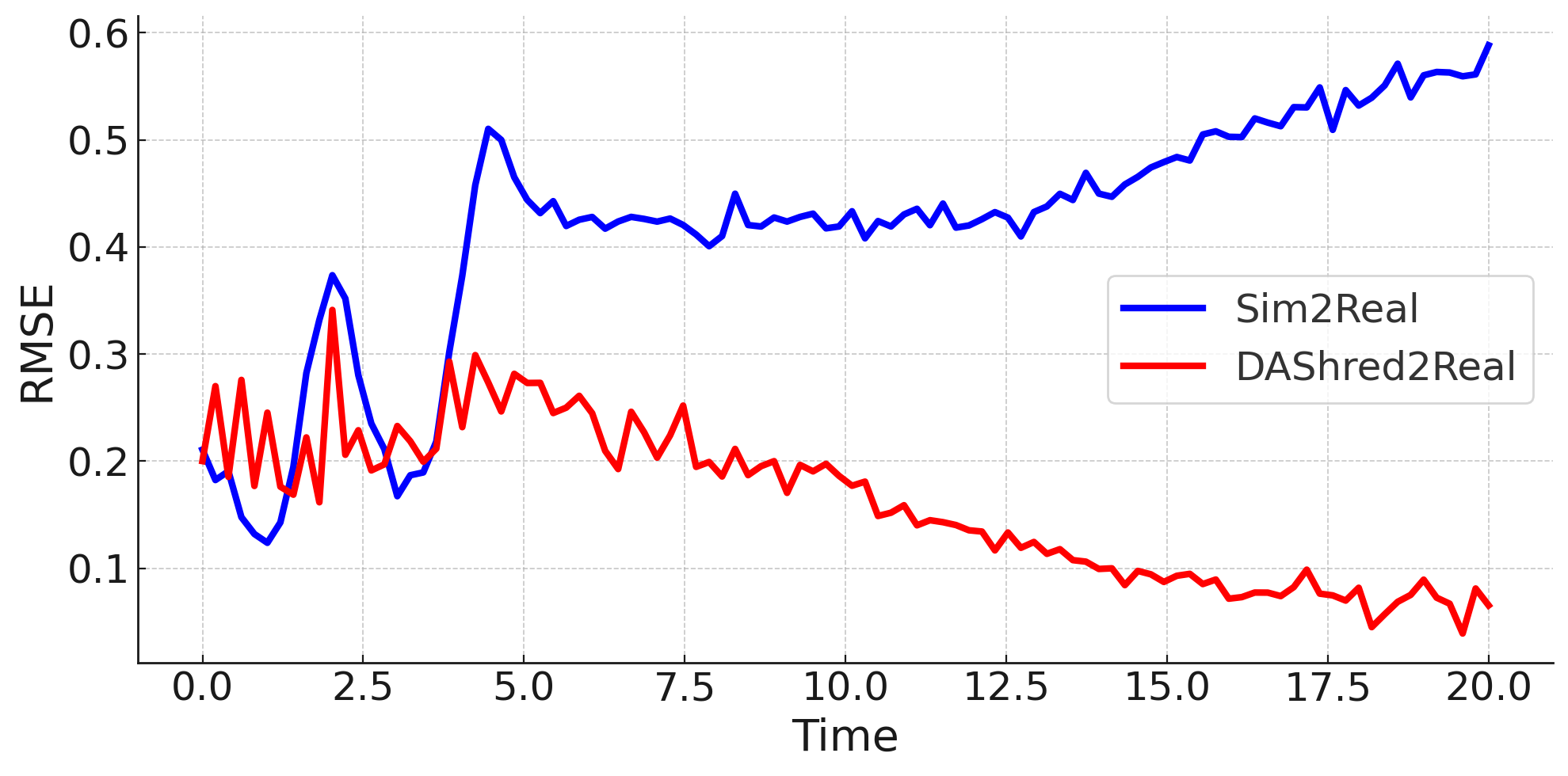
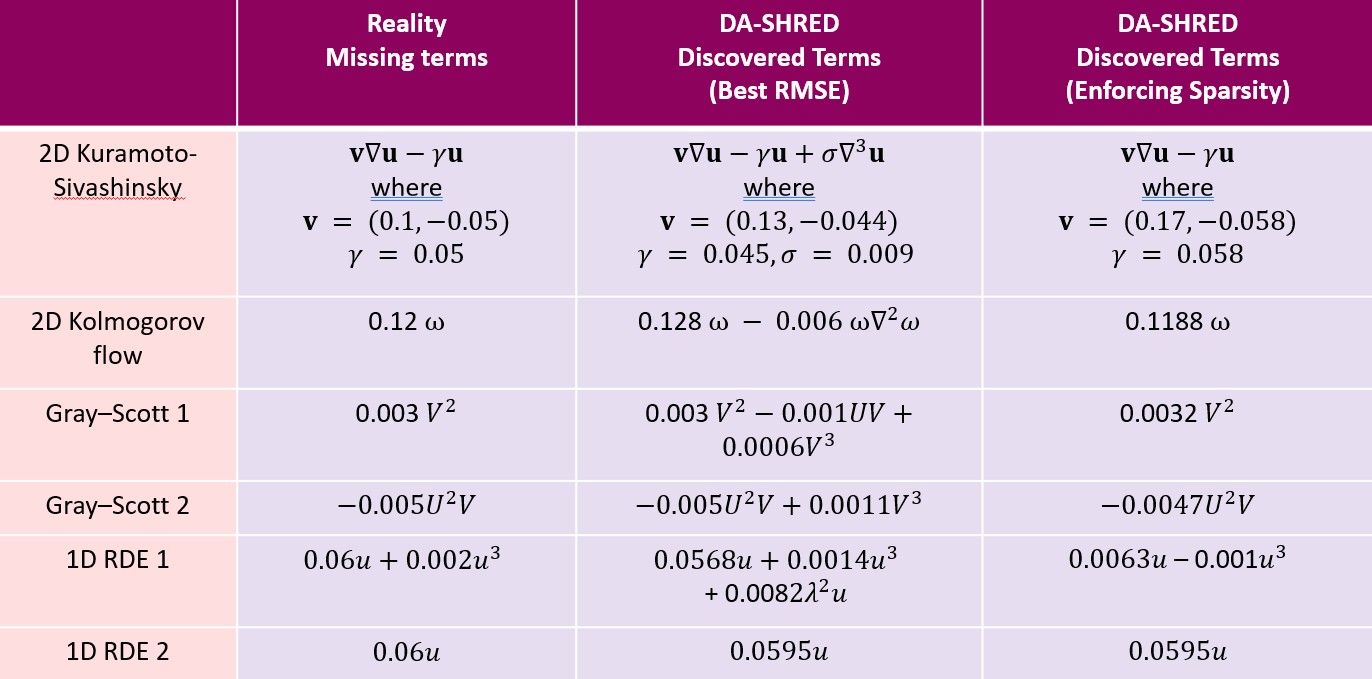
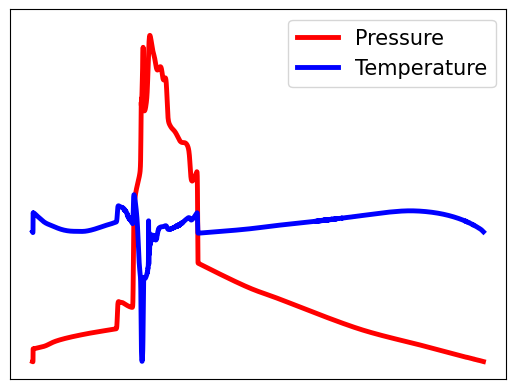
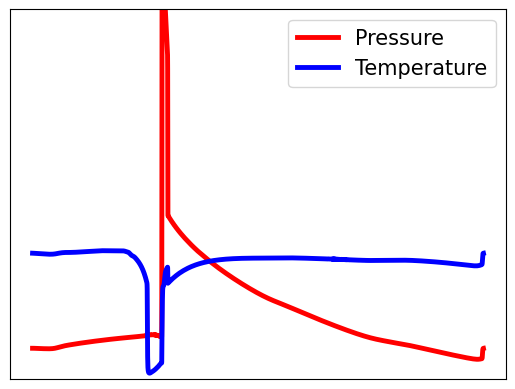
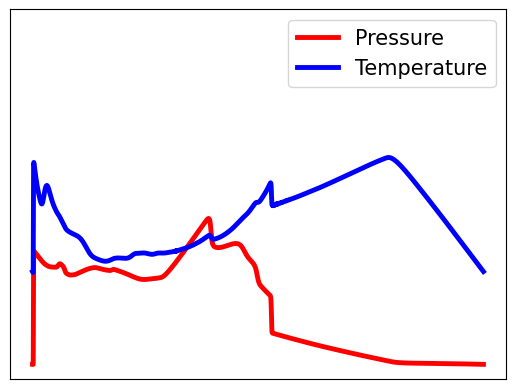
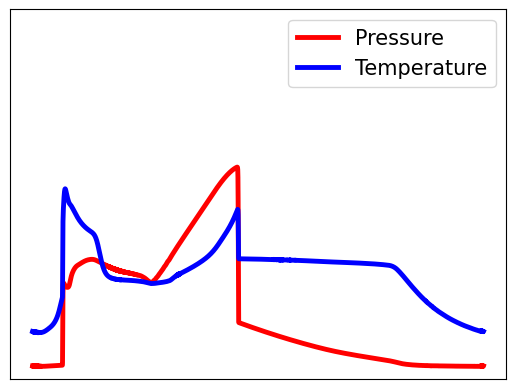
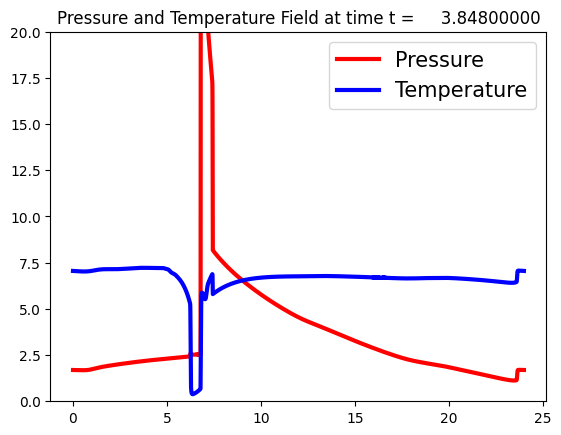
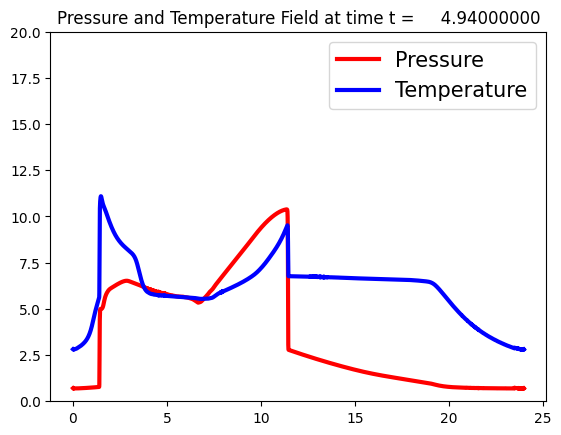
The requirements of modern sensing are rapidly evolving, driven by increasing demands for data efficiency, real-time processing, and deployment under limited sensing coverage. Complex physical systems are often characterized through the integration of a limited number of point sensors in combination with scientific computations which approximate the dominant, full-state dynamics. Simulation models, however, inevitably neglect small-scale or hidden processes, are sensitive to perturbations, or oversimplify parameter correlations, leading to reconstructions that often diverge from the reality measured by sensors. This creates a critical need for data assimilation, the process of integrating observational data with predictive simulation models to produce coherent and accurate estimates of the full state of complex physical systems. We propose a machine learning framework for Data Assimilation with a SHallow REcurrent Decoder (DA-SHRED) which bridges the simulation-to-real (SIM2REAL) gap between computational modeling and experimental sensor data. For real-world physics systems modeling high-dimensional spatiotemporal fields, where the full state cannot be directly observed and must be inferred from sparse sensor measurements, we leverage the latent space learned from a reduced simulation model via SHRED, and update these latent variables using real sensor data to accurately reconstruct the full system state. Furthermore, our algorithm incorporates a sparse identification of nonlinear dynamics based regression model in the latent space to identify functionals corresponding to missing dynamics in the simulation model. We demonstrate that DA-SHRED successfully closes the SIM2REAL gap and additionally recovers missing dynamics in highly complex systems, demonstrating that the combination of efficient temporal encoding and physics-informed correction enables robust data assimilation.
Data-driven science and engineering is being revolutionized by advancements in machine learning and AI algorithms [1]. Leveraging sensor measurements, often in combination with scientific computation proxies, such algorithms aim to learn effective models for a diversity of downstream tasks, including reconstruction, forecasting, and control in challenging environments that include noisy measurements and or parametric variability. A grand challenge in the deployment of such algorithms is the fact that many physical systems are not amenable to full state measurements, but rather only discrete point sensor measurements at prescribed and limited locations. In fact, the only knowledge of the full state space is typically approximated by simulations of the underlying governing equations which are often given by partial differential equations (PDEs). For example, our knowledge of the full dynamics of nuclear reactors, plasma physics, rocket engines, and many complex flow fields has only been estimated and/or constructed by simulation proxies. Some nuclear reactors, for instance, are modeled by up to 20 coupled PDEs that detail the complex interactions between the fluid dynamics, thermodynamics, ion concentrations, etc [2]. None of the 20 fields have been measured in practice in deployed reactors. Rather, in reality only one or two of the fields (e.g. temperature, pressure) can be measured at discrete point sensor locations on the walls of the reactor. This presents a significant modeling challenge for closing the simulation-to-reality (SIM2REAL) gap [3,4], especially as the PDEs we simulate often poorly approximate the real physics of such complex systems. Using the recently developed SHallow REcurrent Decoder (SHRED) architecture [5,6,7], we demonstrate a data-driven method for (i) updating a SHRED model to reality when trained only on simulations and (ii) additionally learning the missing physics of the simulation proxy. Our data assimilation SHRED (DA-SHRED) thus provides an effective algorithm for closing the SIM2REAL gap in many complex systems, as demonstrated in the challenging examples presented here which include applications in rocket engines, chemical reactors and turbulent flows.
Data assimilation has become the leading method for closing the SIM2REAL gap across science and engineering [8], with extensive theoretical and computational developments over the past two decades [9,10]. Based upon Kalman filtering, data assimilation is potentially one of the most useful and broadly deployed data-driven modeling technique available today as we are rarely without access to some underlying governing equations or without experimental measurements. By assuming that both the model used and the measurements acquired have known error distributions, ensemble Kalman filtering methods [11,12] can be used to generate optimal statistical predictions. Weather forecasting has been revolutionized by data assimilation, with state-of-the-art methods like the 4DVAR architecture [13,14] providing a remarkable improvement in our modern forecasting capabilities. Data assimilation, however, does not typically use the SIM2REAL mismatch to learn updates to the underlying model. Thus the SIM2REAL gap often persists. Discrepancy modeling for dynamic systems [15,16,17] attempts to address this issue by using the SIM2REAL gap to propose updates to the underlying model in order to correct the physics towards reality. Discrepancy modeling is thus driven by sensor measurements which are a direct assessment of reality modulo noise or bias in the measurements. A challenge for both data assimilation and discrepancy modeling is that simulations allow access to all variables at all spatial and temporal points of a computational mesh or grid. In contrast, discrete temporal measurements of reality are typically only acquired at a limited number of spatial positions, and typically only a subset of the variables are actually observed. Thus the goal of updating the underlying PDE (governing equations) is exceptionally challenging, with only limited methods proposed thus far.
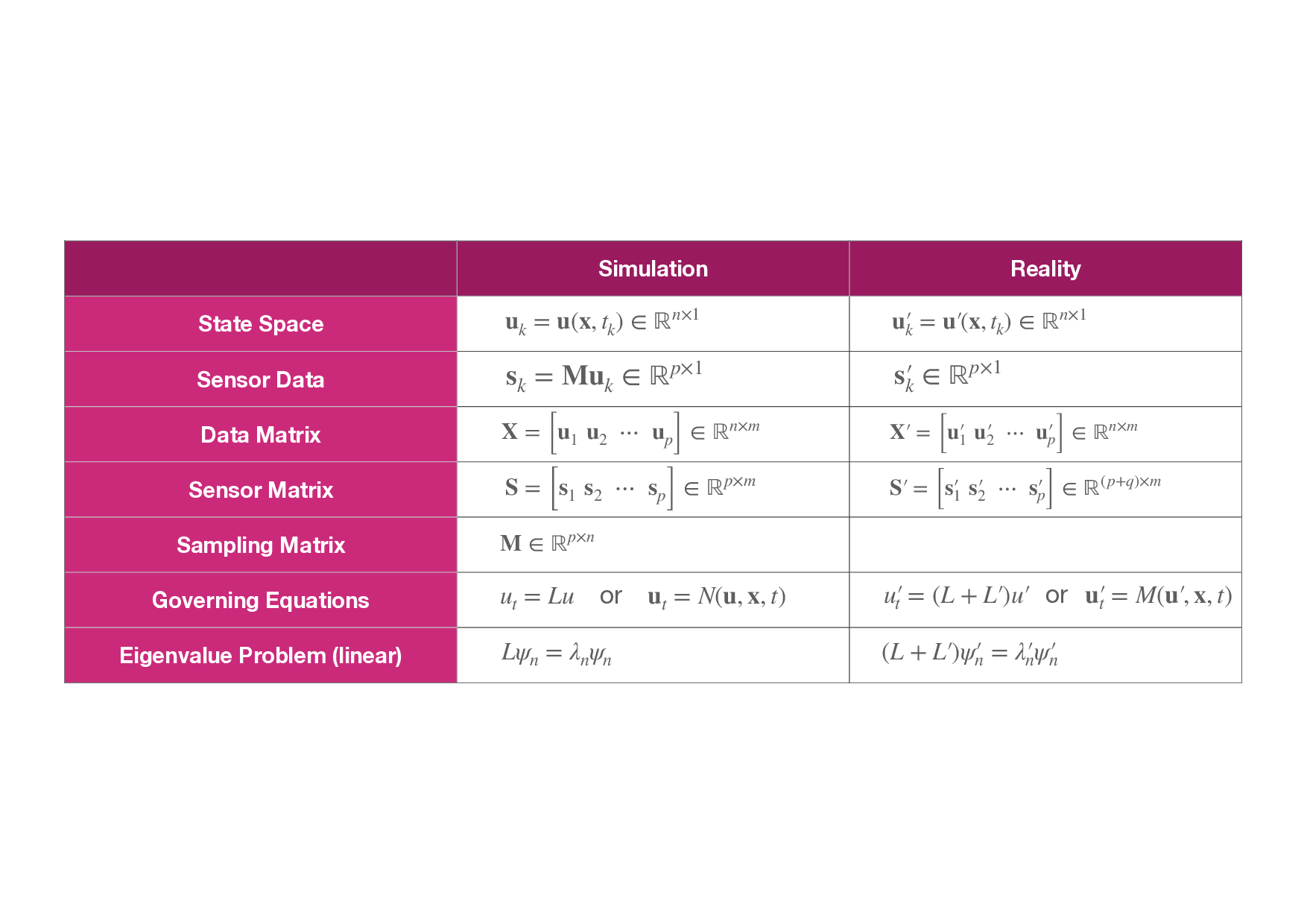
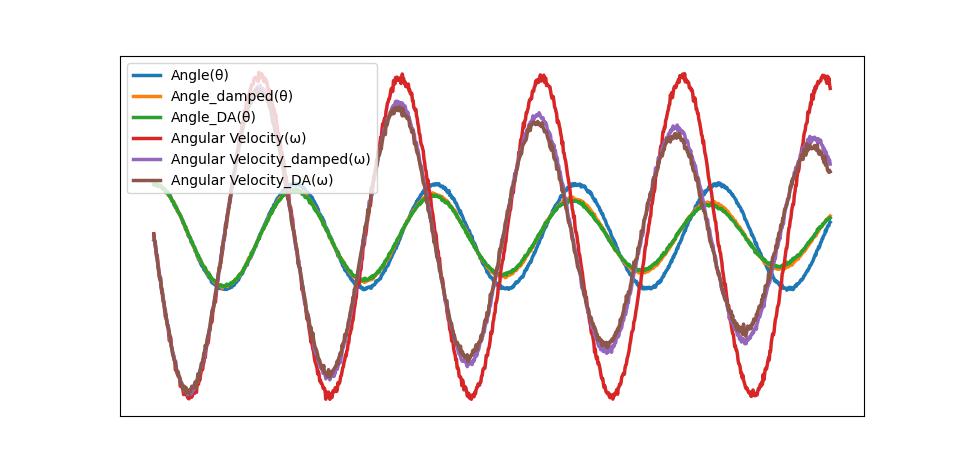
The DA-SHRED algorithm proposed here, illustrated in Fig. 1, is based upon the SHRED architecture [
M ∈ ℝ p×n u t = Lu or u t = N(u, x, t) u′ t = (L + L′ )u′ or u′ t = M(u′ , x, t)
Lψ n = λ n ψ n (L + L′ )ψ′ n = λ′ n ψ′ n Figure 2: Summary of variables, data and models used in the DA-SHRED formulation. The state space is of dimension n, there are m snapshots of temporal measurements using p sensors for SHRED training with an additional q sensors deployed in reality.
6, 7] which leverages three key mathematical concepts: (i) the separation of variables, (ii) Takens embedding theorem, and (iii) a decoding only strategy. Separation of variables is the foundation of many analytic solutions techniques for solving PDEs and it has been deployed as the infrastructure for numerical time stepping methods for PDEs. Takens’ embedding theorem states that the time-history information at
This content is AI-processed based on open access ArXiv data.