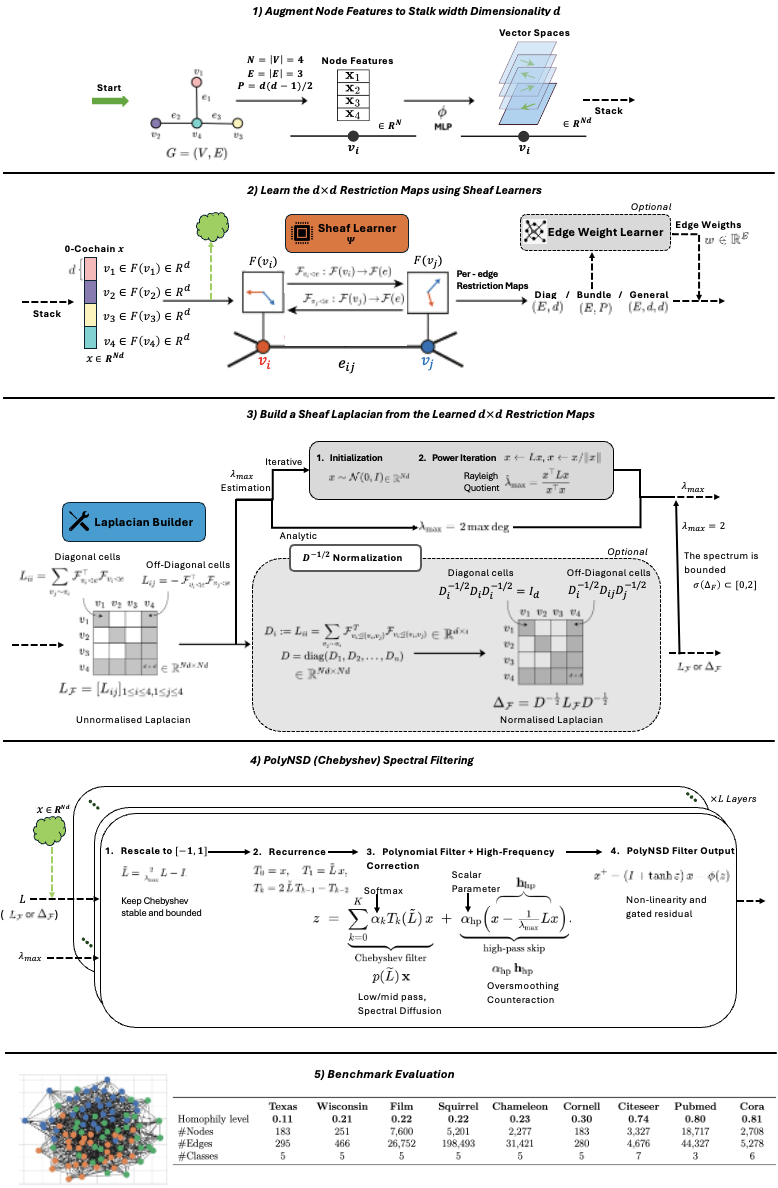
Sheaf Neural Networks equip graph structures with a cellular sheaf: a geometric structure which assigns local vector spaces (stalks) and a linear learnable restriction/transport maps to nodes and edges, yielding an edge-aware inductive bias that handles heterophily and limits oversmoothing. However, common Neural Sheaf Diffusion implementations rely on SVD-based sheaf normalization and dense per-edge restriction maps, which scale with stalk dimension, require frequent Laplacian rebuilds, and yield brittle gradients. To address these limitations, we introduce Polynomial Neural Sheaf Diffusion (PolyNSD), a new sheaf diffusion approach whose propagation operator is a degree-K polynomial in a normalised sheaf Laplacian, evaluated via a stable three-term recurrence on a spectrally rescaled operator. This provides an explicit K-hop receptive field in a single layer (independently of the stalk dimension), with a trainable spectral response obtained as a convex mixture of K+1 orthogonal polynomial basis responses. PolyNSD enforces stability via convex mixtures, spectral rescaling, and residual/gated paths, reaching new state-of-the-art results on both homophilic and heterophilic benchmarks, inverting the Neural Sheaf Diffusion trend by obtaining these results with just diagonal restriction maps, decoupling performance from large stalk dimension, while reducing runtime and memory requirements.
Graph Neural Networks (GNNs) Goller & Kuchler (1996); Gori et al. (2005); Scarselli et al. (2008); Bruna et al. (2013); Defferrard et al. (2016); Velickovic et al. (2017); Gilmer et al. (2017) have become a standard tool for learning on relational data, yet they often underperform on heterophilic graphs (Zhu et al., 2020) and suffer from oversmoothing (Nt & Maehara, 2019;Rusch et al., 2023) when stacked deeply.
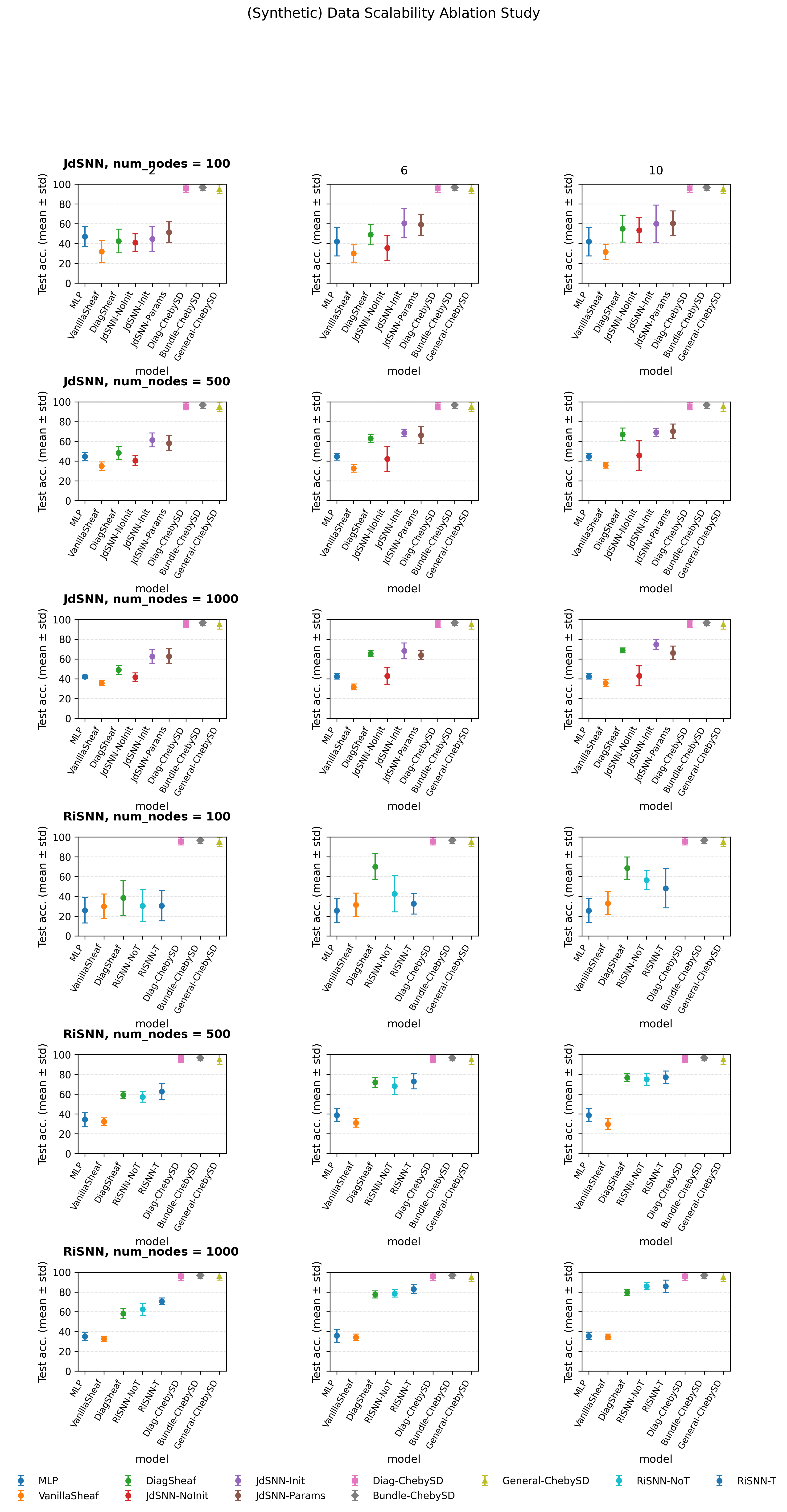
A possible solution provided by (Bi et al., 2024) is to modify the graph by rewiring the graph with homophilic edges and pruning heterophilic ones. A more principled way to avoid that, modeling heterophily in the graph’s underlying topology, is via (cellular) sheaves (Hansen & Gebhart, 2020;Bodnar et al., 2022): each node/edge carries a local feature space (a stalk) and edges carry linear restriction maps that specify how to align and compare features across incidences. The resulting sheaf Laplacian implements transport-aware diffusion that can better accommodate heterophily than conventional, isotropic graph filters. However, existing neural sheaf-diffusion layers are (i) effectively one-step propagators, (ii) rely on dense, per-edge restriction maps, (iii) require heavy normalizations or even decompositions during training, and (iv) their performance is highly dependent on the stalk’s high-dimensionality. These factors inflate parameters and runtime, couple cost and stability to the stalk dimension, and can yield brittle optimization.
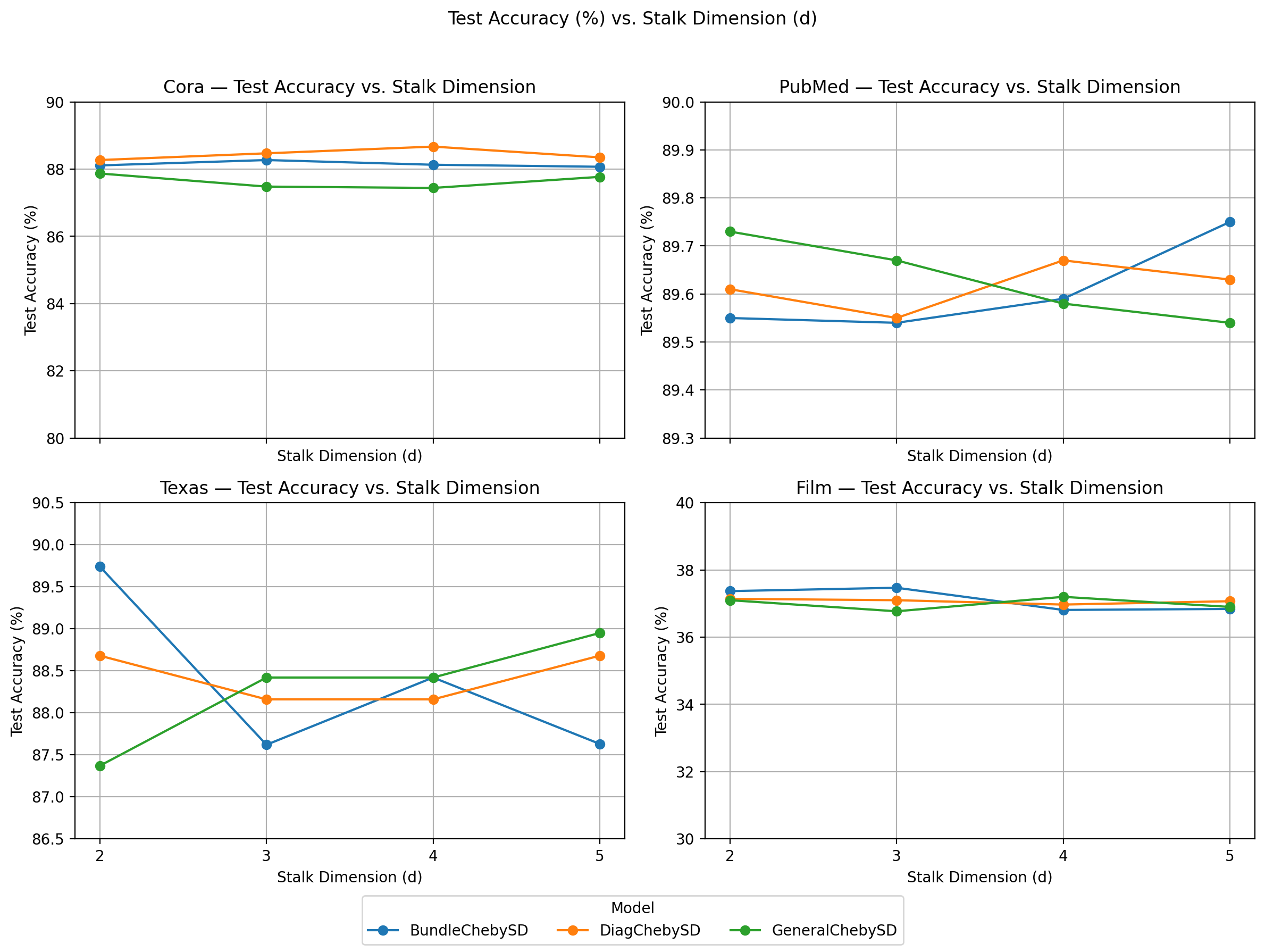
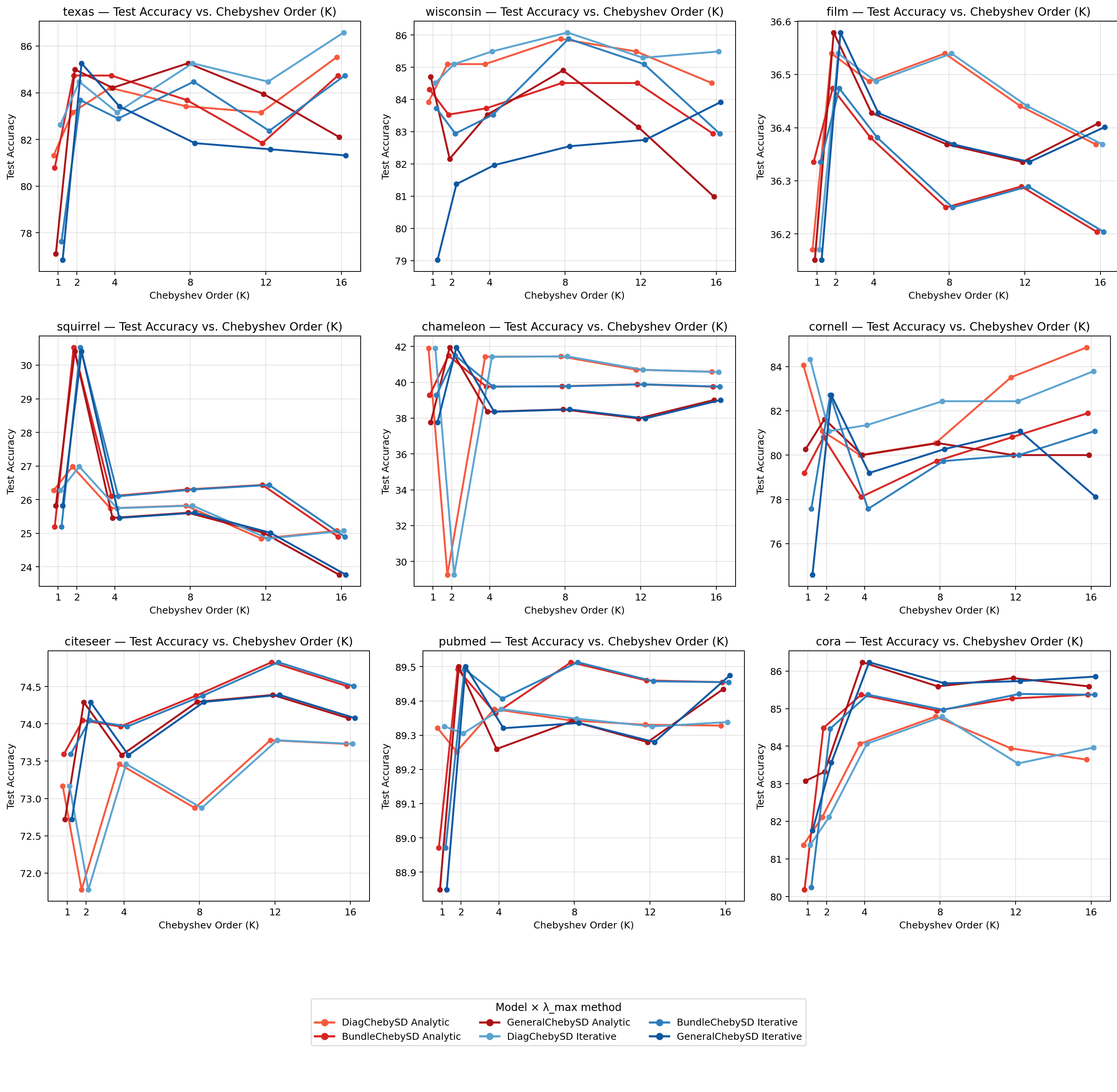
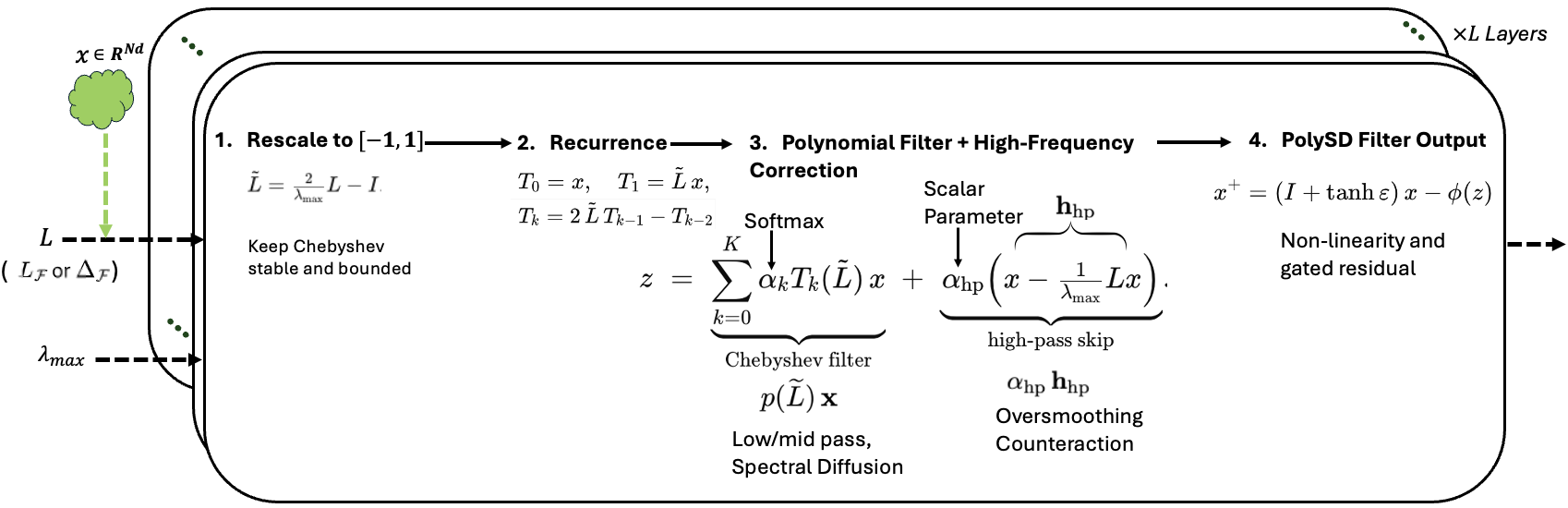
We propose Polynomial Neural Sheaf Diffusion (PolyNSD), which reframes neural sheaf diffusion as an explicit spectral filtering problem. Instead of single-step spatial updates, PolyNSD applies a learnable degree-K polynomial filter of a spectrally rescaled sheaf Laplacian, evaluated via stable K-term recurrences (e.g., Chebyshev). This construction provides an explicit K-hop receptive field within a single layer and enables direct control over the diffusion behaviour (low-, band-, or high-pass). We ensure stability through spectral rescaling and convex combinations of the K+1 polynomial basis responses, yielding a non-expansive propagation operator, while residual and gated pathways preserve gradient flow at depth. PolyNSD is also parameter-efficient: propagation is governed by only K+1 scalar coefficients per layer, and reusing the learned sheaf transports, avoids dense per-edge restriction maps. For these reasons, with PolyNSD,
Sheaf Neural Networks, Heterophily and Oversmoothing. GNNs have evolved from early message-passing formulations to a family of architectures that trade off locality, expressivity, and efficiency. Canonical baselines include spectral and spatial convolutions (Defferrard et al., 2016;Bruna et al., 2013;Kipf & Welling, 2016), attention mechanisms (Velickovic et al., 2017), principled aggregates (Gilmer et al., 2020) and transformer-based versions (Yun et al., 2019;Dwivedi & Bresson, 2020). Despite this progress, two persistent pathologies limit standard GNNs. The former, Oversmoothing arises as layers deepen, since repeated low-pass propagation collapses node features toward a near-constant signal, eroding class margins and yielding accuracy drop-offs beyond shallow depth (Nt & Maehara, 2019;Rusch et al., 2023). Heterophily further stresses isotropic message passing: when adjacent nodes belong to different classes or carry contrasting attributes, the averaging operation blurs the high-frequency signals that separate classes, and performance degrades as homophily decreases (Zhu et al., 2020). These phenomena are tightly linked in practice and motivate transport-aware architectures that decouple who communicates from how features are compared.
Sheaf Neural Networks. Cellular sheaf theory (Shepard, 1985;Curry, 2014) equips graphs with local feature spaces (stalks) and linear restriction/transport maps on edges, enabling transport-aware diffusion that can better handle heterophily than isotropic message passing. Sheaf Neural Networks, originally introduced using an hand-crafted sheaf with a single dimensionality in (Hansen & Gebhart, 2020) and further improved by allowing to learn the sheaf using a learnable parametric function (Bodnar et al., 2022), demonstrated strong performance under heterophily and against oversmoothing, by instantiating diffusion on the sheaf Laplacian. Subsequent works explored attention on sheaves (Barbero et al., 2022b), learning the graph connection Laplacian directly from data and at preprocessing time (Barbero et al., 2022a), sheaves-based positional encoding (He et al., 2023), introducing non-linearities in the process (Zaghen, 2024), injecting joint diffusion biases (Caralt et al., 2024), handling graph heterogeneity (Braithwaite et al., 2024), sheaf hypergraphs (Duta et al., 2023;Mule et al., 2025) and directional extensions (Fiorini et al., 2025), applications to recommendation systems (Purificato et al., 2023) and federated learning settings (Nguyen et al., 2024), and more general frameworks such as Copresheafs
This content is AI-processed based on open access ArXiv data.