Recent studies on Neural Collapse (NC) reveal that, under class-balanced conditions, the class feature means and classifier weights spontaneously align into a simplex equiangular tight frame (ETF). In long-tailed regimes, however, severe sample imbalance tends to prevent the emergence of the NC phenomenon, resulting in poor generalization performance. Current efforts predominantly seek to recover the ETF geometry by imposing constraints on features or classifier weights, yet overlook a critical problem: There is a pronounced misalignment between the feature and the classifier weight spaces. In this paper, we theoretically quantify the harm of such misalignment through an optimal error exponent analysis. Built on this insight, we propose three explicit alignment strategies that plug-and-play into existing long-tail methods without architectural change. Extensive experiments on the CIFAR-10-LT, CIFAR-100-LT, and ImageNet-LT datasets consistently boost examined baselines and achieve the state-of-the-art performances.
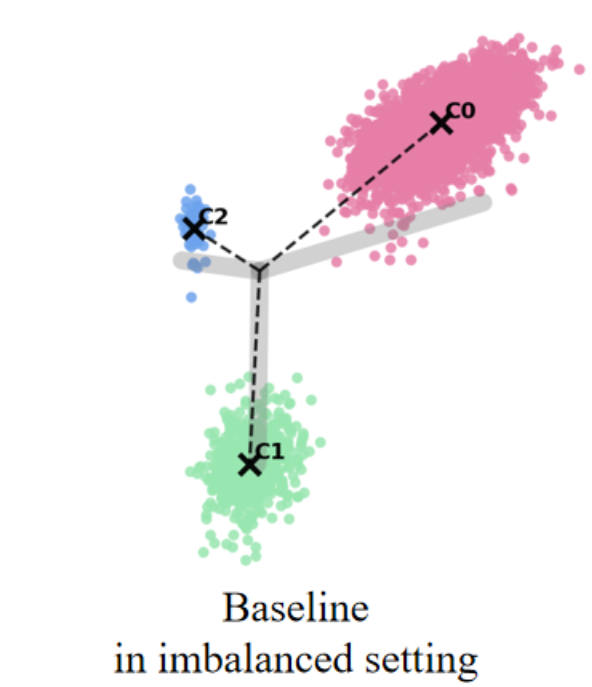
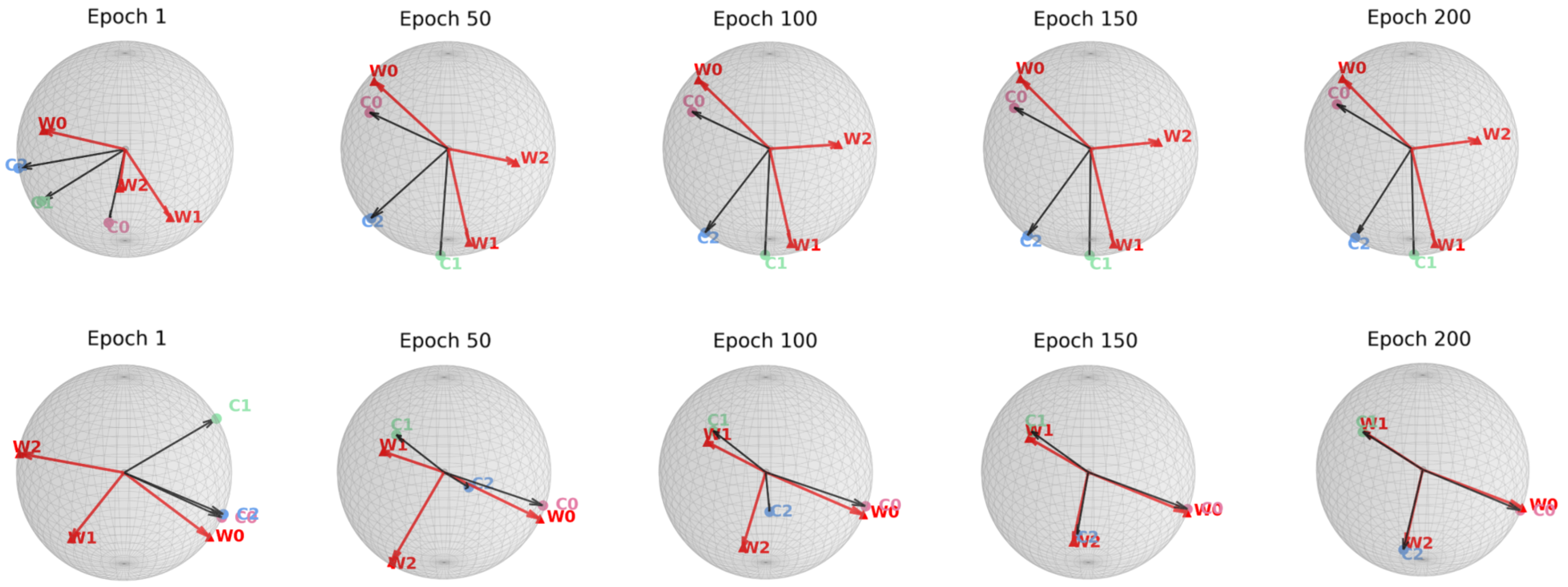
Long-tailed learning refers to scenarios where a few head classes dominate the dataset, while numerous tail classes have scarce examples. This distribution poses a significant challenge for neural networks, often resulting in suboptimal feature learning, biased predictions toward head classes, and poor generalization on minority classes (Fang et al. 2021). In contrast, when trained on balanced data, as shown in However, under long-tail distributions, the NC structure is disrupted, leading to a common failure mode termed Minority Collapse, where classifier weights for tail classes degenerate to nearly identical directions, inducing severe misclassification. As highlighted by (Yang et al. 2022), this is due to the imbalance in gradient contributions: majority classes dominate both attraction (intra-class compactness) and repulsion (inter-class separation) terms, while minority classes contribute negligibly. Consequently, classifier weights of tail arXiv:2512.07844v1 [cs.LG] 25 Nov 2025 classes are overwhelmed by repulsion from head classes, and their updates deviate from the NC geometry. The resulting biased decision boundaries favor majority classes and suppress minority accuracy.
To mitigate this, recent studies have attempted to reconstruct the ETF structure (NC1 and NC2), either by manually producing classifier weights (Yang et al. 2022), class prototypes (Zhu et al. 2022), handcrafted ETF structure (Gao et al. 2024), or reshaping the feature space into a more stable configuration (Peifeng et al. 2023;Xie et al. 2023;Liu et al. 2023). However, these approaches overlook an important question: To what extent existing methods achieve feature-classifier alignment (NC3), and whether explicitly promoting this alignment is beneficial? Intuitively, enforcing this alignment is helpful for further inducing NC in long-tail learning, which will encourage a better representation learning and provide a extra performance improvement.
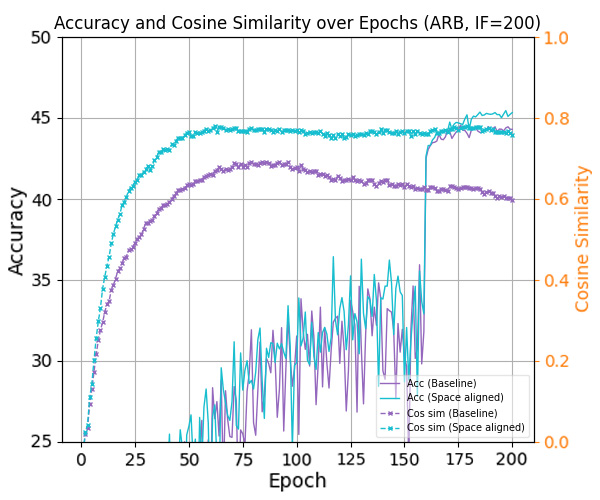
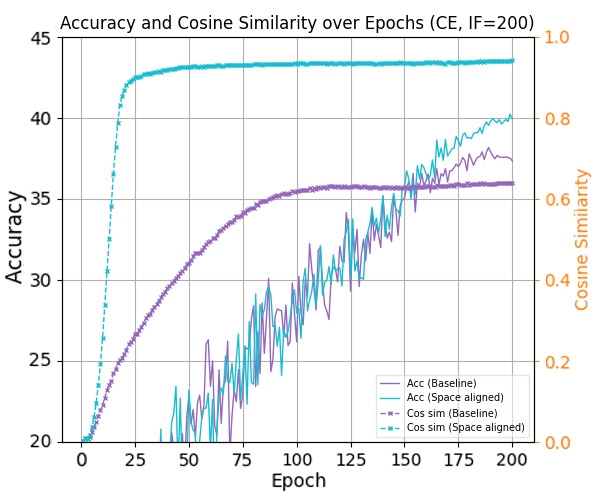
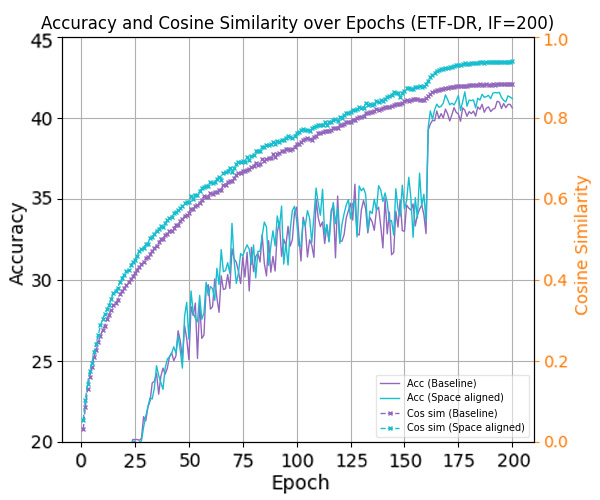
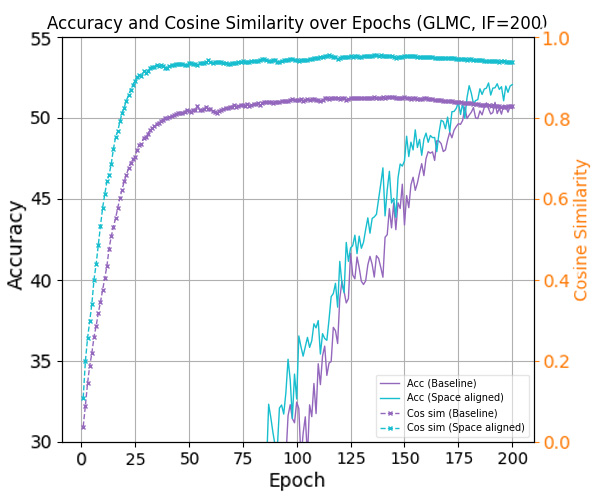
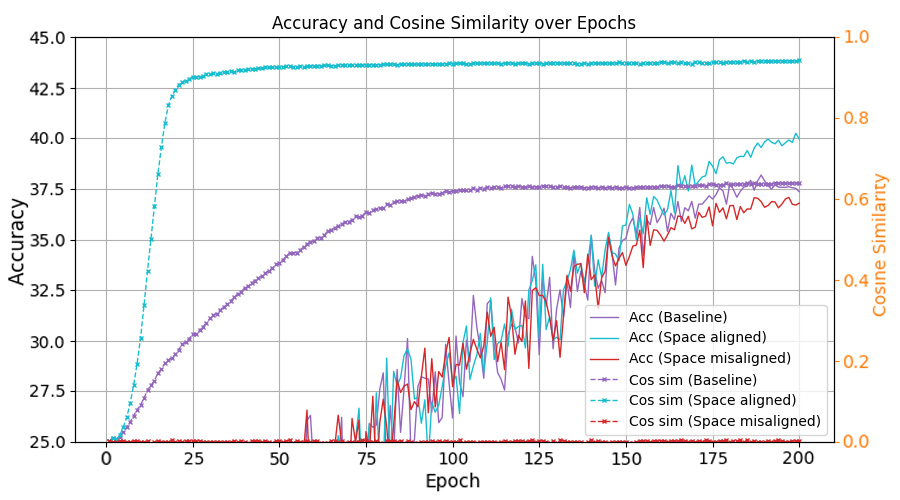
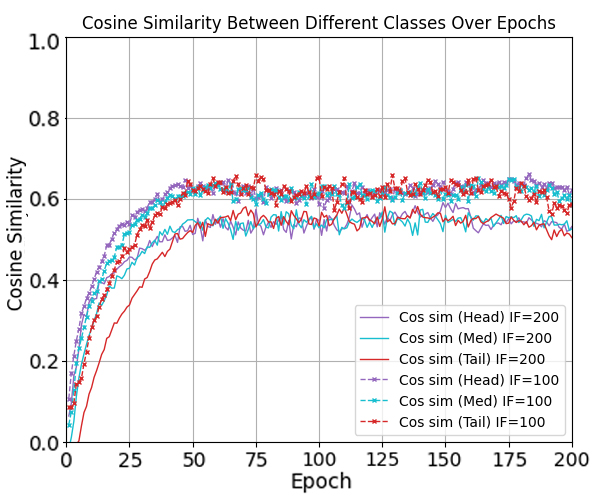
To answer this, we study the space misalignment between feature and classifier vectors in long-tailed settings. As visualized in Figure 1(c), models trained with cross-entropy loss fail to achieve alignment, in contrast to the balanced case in Figure 1(b). We further observe that the similarity between these spaces correlates strongly with performance: Compared to baseline (purple curve), applying a constraint that further reduces this alignment (red curve) leads to consistent performance degradation. This suggests that space misalignment is not merely a by-product, but a core obstacle to robust representation learning under imbalance.
To formally analyze this, we introduce a geometric framework based on the Optimal Error Exponent (OEE) which is a classical information-theoretic measure that quantifies how quickly misclassification probability decays as the noise level decreases. We show that angular misalignment between feature and classifier directions provably slows convergence and deteriorates generalization. This analysis provides theoretical insight suggesting that even moderate misalignment can significantly deteriorate the generalization performance of the model. Motivated by this, we propose three plug-and-play strategies to reduce space misalignment in standard long-tailed learning setups. As shown in Figure 1(d), our regularization leads to high alignment, and consistently improves both space similarity and classification accuracy (blue line in Figure 1(a)). Through extensive experiments on benchmarks, our approach achieves state-ofthe-art performance while recovering stronger NC properties in both feature and decision spaces.
The training set consists of C classes, where the given dataset is balanced; each class contains n samples and can be denoted as {(x i,c , y i,c )}. Here, x i,c ∈ R d denotes the i th input sample of class c and y i,c = c denotes its real label. The model is composed of a deep neural network. We can consider the layers before the classifier, which act as a feature extractor as a mapping h: R d → R p that outputs a p-dimensional feature vector h(x). Following this, a linear classifier with weight matrix W ∈ R C×p and biases b ∈ R C takes the last-layer features as inputs and then outputs the class label. In detail, through classification scores via f (x) = Wh(x) + b, the predicted label is then given by argmax c ′ ⟨w c ′ , h⟩ + b c ′ , where w c ′ denotes the classifier weight for a specific class. Furthermore, we denote the class mean µ c = 1 n n i=1 h(x i,c ) and the global mean
A general Simplex Equiangular Tight Frame (Simplex ETF) matrix M ∈ R p×C is a collection of points in R C specified by the columns of:
where I ∈ R C×C is the identity matrix and 1 C ∈ R C×1 is the ones vector, and
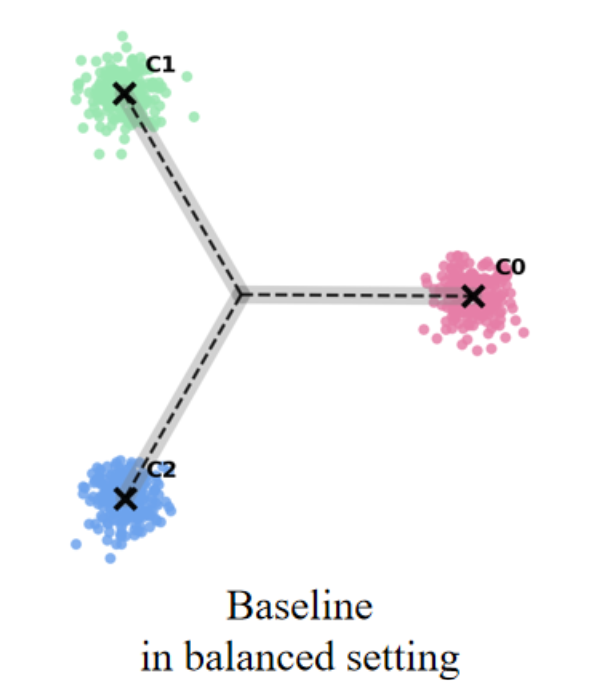
In the terminal phase of training on balanced datasets, as shown in Figure 1(b), it can be observed that the last-layer features will converge to class means, which in turn align with classifier weights, all forming the vertices of a symmetric simplex ETF (Papyan,
This content is AI-processed based on open access ArXiv data.