If a line cuts randomly two sides of a triangle, the length of the segment determined by the points of intersection is also random. The object of this study, applied to a particular case, is to calculate the probability that the length of such segment is greater than a certain value.
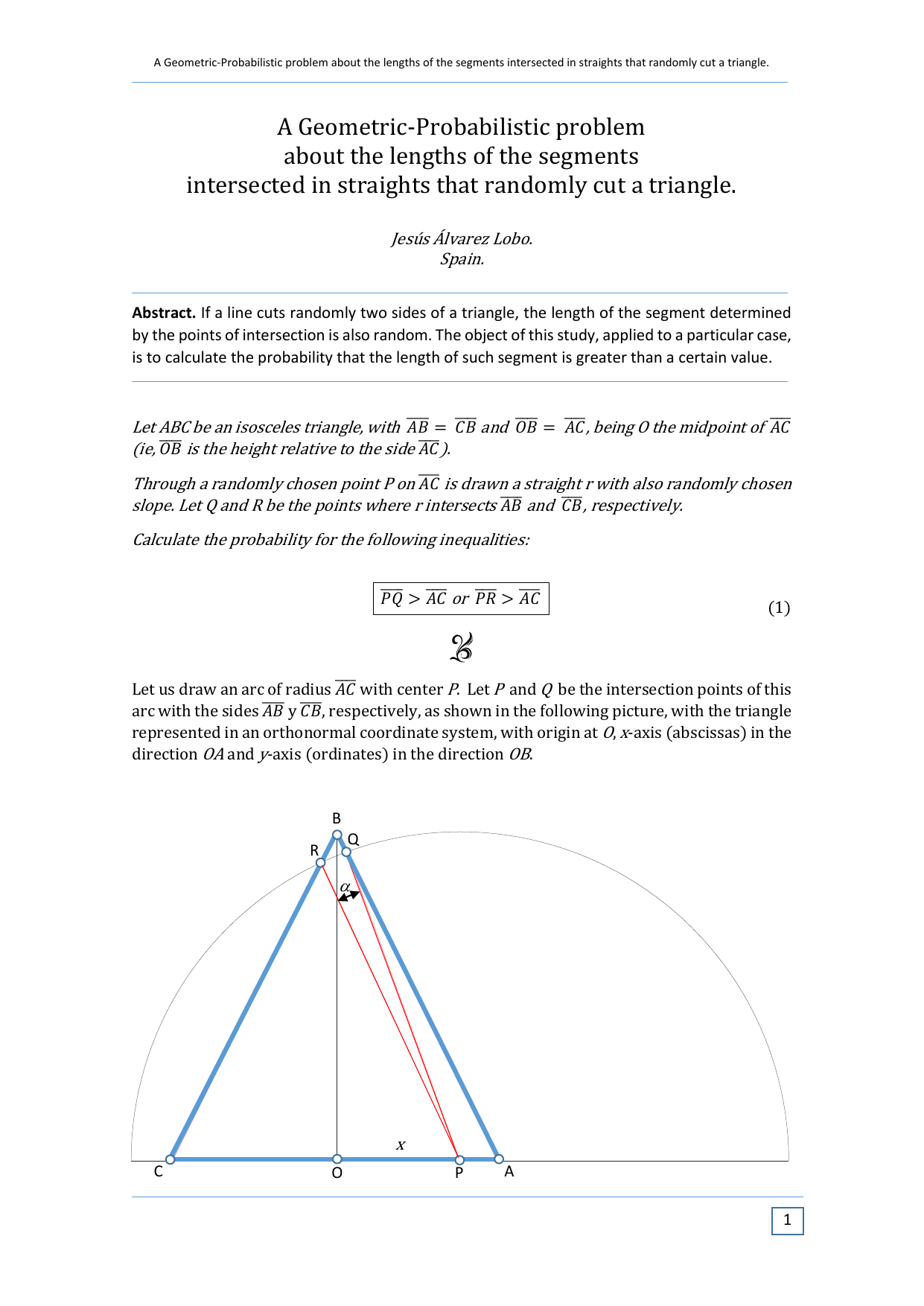
Let ABC be an isosceles triangle, with 𝐴𝐵 ̅̅̅̅ = 𝐶𝐵 ̅̅̅̅ and 𝑂𝐵 ̅̅̅̅ = 𝐴𝐶 ̅̅̅̅ , being O the midpoint of 𝐴𝐶 ̅̅̅̅ (ie, 𝑂𝐵 ̅̅̅̅ is the height relative to the side 𝐴𝐶 ̅̅̅̅ ).
Through a randomly chosen point P on 𝐴𝐶 ̅̅̅̅ is drawn a straight r with also randomly chosen slope. Let Q and R be the points where r intersects 𝐴𝐵 ̅̅̅̅ and 𝐶𝐵 ̅̅̅̅ , respectively.
Calculate the probability for the following inequalities: (1) x Let us draw an arc of radius 𝐴𝐶 ̅̅̅̅ with center P. Let P and Q be the intersection points of this arc with the sides 𝐴𝐵 ̅̅̅̅ y 𝐶𝐵 ̅̅̅̅ , respectively, as shown in the following picture, with the triangle represented in an orthonormal coordinate system, with origin at O, x-axis (abscissas) in the direction OA and y-axis (ordinates) in the direction OB.
Clearly, all the straight lines of the bundle with vertex P in 𝐴𝐶 ̅̅̅̅ intersect the sides 𝐴𝐵 ̅̅̅̅ or 𝐶𝐵 ̅̅̅̅ , and all the lines of the sub-bundle inner to the angle 𝛼 = 𝑄𝑃𝑅 ̂, and only them, satisfies (1). Since x and are continuous random variables uniformly distributed, for a differential of length dx in 𝐴𝐶 ̅̅̅̅ , the probability that the condition (1) is satisfied will be (2) and therefore, the probability that the inequalities (1) are satisfied for a randomly chosen point in 𝐴𝐶 ̅̅̅̅ will be (3) where 𝛼(𝑥) is the function relating the angle with the abscissa x.
We have used the following facts:
In an infinitesimal length, dx, the limit angle is constant. The slope of the secant line is independent of the abscissa x.
The required probability p is obtained by Riemann integration of the probability density function 𝛼(𝑥) in the symmetric interval 𝐴𝐶 ̅̅̅̅ = [-1 2 , 1 2 ].
The limit angle can be expressed in radians as:
(4) But,
(5)
Perhaps the easiest way to define 𝛼 as a function of x is trigonometrically: :
:
And applying the formula of integration by parts,
After simplifying the sub-integral expression, through the elementary transformations shown below, 𝐼 3 is reduced to two quasi-immediate integrals (reducible to immediate integrals by simple adjustment of constants). Omitting integration constants, for simplicity:
From ( 18) and ( 19), ; substituting in this the result given by ( 20),
From ( 16), , and substituting therein the result given by ( 21),
And by a procedure completely analogously, we obtain ( 23)
Substituting in (13) this results, we obtain the exact value of the requested probability:
(24)
The expression (24) can be simplified considering the definition of the golden ratio [1] and the following identity regarding tangent arcs (by the general shape established in [2] for the decomposition of pi / 4 in two arctan):
(25) This identity can be proven easily by the formula of the tangent of a sum or through algebra of complex numbers, expressing the product of two complex numbers (suitably chosen) in two representation forms, binary form and polar form, as shown below.
Product in binary form and its corresponding representation in polar form: After performed the product in polar form, the identity (25) is derived by identifying the arguments on both sides of the last equality:
(26) Finally, the result (24) can be expressed in the following elegant form that involves two of the most remarkable numbers: the number Pi and the Golden Ratio ,
As the number , it is surprising the ubiquity of this number, that emerge in the most diverse sceneries [1].
(28)
The approximate value of p in ten thousandths is, p 0.0162.
This content is AI-processed based on open access ArXiv data.