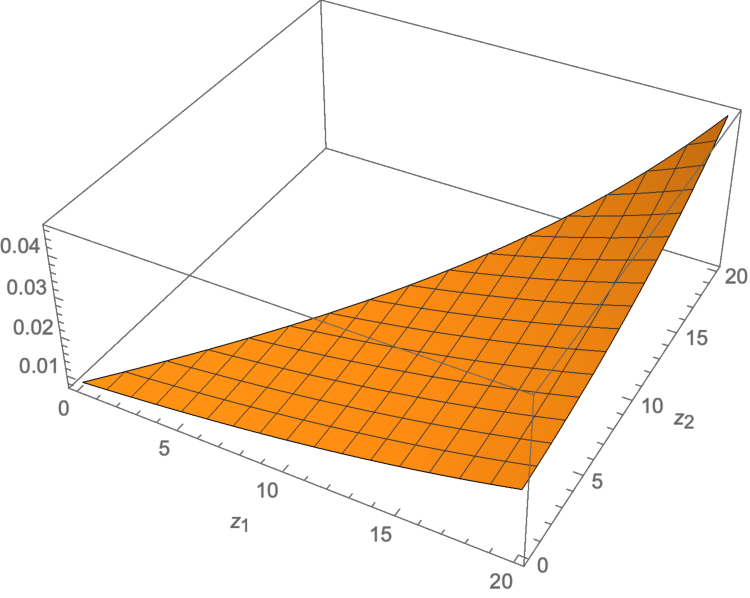
양자역학과 η 거의 허미트 연산자를 활용한 블랙 쇼울스 방정식 연구 2. 초록 전체 번역 및 정리
: 이 논문은 블랙 쇼울스(BS) 방정식을 양자역학적 관점에서 재해석하고, 이를 통해 금융 모델링에 새로운 접근법을 제시합니다. 특히, BS 함수와 그 일반화된 형태가 η 거의 허미트 연산자로 표현될 수 있음을 증명함으로써, 양자역학적 개념이 금융 분야에서 어떻게 활용될 수 있는지 탐구하고 있습니다. 논문은 먼저 BS 방정식을 슈뢰딩거 유사 방정식으로 변환하는 방법을 설명합니다. 이 과정에서 BS 함수 HBS가 비허미트임을 강조하며, 이를 η 거의 허미트 연산자로 표현할 수 있음을 보여줍니다. 이러한 접근법은 BS 방정식의 해석과