트리폭을 보존한 3‑다양체 삼각분할의 변환과 퀀텀 불변량의 고정‑파라미터 알고리즘
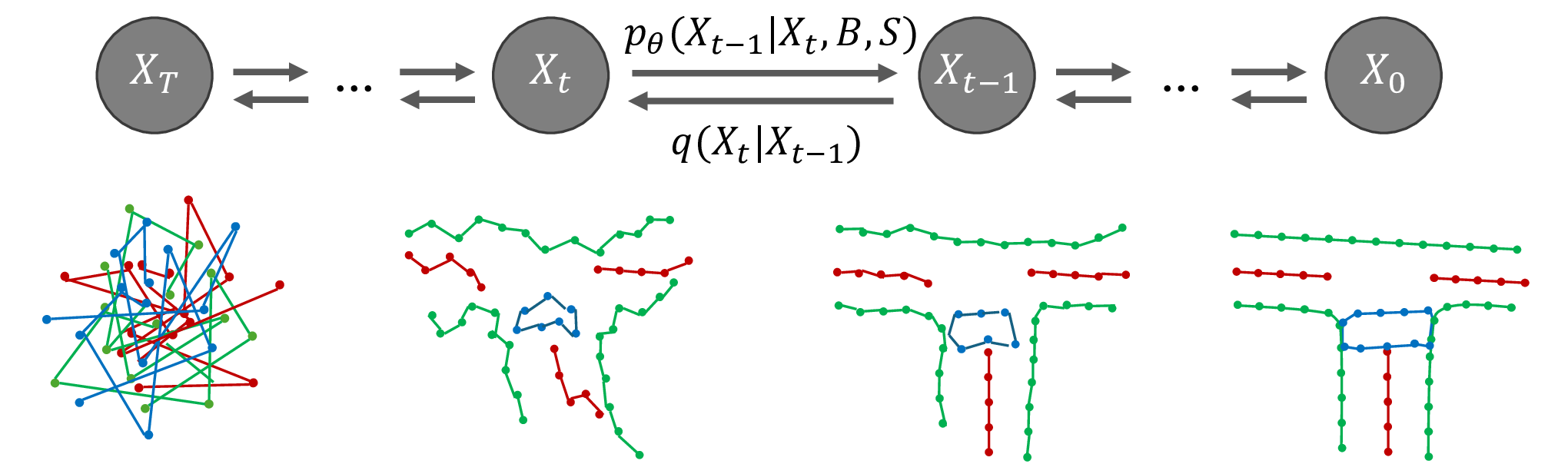
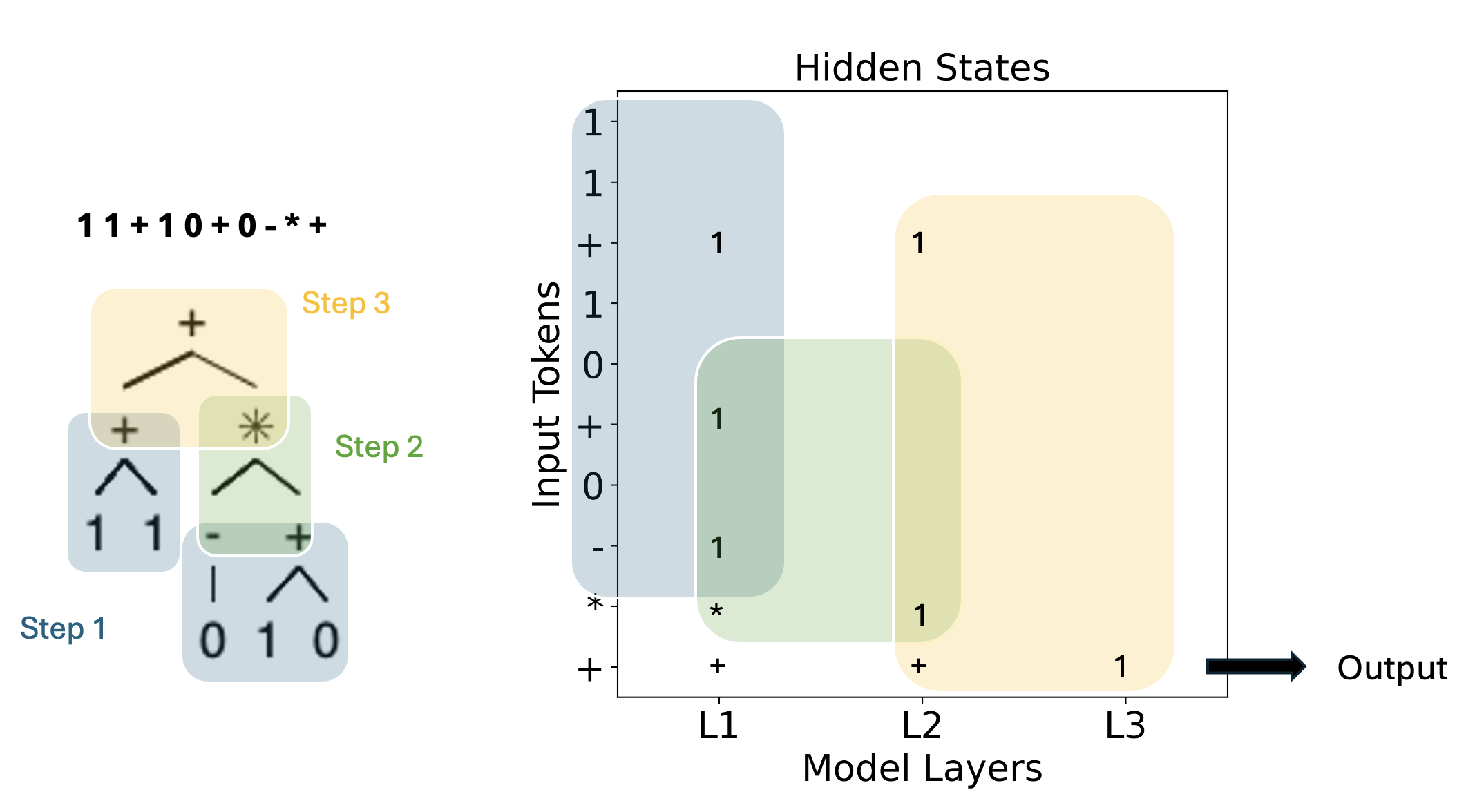
이 논문은 3‑다양체 위상학에서 가장 실용적인 데이터 구조인 삼각분할을 다루면서, 그래프 이론의 핵심 개념인 트리폭을 중심으로 알고리즘적 효율성을 극대화한다는 점에서 큰 의미를 가진다. 트리폭은 그래프가 트리와 얼마나 유사한지를 정량화하는 파라미터이며, 트리폭이 작을수록 동적 계획법이나 색칠 알고리즘 같은 전통적인 FPT 기법을 적용하기 용이하다. 기존 연구에서는 삼각분할 자체의 트리폭을 이용해 다양한 위상학적 문제(예: 매니폴드 동형판별, 코흐라 복합체 계산 등)를 FPT로 해결했지만, 히어로드 분할이라는 전혀 다른 표현으로 변환