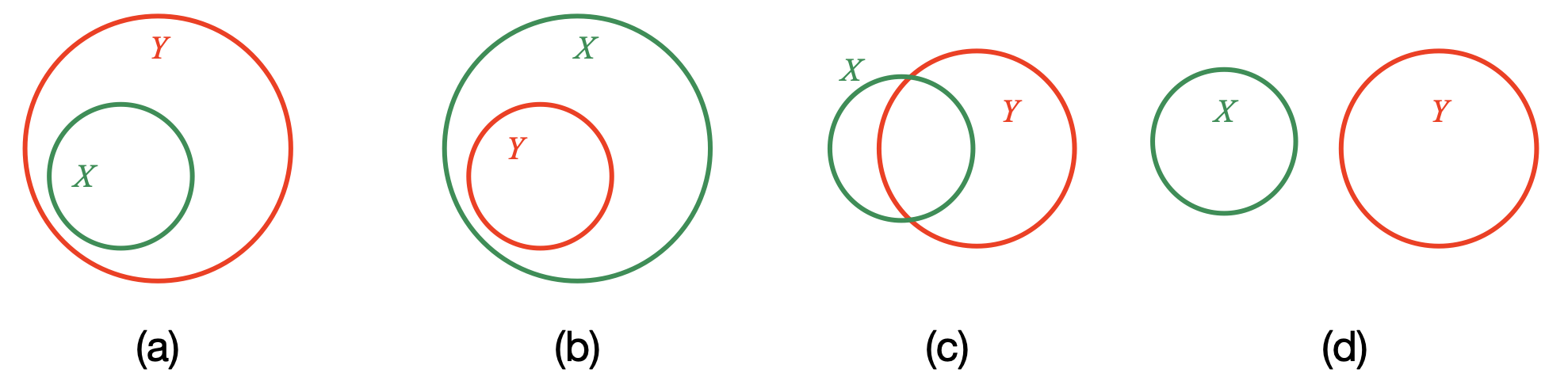Computer Science / Artificial Intelligence

구체 위에 원을 그리는 신경망, 확실히 포도 따기

2026년 01월 01일

읽는 시간: 5 분

...

#Network #Computer Science #Artificial Intelligence

📝 원문 정보

Title: An AI Monkey Gets Grapes for Sure – Sphere Neural Networks for Reliable Decision-Making
ArXiv ID: 2601.00142
발행일: 2026-01-01
저자: Tiansi Dong, Henry He, Pietro Liò, Mateja Jamnik

📝 초록 (Abstract)

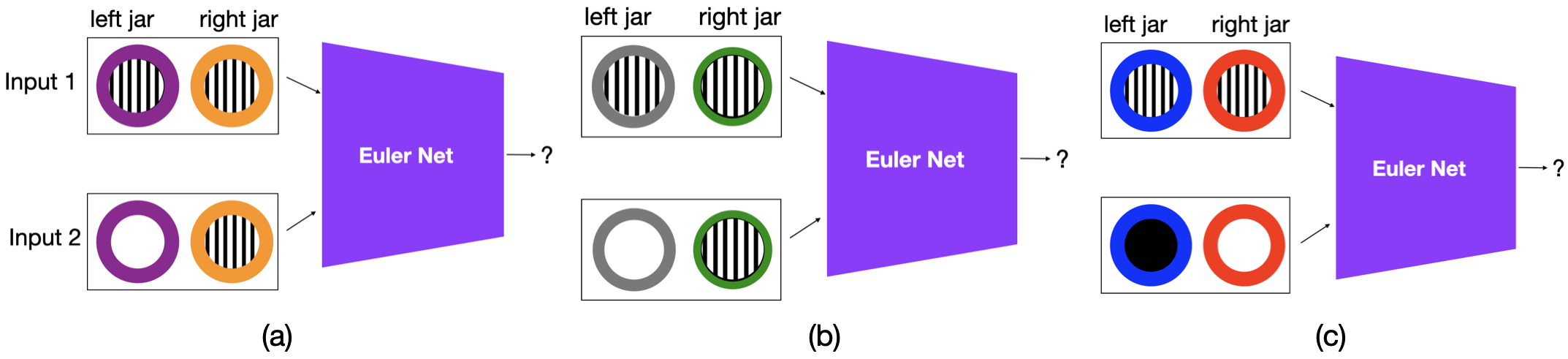
이 논문은 신경망 기반 추론 방법을 LLM 추론, 감독 학습 기반 추론, 그리고 명시적 모델 기반 추론의 세 가지 범주로 비교한다. 대규모 언어 모델(LLM)은 신뢰성이 낮으며, 동물이 별다른 대량 코퍼스 학습 없이도 마스터할 수 있는 단순 의사결정에서도 어려움을 보인다. 우리는 이분법적 삼단 논법 테스트를 통해 감독 학습에 의한 추론이 명시적 모델 구축에 의한 추론보다 매력적이지 않음을 입증한다. 구체적으로, 고전 삼단 논법에서 100 % 정확도를 달성하도록 훈련된 Euler Net을 이분법적 삼단 논법에서도 100 % 정확도로 재훈련할 수 있음을 보인다. 그러나 재훈련된 Euler Net은 심각한 재앙적 망각을 겪으며, 기존에 학습한 고전 삼단 논법 성능이 6.25 %로 급락하고, 추론 능력이 패턴 수준에 국한된다. 우리는 개념을 n차원 구 표면 위의 원으로 임베딩하는 새로운 Sphere Neural Networks 버전을 제안한다. 이 Sphere Neural Networks는 보완 원을 이용해 부정 연산자를 표현하고, 만족 불가능한 원형 구성을 형성하는 비논리적 진술을 필터링함으로써 신뢰할 수 있는 의사결정을 가능하게 한다. 실험 결과, Sphere Neural Network는 고전 삼단 논법의 엄격함을 유지하면서 16개의 삼단 논법 과제, 특히 이분법적 삼단 논법을 모두 마스터한다. 결론적으로, 명시적 모델 구축을 통한 신경망 추론이 세 가지 방법론 중 가장 신뢰할 수 있음을 주장한다.

💡 논문 핵심 해설 (Deep Analysis)

본 연구는 현재 인공지능 추론 분야에서 가장 논쟁이 되는 세 가지 접근법을 체계적으로 비교함으로써, “신뢰성”이라는 관점에서 중요한 통찰을 제공한다. 첫 번째 범주인 대규모 언어 모델(LLM) 기반 추론은 방대한 텍스트 코퍼스를 사전 학습함으로써 언어적 유연성을 얻지만, 논리적 일관성 유지와 같은 엄격한 판단에서는 여전히 불안정한 결과를 보인다. 이는 LLM이 통계적 패턴에 기반한 예측을 수행하기 때문에, 명시적인 논리 규칙을 내재화하지 못한다는 근본적인 한계와 연결된다. 두 번째인 감독 학습 기반 추론은 특정 논리 과제에 대해 라벨링된 데이터를 이용해 모델을 학습시키지만, 데이터가 충분히 다양하지 않으면 과적합 위험이 크고, 새로운 논리 형태(예: 이분법적 삼단 논법)로 전이할 때 재학습이 필요하다. 논문에서 제시된 Euler Net 사례는 재훈련 후 기존 과제에서 성능이 급격히 저하되는 재앙적 망각(catastrophic forgetting) 현상을 명확히 보여준다. 이는 파라미터 공유 방식이 논리 구조를 별도로 보존하지 못한다는 점을 시사한다.

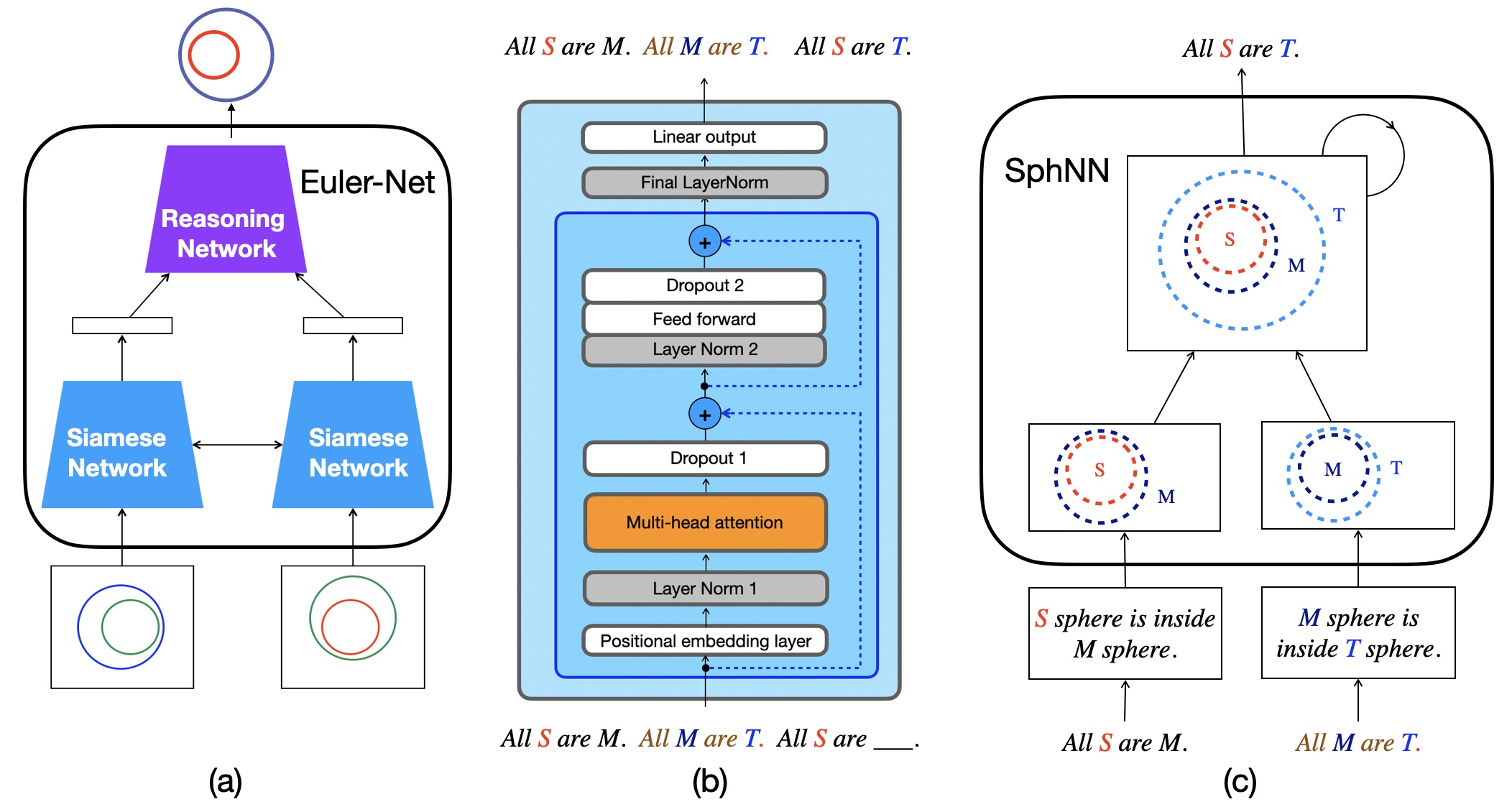
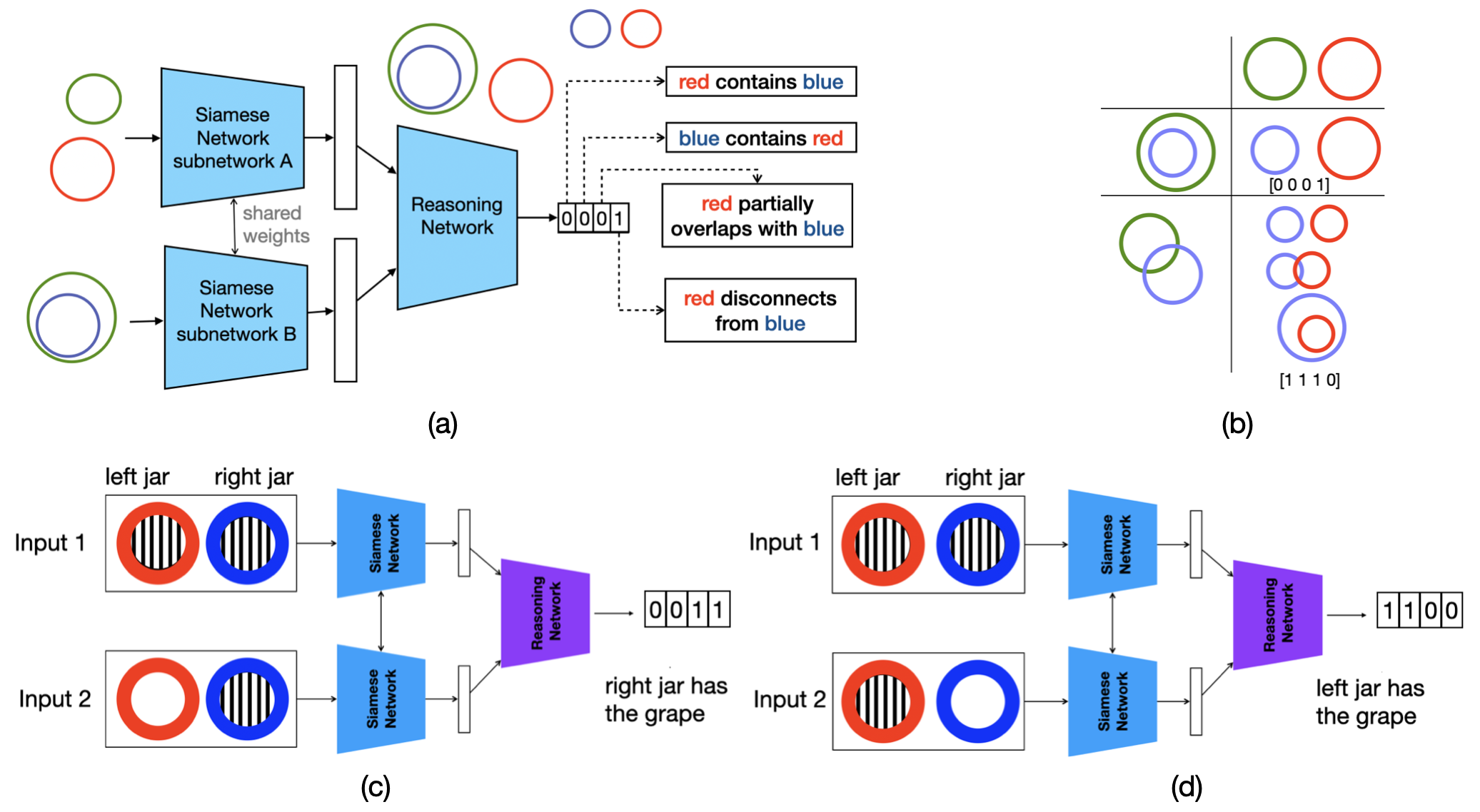
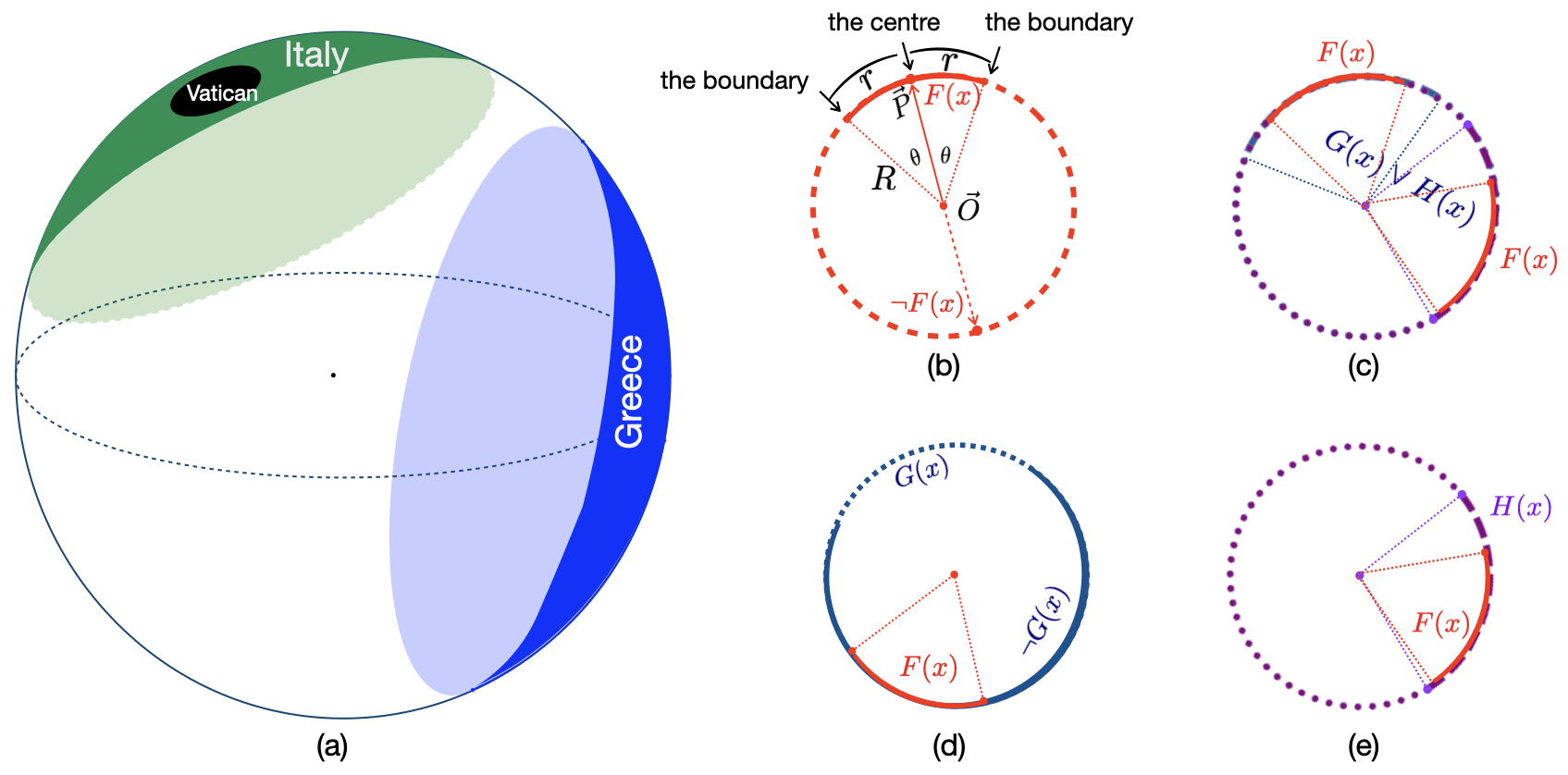
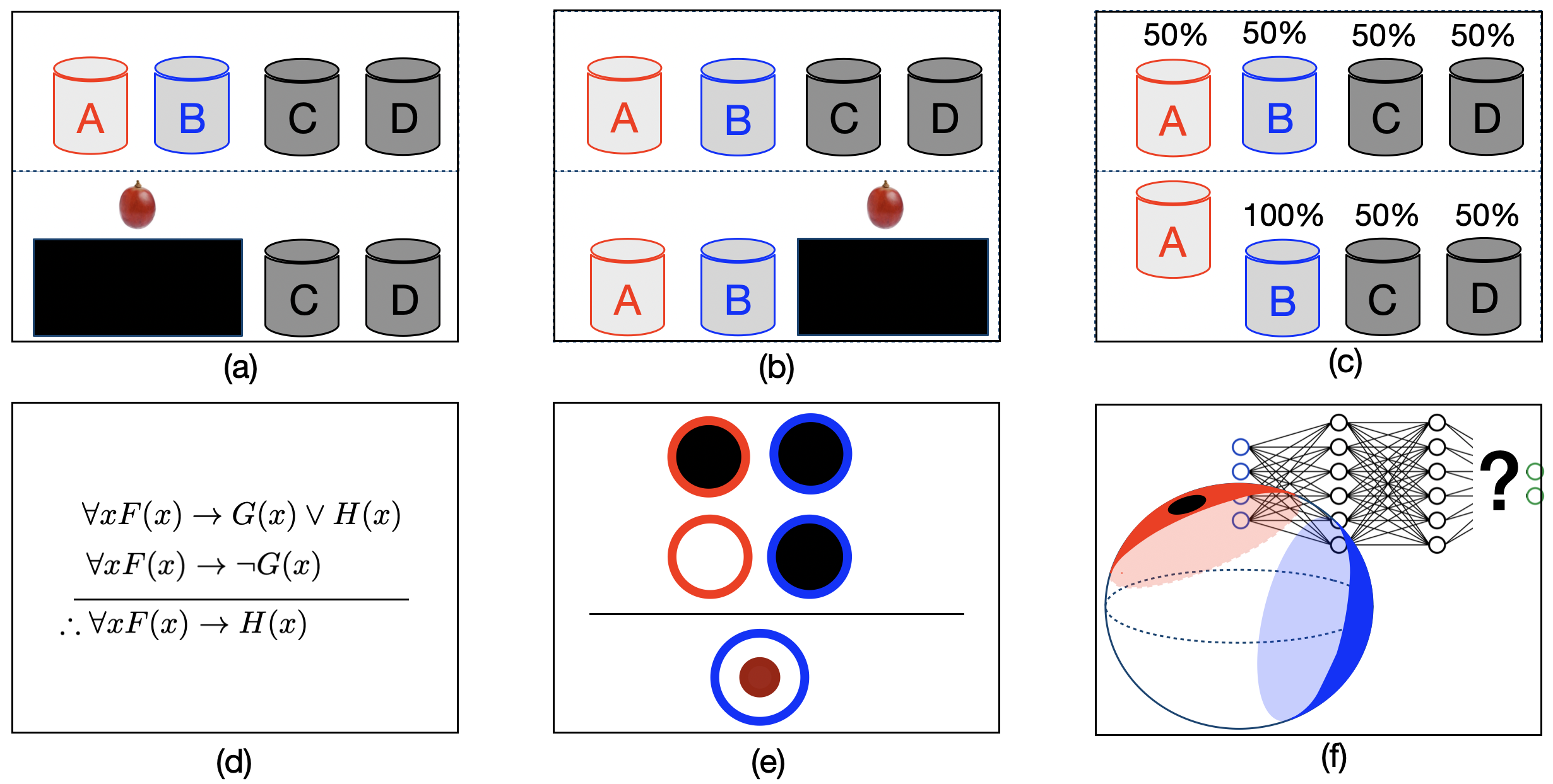
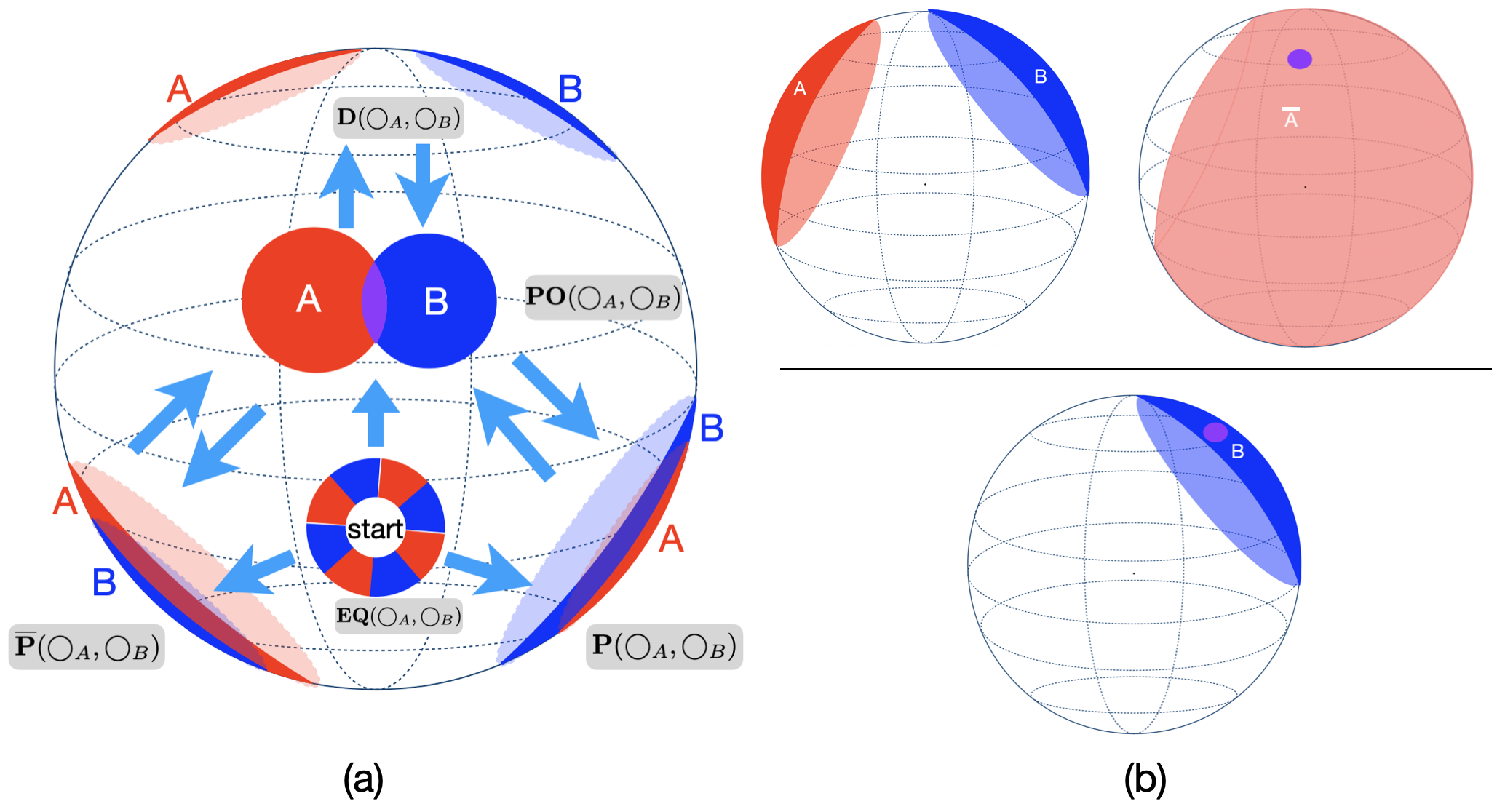
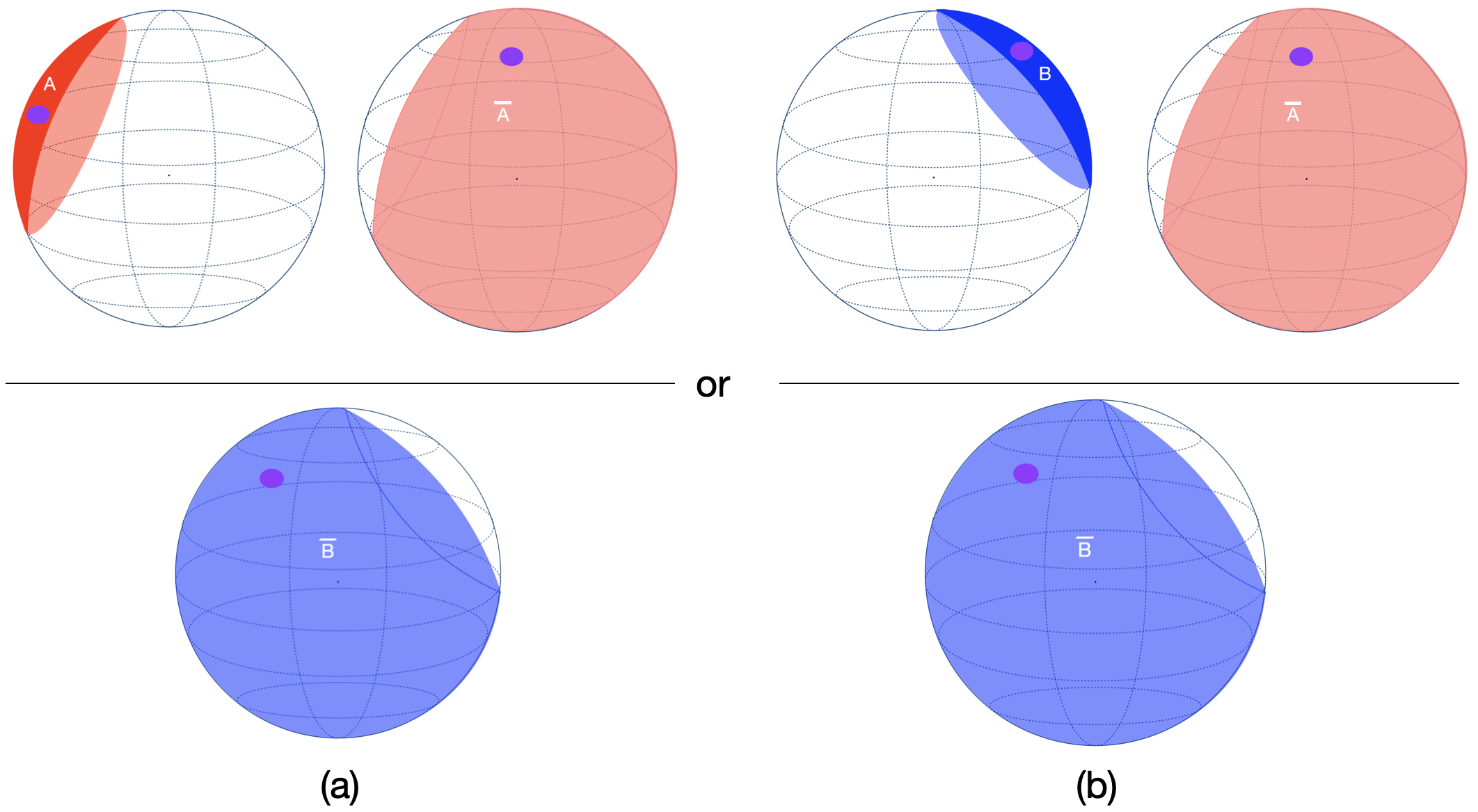
세 번째인 명시적 모델 기반 추론은 논리 규칙 자체를 모델 내부에 명시적으로 구현한다는 점에서 차별화된다. 저자들은 개념을 n차원 구 표면 위의 원(circle)으로 임베딩하고, 부정 연산자를 보완 원(complement circle)으로 표현하는 Sphere Neural Networks를 설계하였다. 이 접근법은 기하학적 제약을 통해 논리적 일관성을 자동으로 검증한다는 장점이 있다. 예를 들어, 두 원이 겹치지 않으면 “A와 B는 동시에 참일 수 없다”는 부정 관계를 자연스럽게 구현한다. 또한, 원이 구 표면에 배치되므로 모든 개념이 동일한 차원적 제한을 받으며, 이는 논리적 충돌을 시각적으로 감지하고 필터링하는 메커니즘으로 작동한다. 실험 결과는 Sphere Neural Network가 16개의 전통적 삼단 논법 과제와 이분법적 삼단 논법을 모두 100 % 정확도로 해결하면서, 기존 Euler Net이 겪었던 재앙적 망각 문제를 회피한다는 점에서 설계의 유효성을 입증한다.

하지만 몇 가지 한계도 존재한다. 첫째, 원 기반 임베딩은 개념 간 관계를 원형 교차점으로만 표현하므로, 복합적인 다중 관계(예: 다중 전제와 결론이 얽힌 복합 논증)를 다루는 데 확장성이 제한될 수 있다. 둘째, 구의 차원을 증가시키면 계산 복잡도가 급격히 상승하는데, 대규모 실세계 데이터에 적용하려면 효율적인 차원 축소 및 근사 기법이 필요하다. 셋째, 현재 실험은 전통적인 형식 논리(삼단 논법)와 그 변형에 국한되어 있어, 비형식적 추론이나 확률적 논리와의 통합 가능성은 아직 검증되지 않았다.

종합하면, 본 논문은 “명시적 모델 기반 추론”이 신뢰성 측면에서 가장 유망함을 실증적으로 보여준다. 특히, 기하학적 구조를 활용한 Sphere Neural Networks는 논리적 일관성을 내재화함으로써 LLM이나 감독 학습 기반 모델이 겪는 불안정성을 효과적으로 보완한다. 향후 연구에서는 복합 논리 구조, 고차원 임베딩 효율성, 그리고 확률적/비형식적 추론과의 융합을 탐색함으로써 이 접근법을 보다 일반화된 인공지능 시스템에 적용할 수 있을 것으로 기대된다.

📄 논문 본문 발췌 (Excerpt)

## AI 원숭이가 포도 선택: 구형 신경망을 통한 신뢰할 수 있는 의사 결정

본 논문은 고위험 응용 분야에서 신뢰할 수 있는 의사 결정이 필수적인 인공지능(AI)의 한계를 탐구하고, 구형 신경망(Sphere Neural Network)이라는 새로운 접근 방식을 소개한다. 전통적인 언어 모델(LLM)은 인간과 유사한 의사소통 및 추론 능력을 보여주지만, 단순한 추론에는 여전히 오류가 발생하며, 설명 가능한 결정을 내리는 데 어려움을 겪는다.

기존 문제점:

LLM의 한계: LLM은 복잡한 단백질 구조 예측이나 기상 예측과 같은 분야에서 뛰어난 성능을 보여주지만, 간단한 추론에는 오류가 발생한다. 예를 들어, Mitchell (2023)은 LLM이 단순한 추론에 있어 여전히 많은 오류를 범한다고 지적했다.
설명 가능한 AI의 부족: LLM의 결정 과정은 블랙박스로 간주되며, 그 결과에 대한 설명이 어렵다. 이는 의료 진단이나 법률 판단과 같은 분야에서 신뢰성을 떨어뜨린다.

구형 신경망(Sphere Neural Network) 소개:

본 논문에서는 구형 신경망을 제안하여 이러한 문제점을 해결하고자 한다. 구형 신경망은 시각적 공간에 원을 배치하는 방식으로 추론을 수행한다. 이 방법은 다음과 같은 장점을 제공한다:

인식 가능한 모델: 구형 신경망은 인간이 이해할 수 있는 시각적 표현을 사용하여 추론 과정을 명확하게 보여준다.
데이터 독립성: 구형 신경망은 사전 학습 데이터에 의존하지 않고, 주어진 전제로부터 직접 결론을 도출한다. 이는 데이터 수집 및 훈련 과정의 비용과 노력을 크게 절감한다.
지속적인 학습: 새로운 지식을 습득하면 기존 모델에 통합되어 지속적으로 학습할 수 있다.
전이 학습 가능성: 구형 신경망에서 학습된 추론 방법은 다른 과제에 직접 적용될 수 있으며, 추가적인 미세 조정 없이도 효과적으로 작동한다.
기호 수준 논리 추론: 구형 신경망은 기호 수준의 논리적 추론을 달성하여 인공지능 연구에서 상징주의와 연결주의의 갈등을 해소하는 새로운 길을 제시한다.

실험 및 결과:

본 논문에서는 다양한 실험을 통해 구형 신경망의 효과를 입증한다. 특히, 다음과 같은 결과를 얻었다:

기존 방법과의 비교: 구형 신경망은 고전적인 추론과 복잡한 추론 모두에서 기존 방법(예: Euler Net)보다 우수한 성능을 보여주었다.
다양한 데이터 패턴에 대한 적응력: 구형 신경망은 입력 패턴의 변화에 잘 적응하며, 특히 불확실성을 나타내는 다양한 시각적 특징을 처리할 수 있다.
고위험 응용 분야의 잠재력: 구형 신경망은 의료 진단, 법률 판단과 같은 고위험 응용 분야에서 신뢰할 수 있는 의사 결정을 내리는 데 활용될 수 있다.

결론:

본 논문은 구형 신경망을 통해 AI 시스템이 인간과 유사한 방식으로 신뢰할 수 있고 설명 가능한 의사 결정을 내릴 수 있음을 보여주었다. 이 연구는 인공지능의 미래를 형성하는 데 중요한 기여를 할 것으로 기대된다.

📄 ArXiv 원문 PDF 보기