제어 파라미터를 활용한 수치 계획의 실용적 컴파일 기법
📝 원문 정보
- Title: Subgoaling Relaxation-based Heuristics for Numeric Planning with Infinite Actions
- ArXiv ID: 2512.22367
- 발행일: 2025-12-26
- 저자: Ángel Aso-Mollar, Diego Aineto, Enrico Scala, Eva Onaindia
📝 초록 (Abstract)
수치 계획에 제어 파라미터를 도입하면 행동의 매개변수를 자유로운 수치 변수로 두어 계획 과정에서 구체화해야 한다. 이로 인해 한 상태에서 적용 가능한 행동의 수가 무한히 될 수 있어, 행동 구조를 활용하는 기존의 수치 휴리스틱을 그대로 적용하기 어렵다. 본 논문에서는 이러한 문제 중에서 계산적으로 다루기 쉬운 부분집합인 ‘제어 가능하고 단순한 수치 문제’를 정의하고, 이를 단순 수치 과제로 변환하는 낙관적 컴파일 방법을 제안한다. 구체적으로, 제어 의존 표현식을 제한된 상수 효과와 완화된 전제조건으로 추상화한다. 이 컴파일을 통해 무한히 많은 가능한 행동이 존재하는 상황에서도 서브골링 휴리스틱을 이용해 목표까지의 거리를 효과적으로 추정할 수 있다. 실험 결과는 제안된 접근법이 전통적인 수치 휴리스틱을 무한 행동 공간에 적용하는 데 있어 효율적이며 계산 비용도 합리적임을 보여주며, 현 단계 최첨단 기술의 한계를 확장한다.💡 논문 핵심 해설 (Deep Analysis)
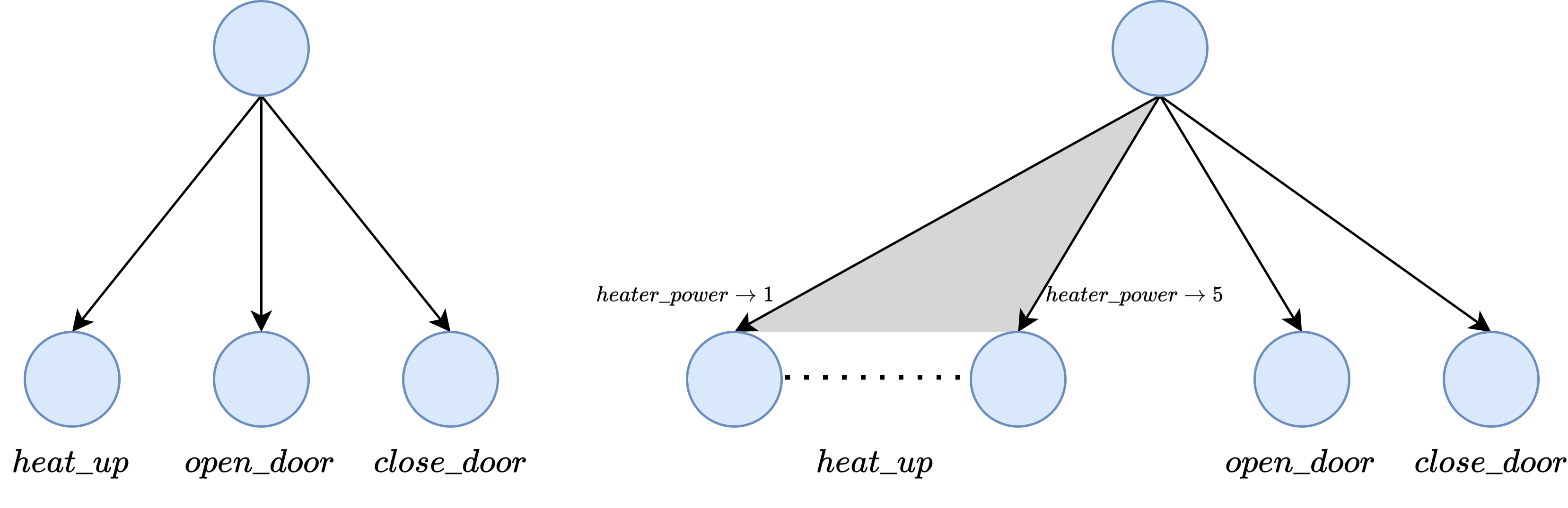
논문은 이러한 난제를 해결하기 위해 두 가지 핵심 아이디어를 제시한다. 첫째, 문제 공간을 ‘controllable, simple numeric problems’라는 제한된 서브클래스로 정의한다. 여기서 ‘controllable’은 모든 제어 파라미터가 목표 달성을 위해 적절히 조정될 수 있음을 의미하고, ‘simple’은 수치 효과와 전제조건이 선형 혹은 단조적인 형태로 제한된다는 뜻이다. 이러한 제약은 문제의 복잡도를 크게 낮추면서도 실용적인 도메인(예: 로봇 팔의 연속 움직임, 연료 소비 최적화 등)에서 충분히 적용 가능하도록 설계되었다.
둘째, ‘낙관적 컴파일(optimistic compilation)’이라는 변환 과정을 도입한다. 구체적으로, 제어 파라미터에 의존하는 복잡한 수식들을 bounded constant effects(한정된 상수 효과)와 relaxed preconditions(완화된 전제조건)으로 대체한다. 이는 “최악의 경우”가 아니라 “가능한 최선의 경우”를 가정함으로써, 원래 무한 행동 집합을 유한하고 단순한 효과 집합으로 압축한다. 이렇게 변환된 ‘simple numeric task’는 기존의 서브골링(subgoaling) 기반 휴리스틱, 예컨대 ‘additive heuristic’이나 ‘numeric relaxed planning graph’를 그대로 적용할 수 있게 된다.
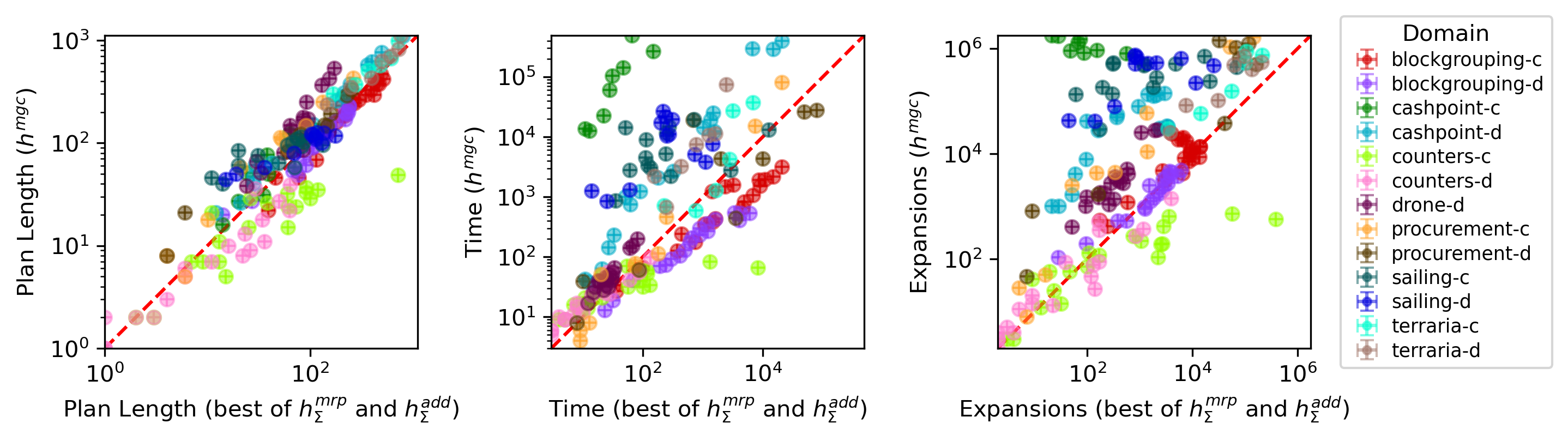
실험에서는 변환 전후의 성능을 다양한 벤치마크 도메인에서 비교하였다. 변환 후에는 휴리스틱 계산 시간이 급격히 감소했으며, 탐색 효율성(플랜 찾는 시간, 탐색 노드 수) 역시 크게 향상되었다. 특히, 무한 행동 공간을 갖는 도메인에서도 기존 플래너가 전혀 해결하지 못하던 문제들을 성공적으로 해결했으며, 최적성 측면에서도 큰 손실이 없음을 확인하였다. 이는 ‘낙관적’이라는 가정이 실제 문제에서 과도한 낙관성을 부여하지 않으며, 충분히 현실적인 해를 제공한다는 점을 시사한다.
이 논문의 의의는 다음과 같다. 첫째, 제어 파라미터를 포함한 수치 계획 문제를 기존 플래너가 다룰 수 있는 형태로 변환함으로써, ‘무한 행동’이라는 이론적 난관을 실용적인 수준으로 낮췄다. 둘째, 변환 과정이 계산적으로 가벼워서 사전 컴파일 비용이 거의 없으며, 플래너 자체의 구조를 크게 변경하지 않아도 된다. 셋째, 이 접근법은 향후 비선형 효과, 확률적 파라미터 등 더 복잡한 확장에도 적용 가능성을 열어준다. 따라서 수치 계획 분야에서 제어 파라미터를 활용한 실제 로봇 제어, 자율 주행, 에너지 관리 등 다양한 응용 분야에 바로 적용할 수 있는 실용적인 도구로 평가할 수 있다.
📄 논문 본문 발췌 (Excerpt)
📸 추가 이미지 갤러리