연속 행동 공간에서 가우시안 프로세스 회귀를 활용한 루트 병렬 MCTS 통계 통합

2025년 12월 10일

읽는 시간: 5 분

...

📝 원문 정보

Title: Gaussian Process Aggregation for Root-Parallel Monte Carlo Tree Search with Continuous Actions
ArXiv ID: 2512.09727
발행일: 2025-12-10
저자: Junlin Xiao, Victor-Alexandru Darvariu, Bruno Lacerda, Nick Hawes

📝 초록 (Abstract)

Monte Carlo Tree Search(MCTS)는 온라인 계획의 핵심 알고리즘으로, 시간 제약이 있지만 최상의 성능을 원하는 상황에서 루트 병렬 변형이 널리 사용됩니다. 연속적인 행동 공간 환경에서는 여러 스레드로부터 얻은 통계를 어떻게 가장 잘 통합할지에 대한 질문은 중요한 문제지만, 아직 충분히 탐구되지 않았습니다. 본 연구에서는 가우시안 프로세스 회귀를 활용하여 환경에서 시도되지 않은 유망한 행동의 가치 추정치를 얻는 방법을 제안합니다. 우리는 6개의 다른 도메인에 걸쳐 체계적인 평가를 수행하고, 우리의 접근법이 기존의 통합 전략보다 우수하며, 추론 시간은 소폭 증가하는 것을 보여줍니다.

💡 논문 핵심 해설 (Deep Analysis)

Analysis of the Paper “Utilizing Gaussian Process Regression for Statistical Integration in Root Parallel MCTS in Continuous Action Spaces”

Introduction:

The paper introduces a novel method called GPR2P (Gaussian Process Regression for Root Parallel Monte Carlo Tree Search) to enhance statistical integration within root parallel Monte Carlo Tree Search (MCTS). The authors highlight that while MCTS is widely used due to its anytime applicability and effectiveness in planning under time or simulation budget constraints, its performance heavily relies on the quality of simulation results. This reliance can lead to difficulties in identifying strong actions when resources are limited.

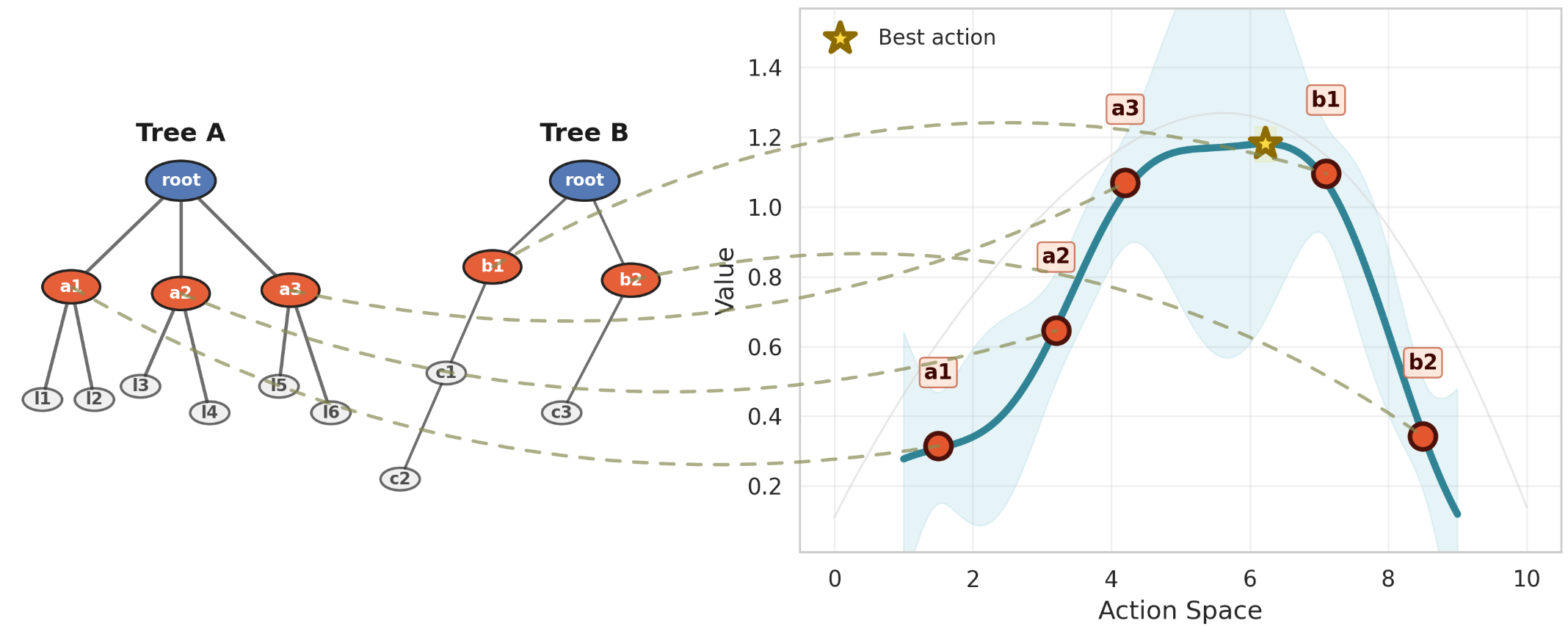
Root Parallel MCTS improves upon traditional MCTS by running multiple independent MCTS instances and integrating their outcomes to select a final action. However, an optimal method for aggregating these results remains a significant challenge, especially in continuous action spaces where each sampled action is unique, making conventional majority voting approaches ineffective.

Existing Methods vs. GPR2P:

The authors compare existing methods used for statistical integration within root parallel MCTS with their proposed GPR2P approach:

Max Algorithm: Selects the state-action pair with the highest estimated value.
Most Visited Algorithm: Chooses the action that has been visited most frequently.

Kurzer, Hörtnagl, and Zöllner (2020) introduced two methods for integrating all trees using action similarity: Similarity Vote and Similarity Merge. These methods use an Euclidean distance-based similarity matrix to establish connections between actions.

GPR2P differs from these existing approaches by constructing a statistical model over the entire action space, thereby expanding the selection range beyond just sampled actions. It applies a visitation threshold τ to filter out sufficiently explored actions and performs Gaussian Process Regression (GPR) on these filtered actions.

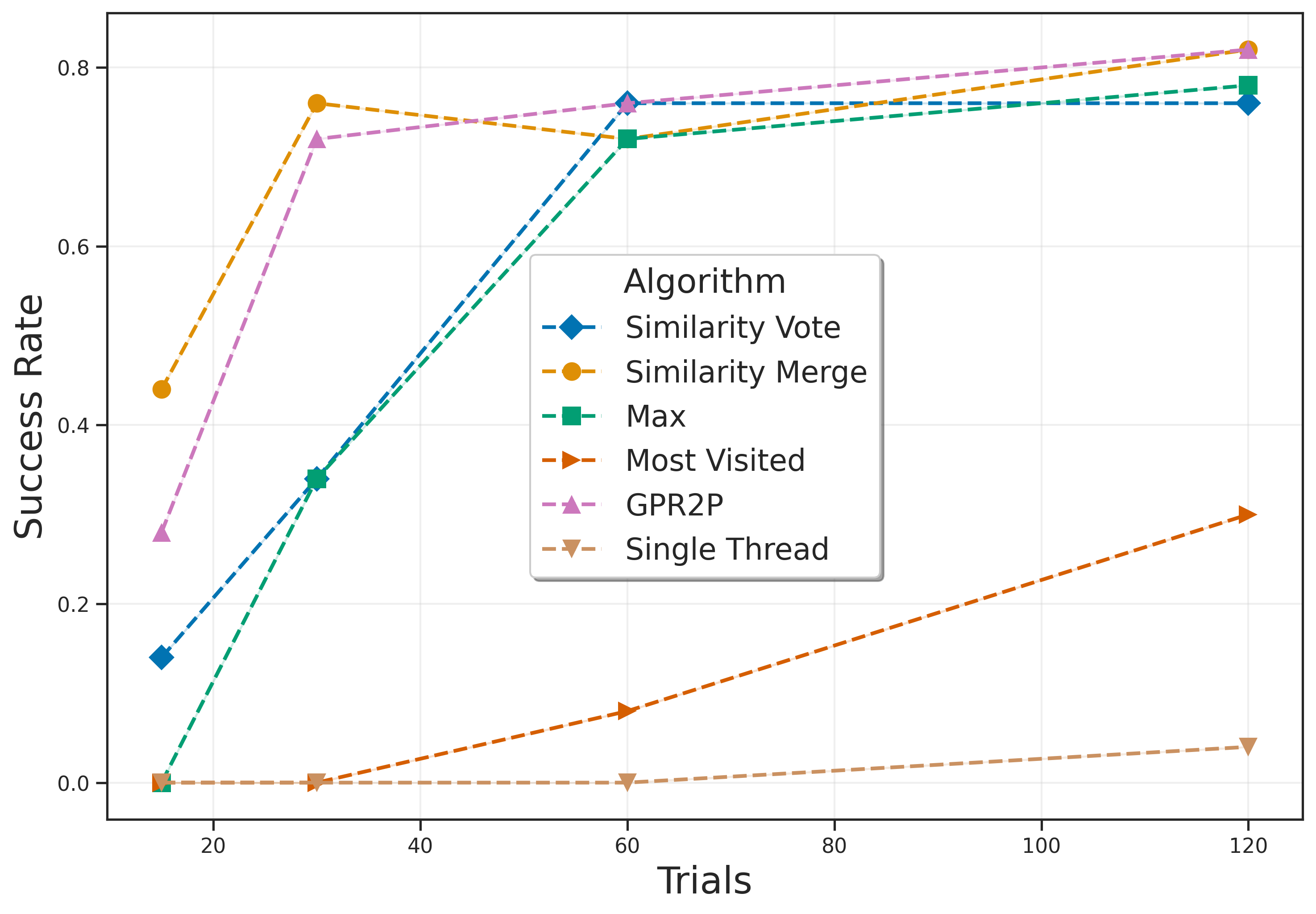
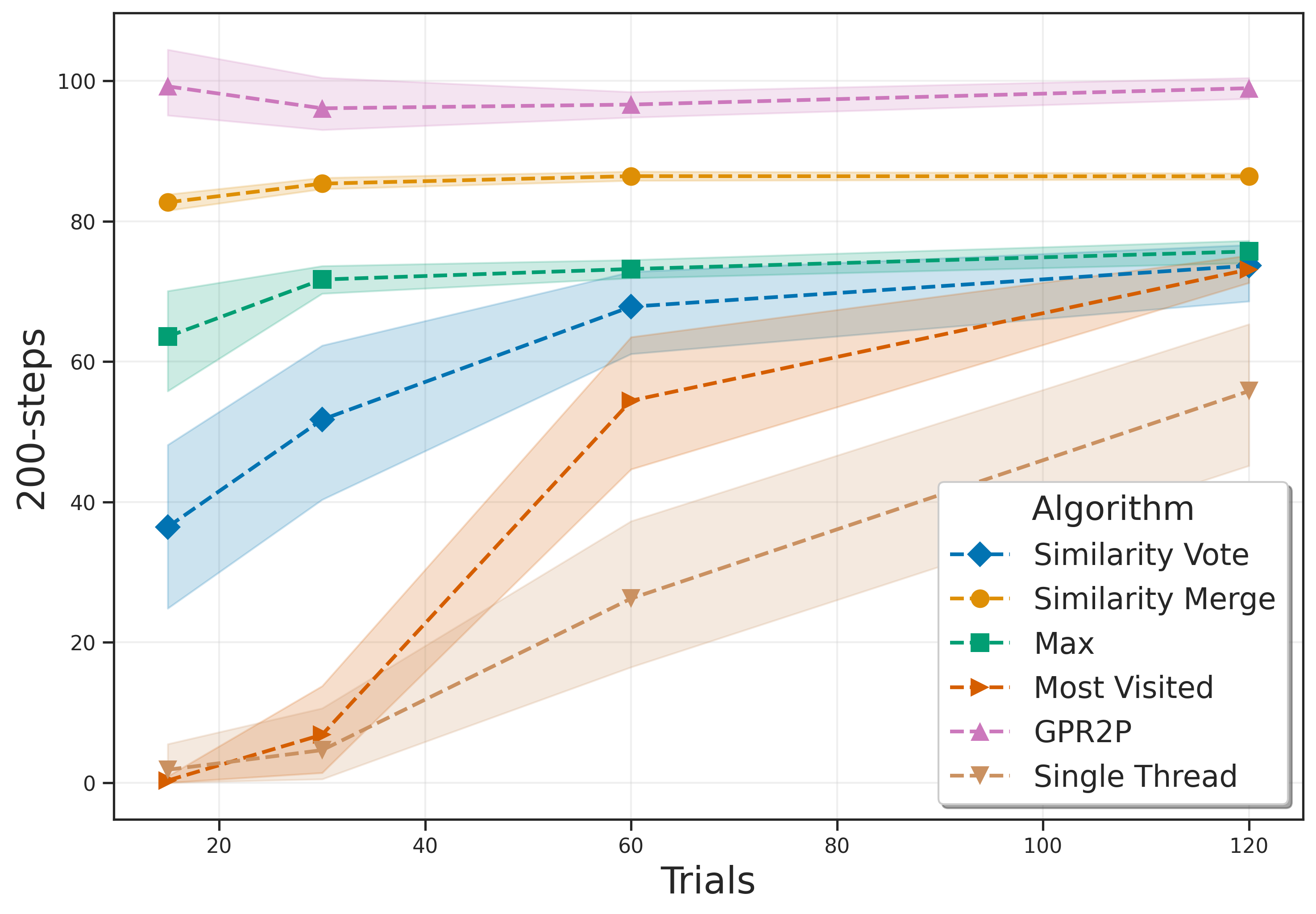
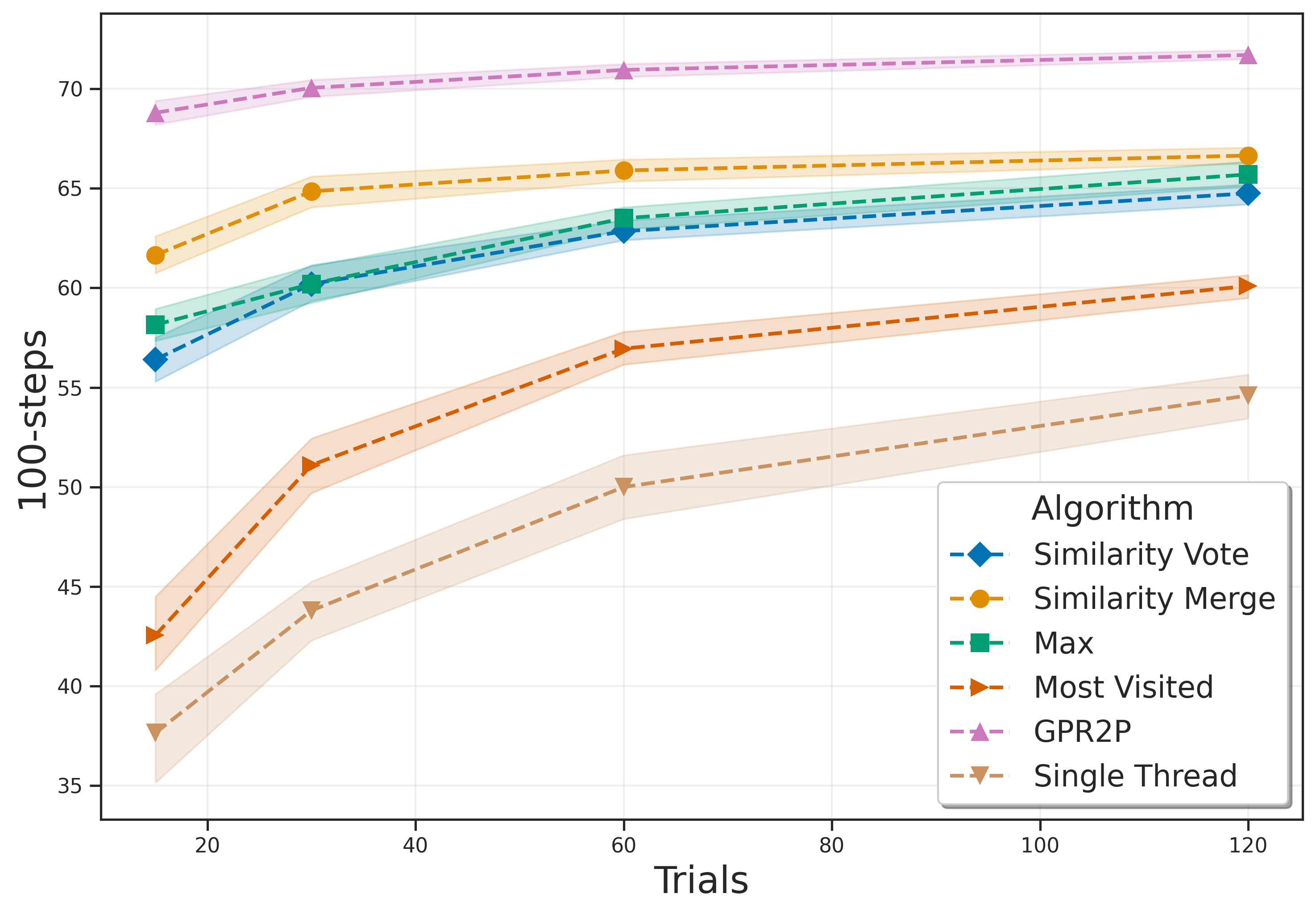
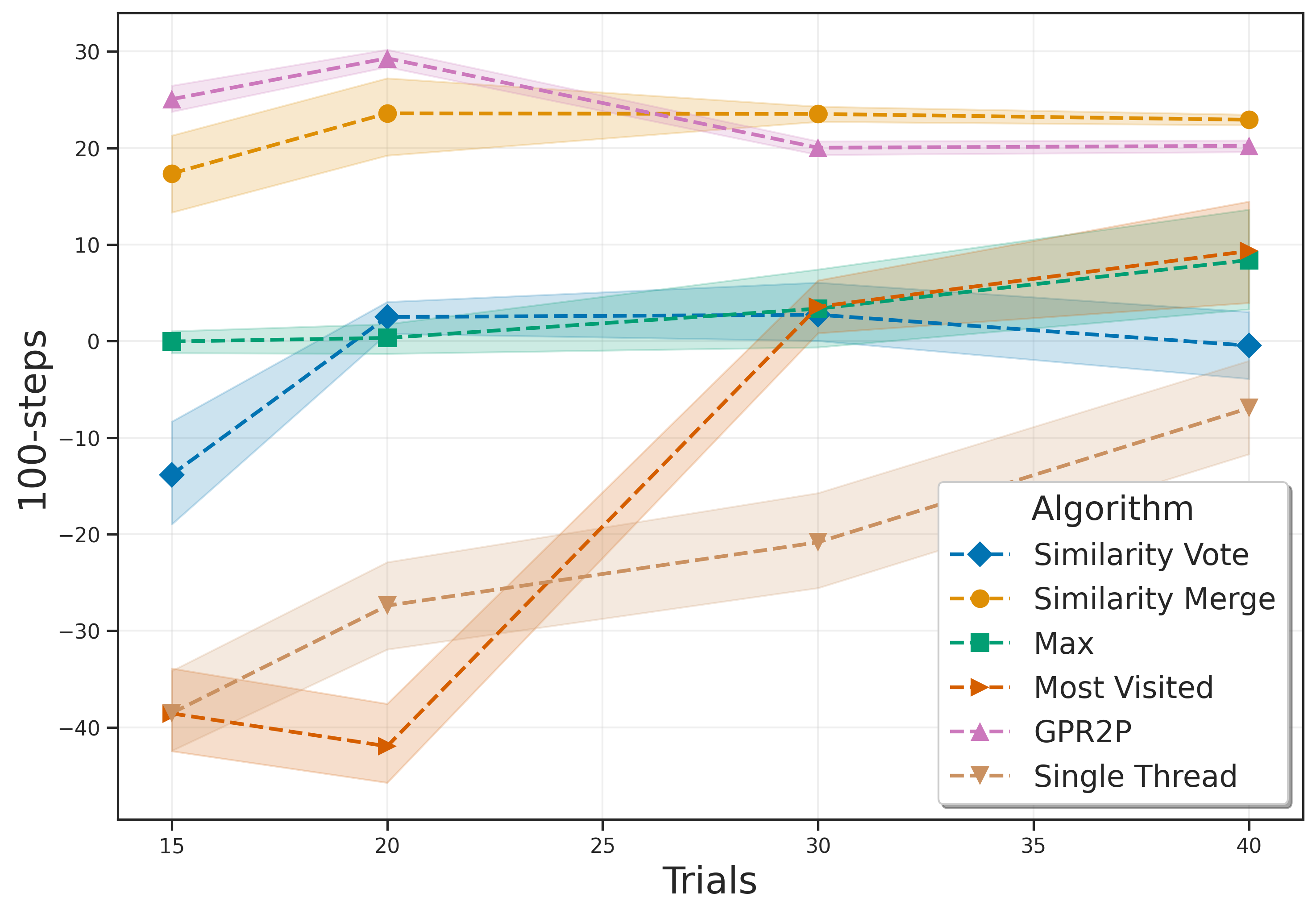
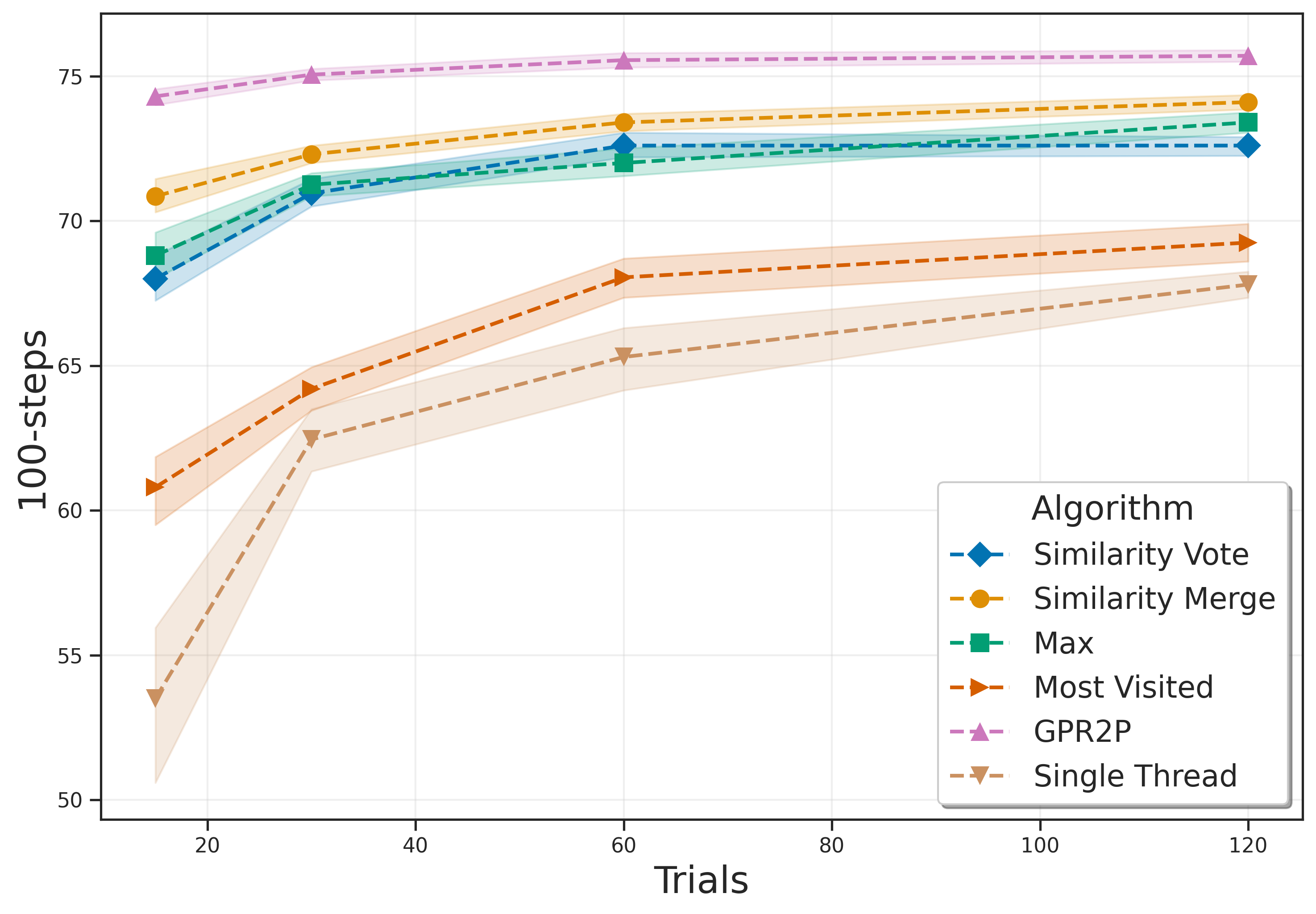
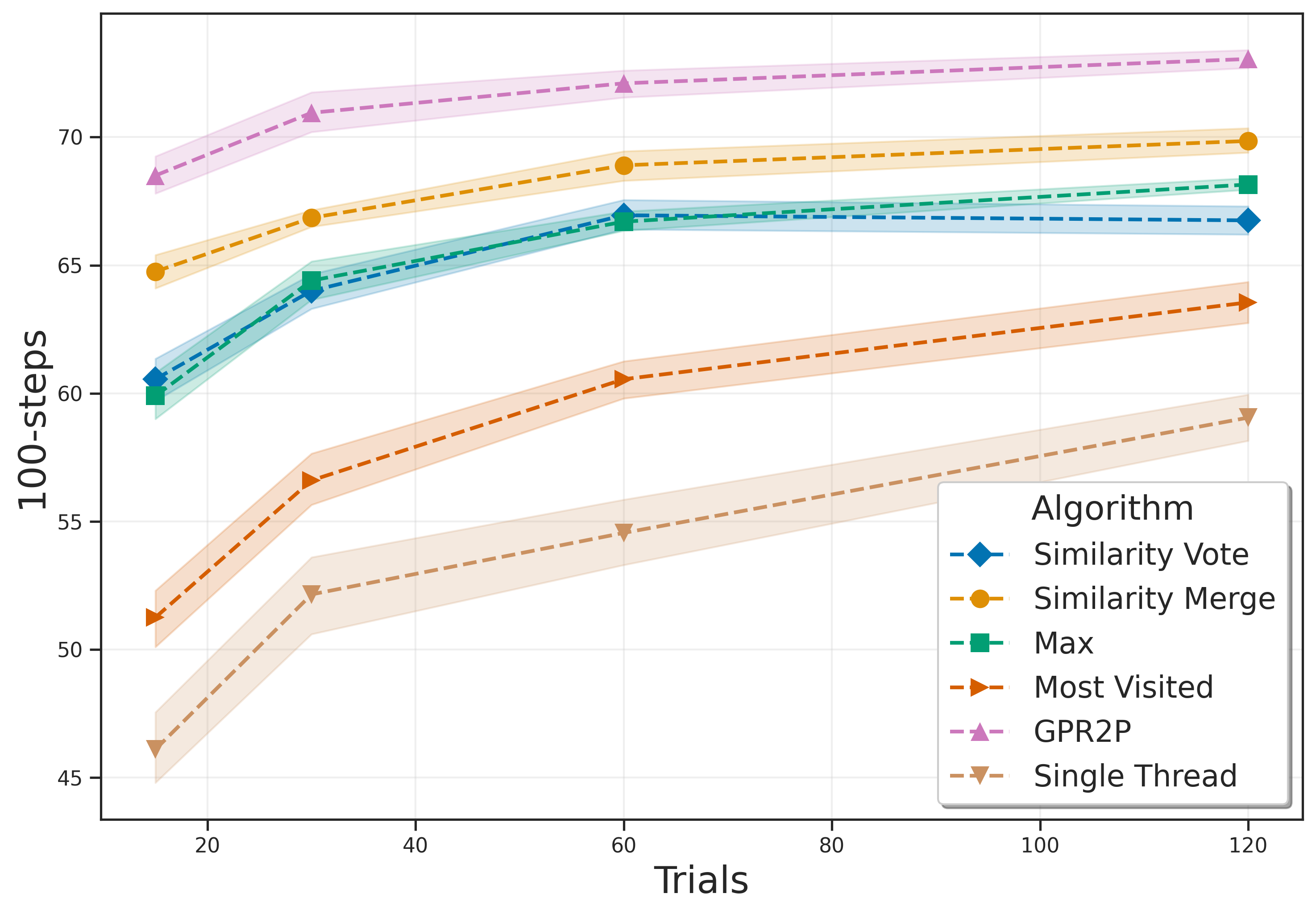
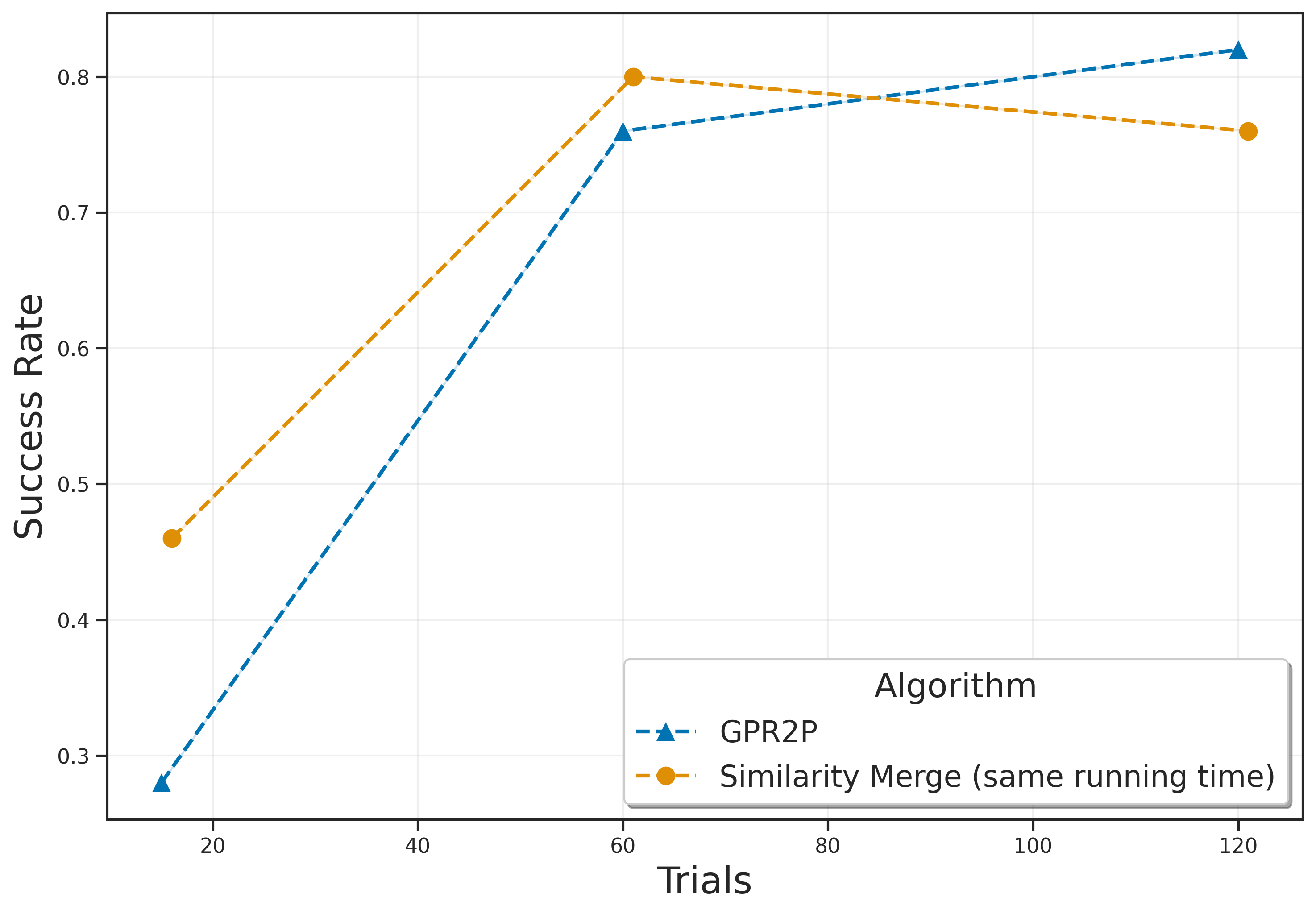
Experiments and Results:

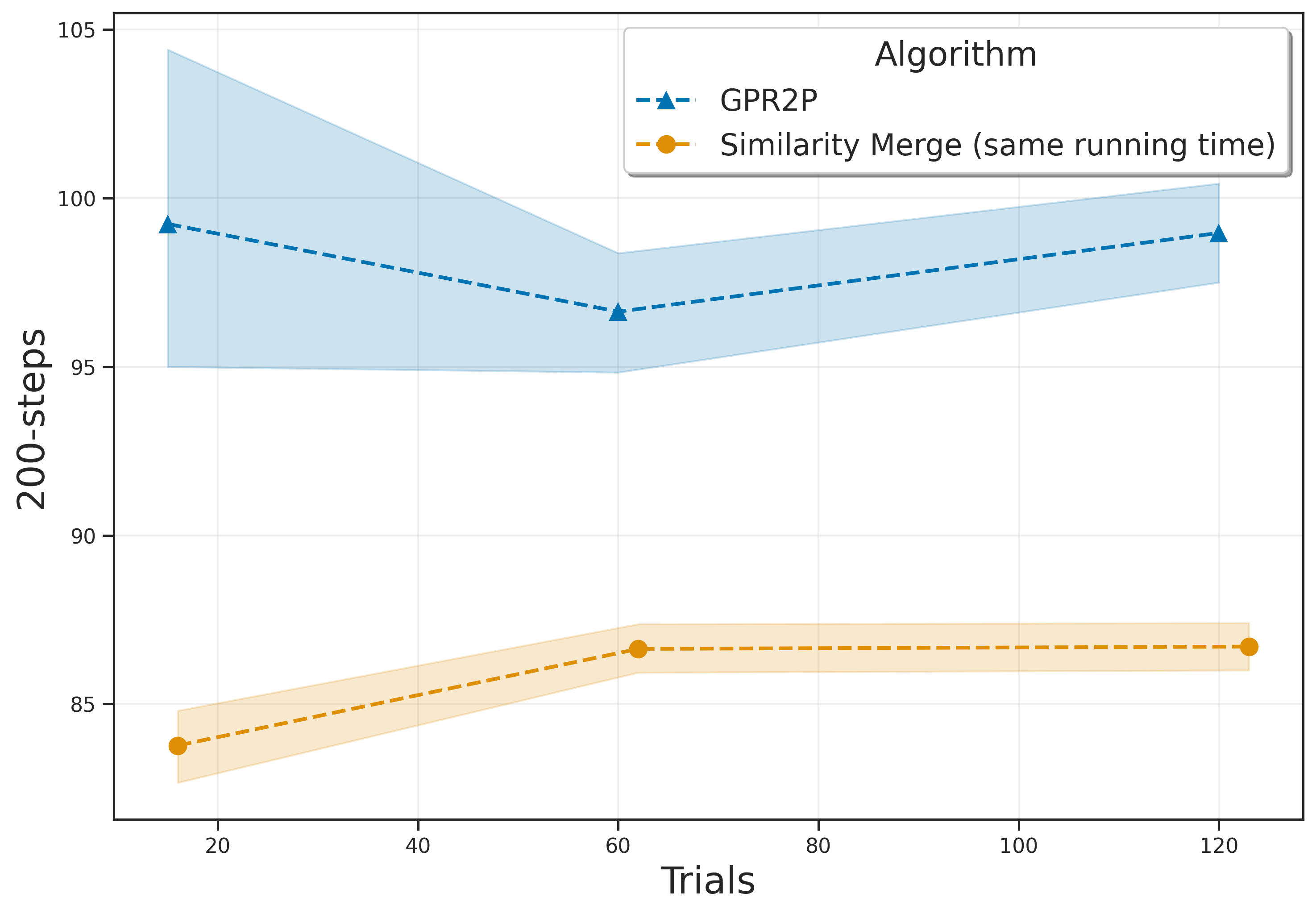
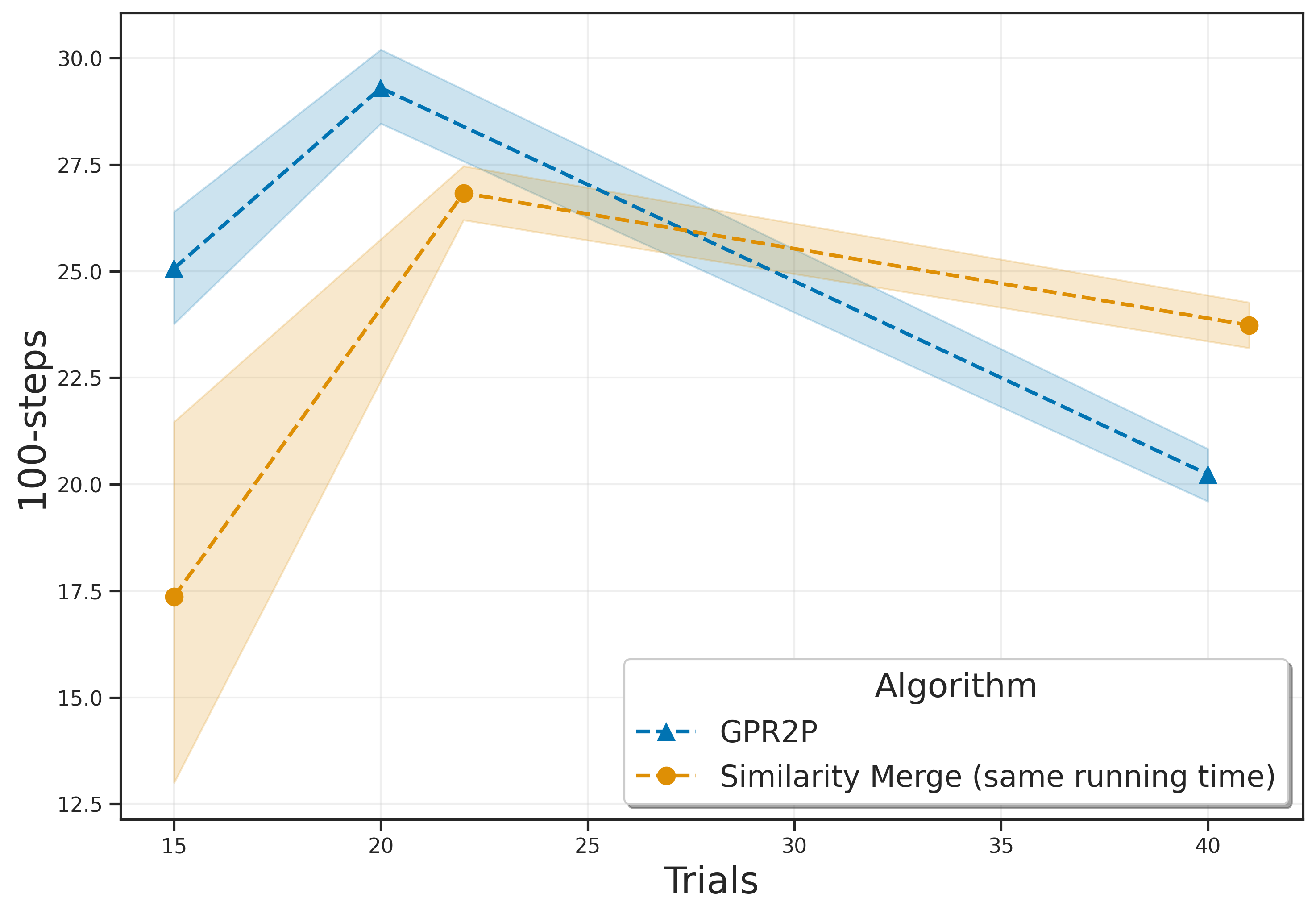
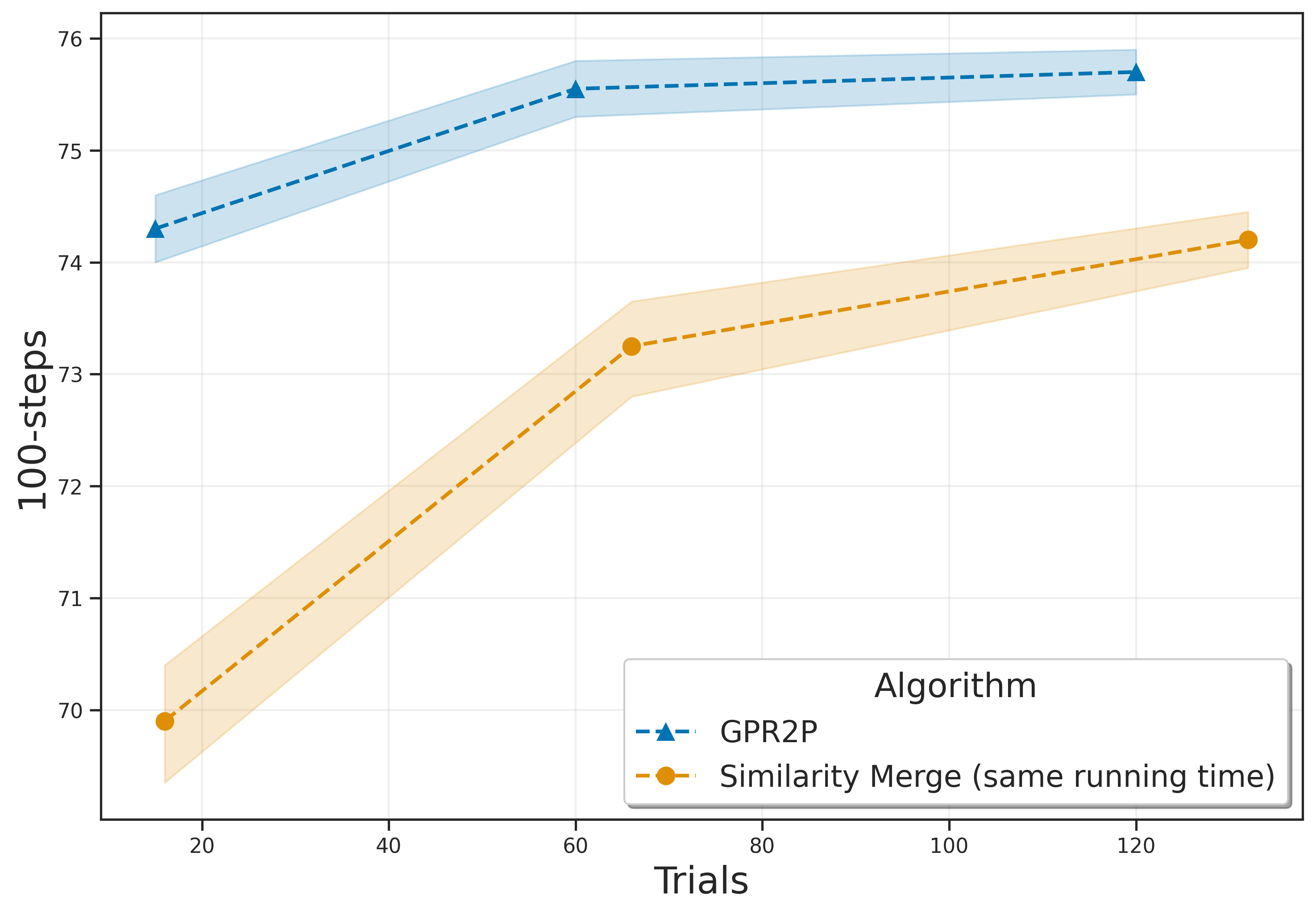
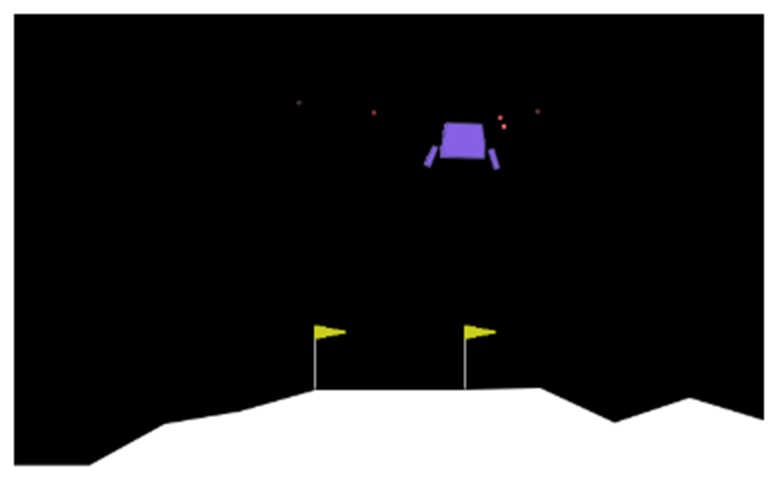
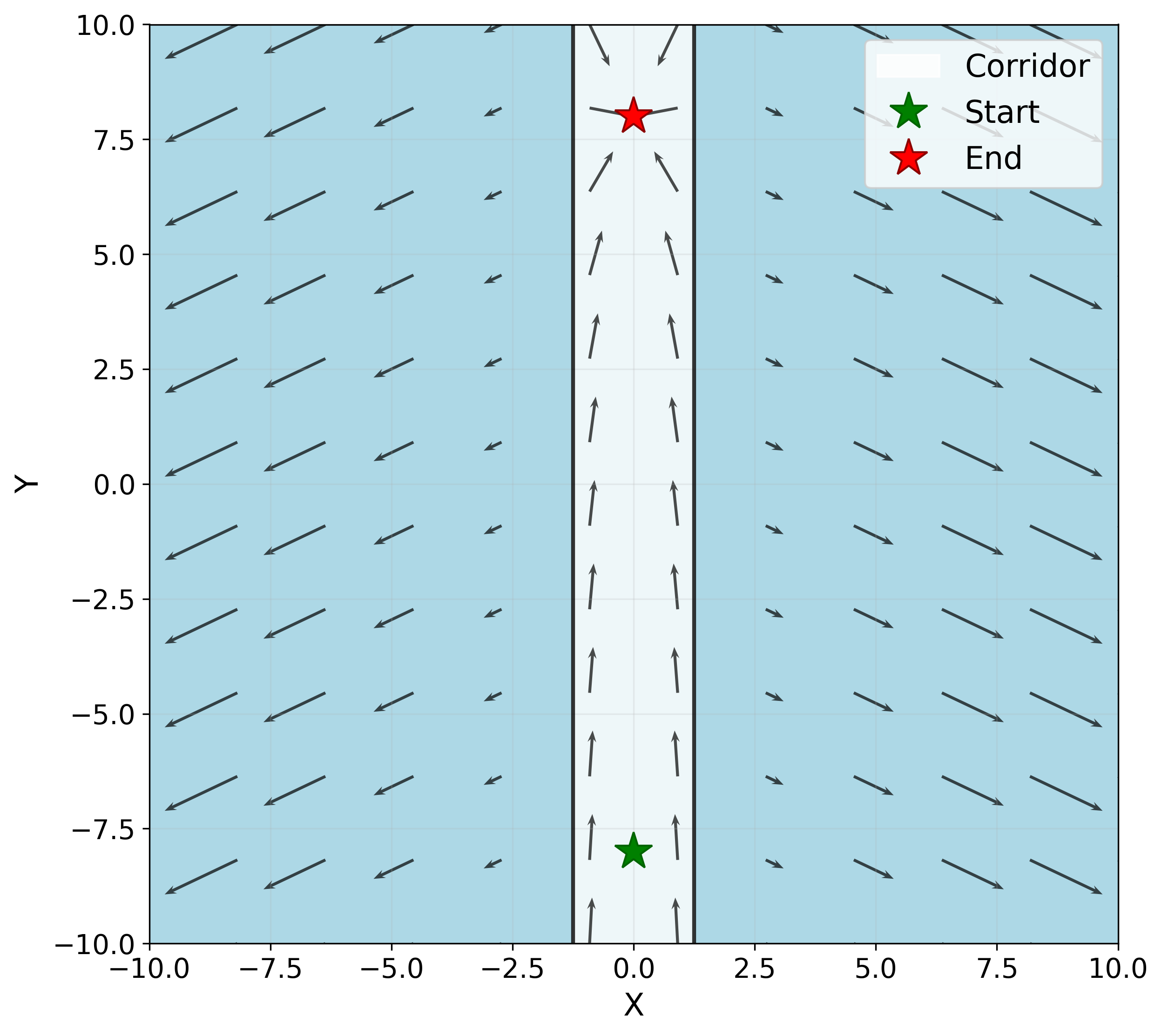
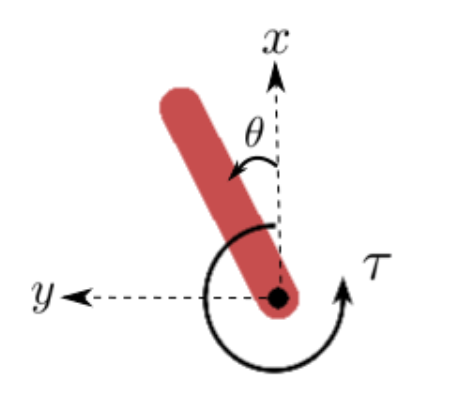
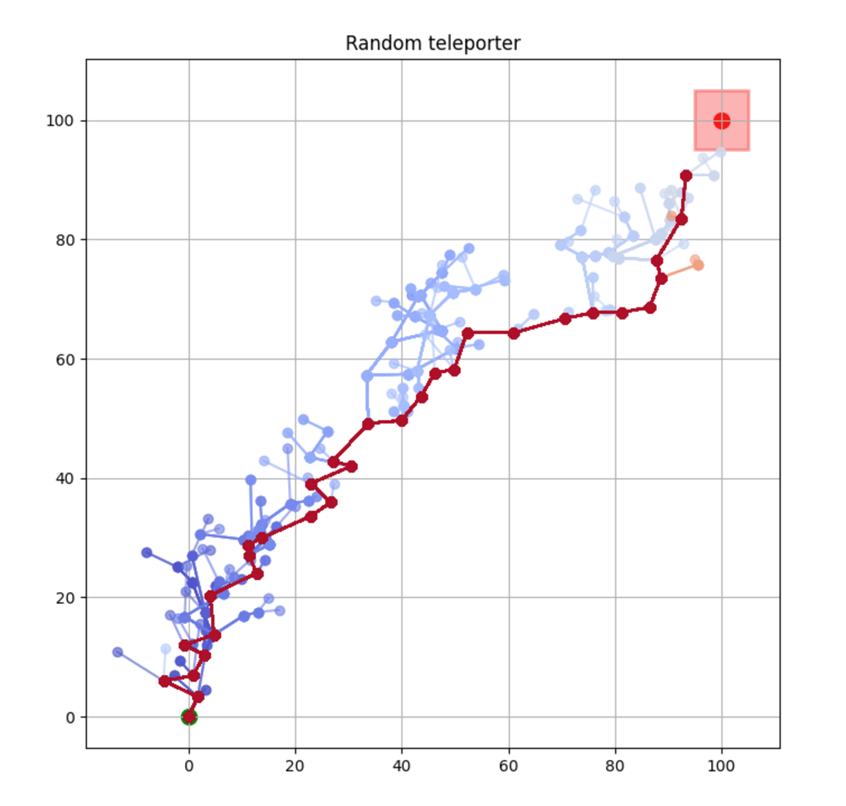
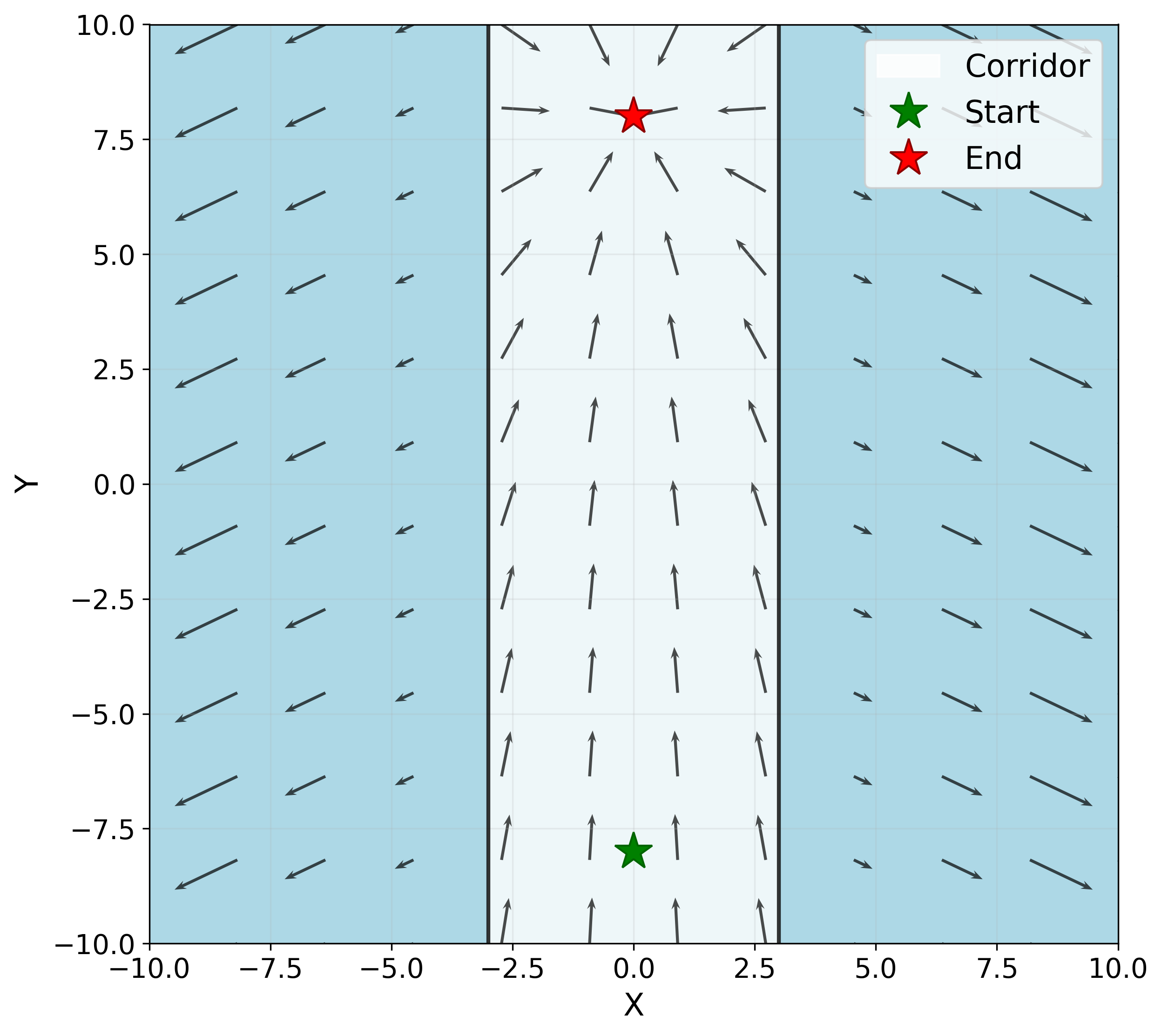
The authors conducted experiments in six different environments: Lunar Lander, Mountain Car, Pendulum, Random Teleporter, Wide Corridor, and Narrow Corridor. The results indicate that GPR2P consistently outperforms both existing methods and single-threaded MCTS across all environments. Notably, GPR2P showed better performance compared to Similarity Merge, with the performance gap decreasing as the number of simulations increased.

Conclusion:

The paper proposes a new method called GPR2P for improving statistical integration in root parallel MCTS by utilizing Gaussian Process Regression. Experimental results demonstrate that GPR2P outperforms existing methods across various environments. Future research directions include further enhancing the efficiency of GPR2P and exploring its application in diverse fields.

Summary:

The paper presents a significant advancement in the field of Monte Carlo Tree Search, particularly for continuous action spaces. By leveraging Gaussian Process Regression, GPR2P offers a more robust method for integrating results from multiple MCTS instances, leading to improved performance across different environments. This research not only enhances the capabilities of root parallel MCTS but also opens up new avenues for its application in complex decision-making scenarios.

📄 논문 본문 발췌 (Excerpt)

## [연속 행동 공간에서의 루트 병렬 MCTS 통계 통합을 위한 가우시안 프로세스 회귀 활용] 전문 번역

서론:

Monte Carlo Tree Search (MCTS)는 온라인 계획 알고리즘으로서 널리 사용되고 있습니다. 시간 제약이나 시뮬레이션 예산에 관계없이 효과적으로 계획을 수립할 수 있는 언제든지 실행 가능한 특성을 지닙니다. 이러한 장점에도 불구하고, MCTS의 성능은 시뮬레이션 결과의 품질에 크게 의존하며, 제한된 자원에서는 강력한 행동을 식별하는 데 어려움을 겪을 수 있습니다.

루트 병렬 MCTS (Cazenave and Jouandeau 2007)는 독립적인 MCTS 실행을 수행하고 결과를 통합하여 최종 행동을 선택하는 방법입니다. 이는 특히 시간이나 계산 자원이 제한적인 경우 성능을 향상시킵니다. 그러나 루트 병렬 MCTS의 효과적인 결과 집계를 위한 최적의 방법은 여전히 중요한 과제로 남아 있습니다. 특히, 연속 행동 공간에서는 각 샘플링된 행동이 고유하기 때문에 일반적인 다수결 투표 접근 방식은 적용할 수 없습니다.

본 논문에서는 가우시안 프로세스 회귀 (GPR)를 활용하여 루트 병렬 MCTS의 통계 통합을 개선하는 새로운 방법인 GPR2P를 제안합니다. GPR2P는 단순히 샘플링된 행동만 고려하는 기존 접근 방식과 달리, 전체 행동 공간에 대한 통계적 모델을 구축하여 더 나은 성능을 달성합니다. 이는 제한적인 시뮬레이션 예산이나 우수한 행동을 발견하기 어려운 상황에서 특히 중요합니다.

기존 방법 및 GPR2P:

루트 병렬 MCTS는 모든 스레드에서 독립적으로 몬테카를로 트리를 생성하고, 그 결과를 통합하여 최종 행동을 선택합니다. 통합된 정보에는 각 상태-행동 쌍의 추정 가치와 방문 횟수가 포함됩니다. 기존 방법은 다음과 같은 두 가지 범주로 분류할 수 있습니다:

Max 알고리즘: 가장 높은 가치를 가진 상태-행동 쌍을 선택합니다.
Most Visited 알고리즘: 방문 횟수가 가장 많은 행동을 선택합니다.

Kurzer, Hörtnagl, and Zöllner (2020)은 행동 유사성을 이용하여 모든 트리를 통합하는 두 가지 방법을 제안했습니다: Similarity Vote와 Similarity Merge입니다. 이러한 방법들은 Euclidean 거리 기반의 유사성 행렬을 사용하여 행동 간의 연결을 설정합니다.

GPR2P는 기존 방법들과 달리 전체 행동 공간에 대한 통계 모델을 구축하여 선택 범위를 확장합니다. GPR2P는 방문 횟수 임계값 τ를 적용하여 충분히 탐색된 행동을 필터링하고, 이러한 행동들에 대해 가우시안 프로세스 회귀 (GPR)를 수행합니다.

실험 및 결과:

여섯 가지 환경에서 GPR2P, 기존 방법, 그리고 단일 스레드 MCTS의 성능을 비교했습니다. 실험 환경은 Lunar Lander, Mountain Car, Pendulum, Random Teleporter, Wide Corridor, Narrow Corridor입니다.

GPR2P는 모든 환경에서 일관되게 가장 높은 성능을 보여주었습니다. 특히, GPR2P는 Similarity Merge에 비해 더 나은 성능을 보였으며, 차이는 시뮬레이션 횟수가 증가함에 따라 감소했습니다.

결론:

본 연구에서는 루트 병렬 MCTS의 통계 통합을 개선하기 위해 가우시안 프로세스 회귀를 활용한 새로운 방법인 GPR2P를 제안했습니다. 실험 결과, GPR2P는 다양한 환경에서 기존 방법에 비해 우수한 성능을 보여주었습니다. 향후 연구 방향으로는, GPR2P의 효율성을 더욱 향상시키고 다양한 응용 분야에 적용할 수 있는 가능성을 탐구하는 것입니다.

📄 ArXiv 원문 PDF 보기