복소수스텝적분변환 고정밀수치미분과스펙트럼분석을위한새로운프레임워크
📝 원문 정보
- Title: The Complex-Step Integral Transform
- ArXiv ID: 2512.09459
- 발행일: 2025-12-10
- 저자: Rafael Abreu, Stephanie Durand, Jochen Kamm, Christine Thomas, Monika Pandey
📝 초록 (Abstract)
Hilbert 변환과 미분 연산자 사이의 잘 알려진 연관성을 기반으로 하고, 최근 복소수 스텝 차분법의 발전에 동기를 얻어 우리는 복소수스텝적분변환(CSIT)을 제안한다. CSIT는 해석적 연속, 미분 근사, 다중 스케일 평활화를 하나의 통합 프레임워크로 결합한 일반화된 적분 변환이다. 스펙트럼 분석 결과, CSIT는 위상은 보존하면서 고파수 잡음을 억제하여 전통적인 Fourier 미분보다 우수한 특성을 보인다. 실수와 허수 스텝 파라미터의 역할을 논의하고, FFT 기반 구현과 보간 기반 구현을 비교하였다. CSIT를 대류 방정식과 순간 주파수 계산에 적용한 결과, Hilbert 기반 방법에 비해 더 부드럽고 강인한 특성을 제공함을 확인했으며, PDE 해석기에 내재된 안정화 효과도 확인하였다. 따라서 CSIT는 수치 미분, 스펙트럼 분석, 지진 신호 처리 등에 유연한 대안이 된다. 향후 비주기적 구현, 적응형 파라미터 선택, 고차 유한요소와 같은 지역 보간 프레임워크와의 통합 등 다양한 연구 방향이 제시된다.💡 논문 핵심 해설 (Deep Analysis)
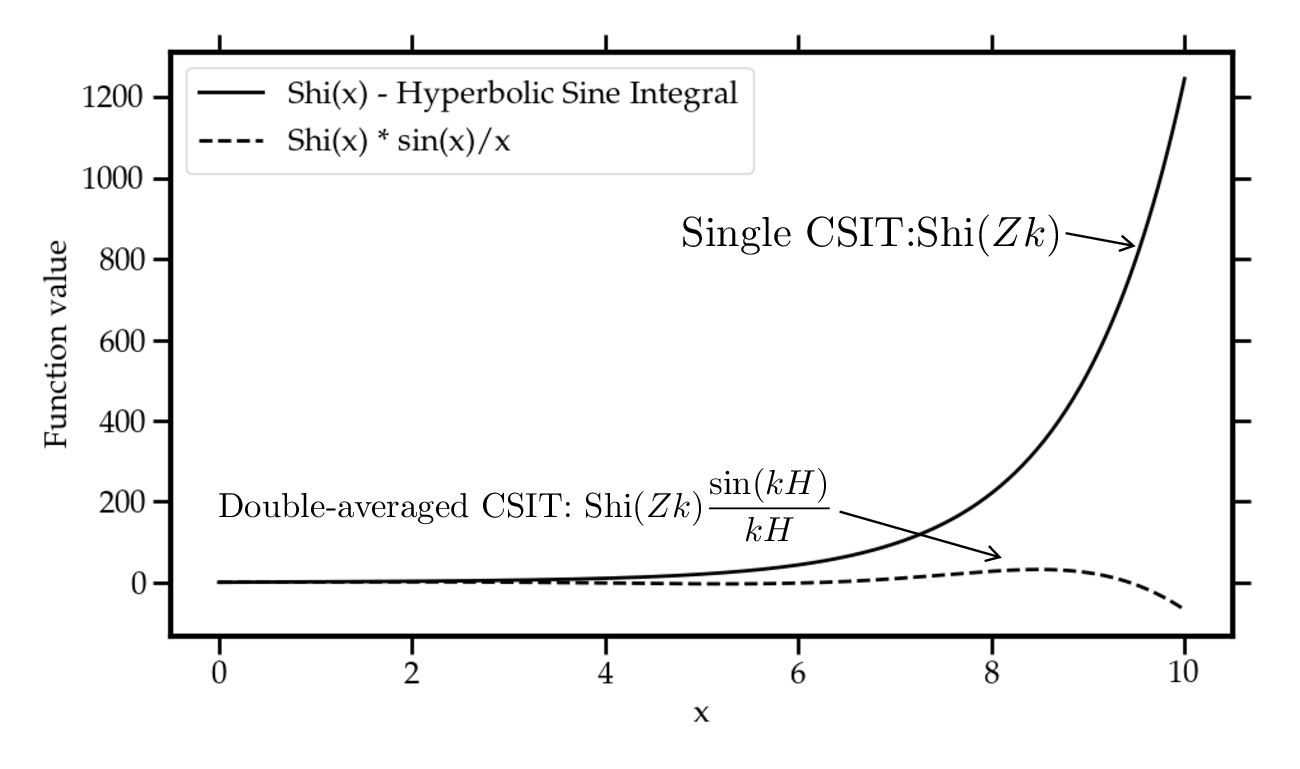
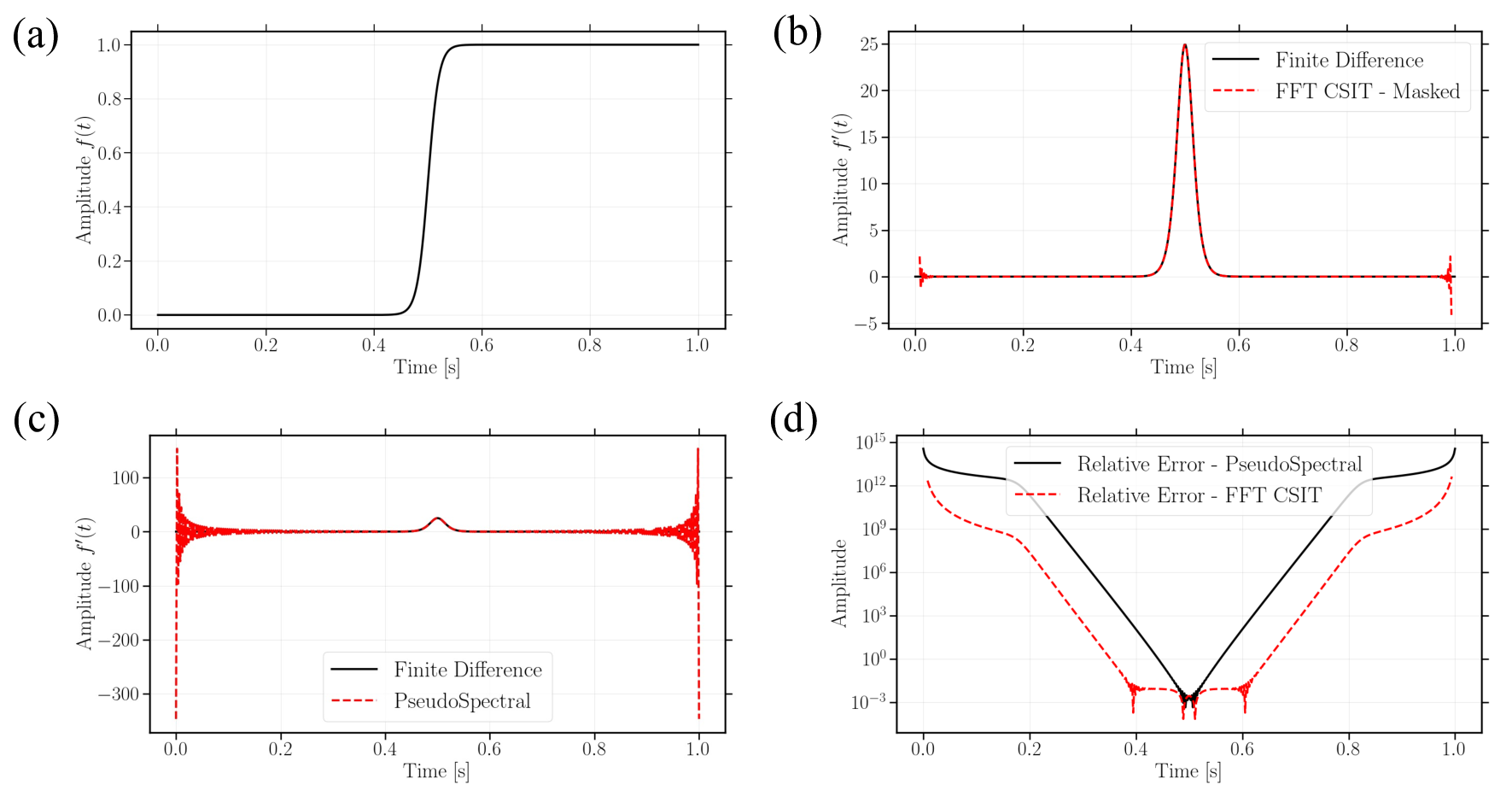
스펙트럼 분석에서는 CSIT가 입력 신호의 푸리에 스펙트럼에 대해 위상은 그대로 유지하면서 진폭을 저주파 영역에서는 거의 변형하지 않고, 고주파 영역에서는 급격히 감쇠시키는 저역통과 필터와 유사한 특성을 보인다. 이는 전통적인 Fourier 미분이 고주파 성분을 증폭시켜 수치 불안정성을 야기하는 문제를 자연스럽게 해결한다는 의미이다. 또한 실수 스텝(δ)과 허수 스텝(ε)의 비율을 조절함으로써 평활화 강도와 미분 정확도 사이의 트레이드오프를 사용자가 직접 제어할 수 있다.
구현 측면에서 저자는 두 가지 접근법을 제시한다. 첫 번째는 FFT를 이용한 전역 변환으로, 대규모 주기적 데이터에 대해 O(N log N)의 계산 복잡도를 유지한다. 두 번째는 고차 보간(interpolation) 기반 로컬 변환으로, 비주기적 경계 조건이나 불규칙한 격자에서도 적용 가능하도록 설계되었다. 특히 보간 기반 구현은 지역적인 스텝 크기 조절이 가능해, 급격한 신호 변동이 있는 구간에서 적응형 ε 값을 적용함으로써 과도한 평활화를 방지한다.
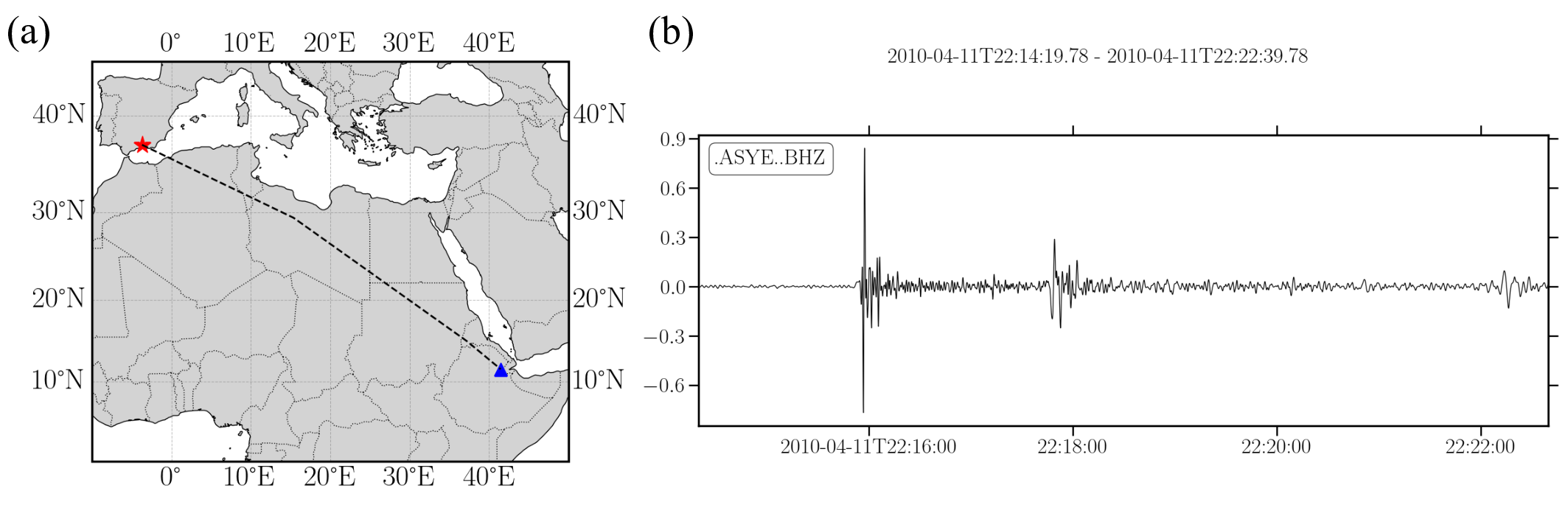
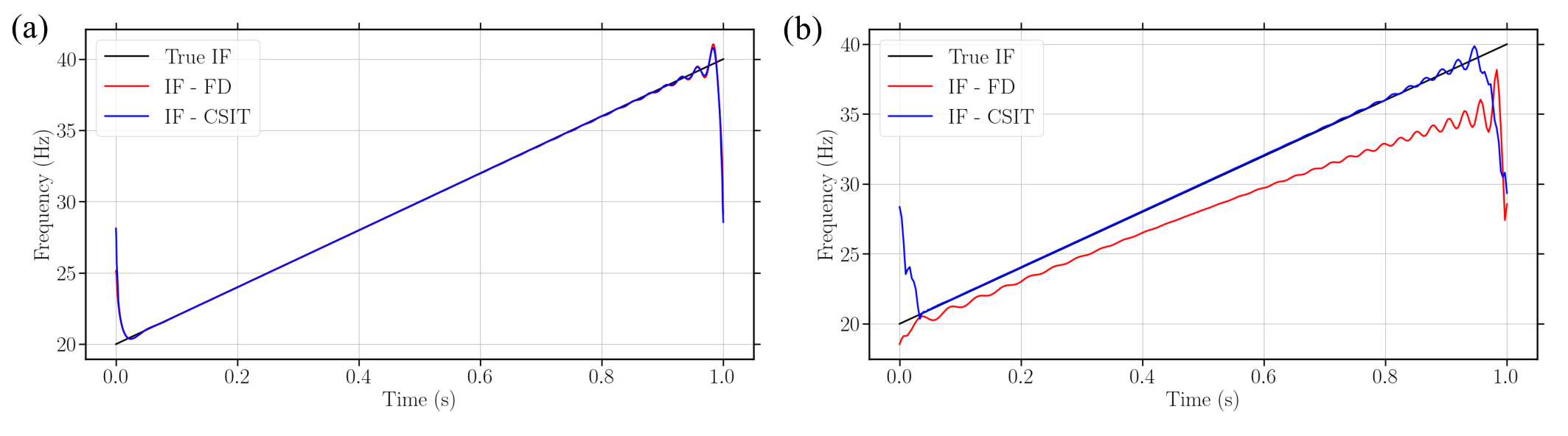
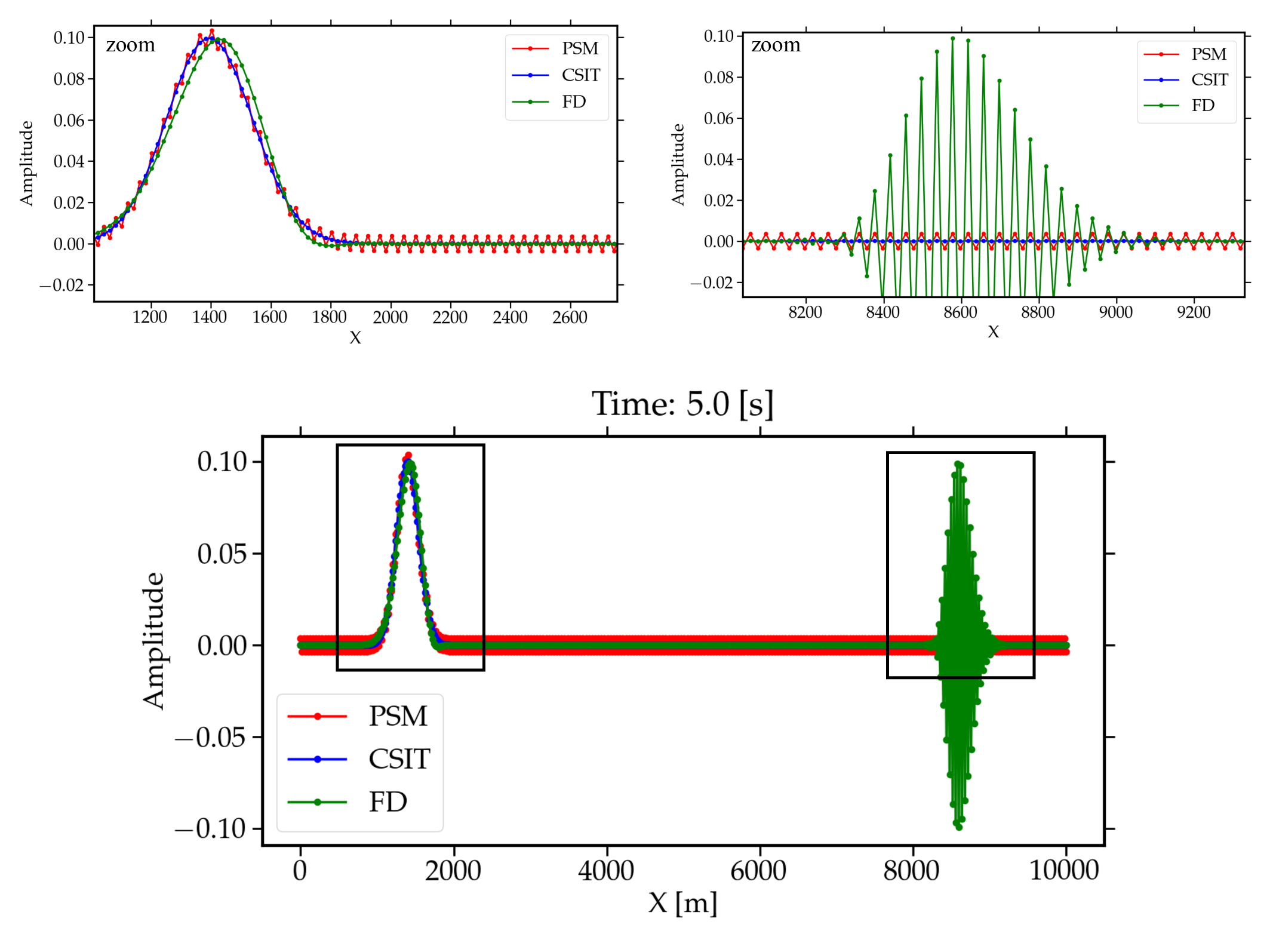
응용 사례로는 1차 대류 방정식의 수치 해석과 순간 주파수(instantaneous frequency) 추정이 제시된다. 대류 방정식에서는 CSIT를 미분 연산에 삽입함으로써 수치 확산(diffusion) 효과가 감소하고, 시간 전진 단계에서 발생할 수 있는 고주파 진동이 억제되어 보다 안정적인 솔루션을 얻었다. 순간 주파수 계산에서는 Hilbert 변환 기반의 아날리시스와 비교했을 때, 위상 왜곡이 현저히 감소하고, 잡음에 대한 민감도가 낮아 실제 지진 데이터와 같은 비정상 신호에서도 신뢰할 수 있는 결과를 제공한다.
마지막으로 향후 연구 방향으로는 (1) 비주기적 경계 조건을 직접 다루는 변환 커널 설계, (2) 신호 특성에 따라 자동으로 δ와 ε를 최적화하는 머신러닝 기반 파라미터 튜닝, (3) 고차 유한요소(FEM)와 결합하여 국부적인 미분 연산을 강화하는 하이브리드 프레임워크 구축 등이 제시된다. 이러한 확장은 CSIT를 단순한 수치 미분 도구를 넘어, 복합 물리 현상 시뮬레이션, 지진 탐사, 의료 영상 등 다양한 분야에 적용 가능한 범용 신호 처리 플랫폼으로 발전시킬 잠재력을 보여준다.
📄 논문 본문 발췌 (Excerpt)
📸 추가 이미지 갤러리