반분리 쌍 분해의 최적 구성과 저차원 스패너 응용
📝 원문 정보
- Title: New Constructions of SSPDs and their Applications
- ArXiv ID: 2512.08619
- 발행일: 2025-12-09
- 저자: Mohammad A. Abam, Sariel Har-Peled
📝 초록 (Abstract)
** 우리는 ℝ^d에 있는 n개의 점 집합에 대해 새로운 최적의 반분리 쌍 분해(SSPD)를 제시한다. 새로운 구성에서는 각 점이 소수의 쌍에만 참여하며, 저차원(낮은 배율 차원) 공간에도 쉽게 확장된다. 이는 이러한 특성을 동시에 만족하는 최초의 최적 구성이다. 이를 활용하여 고정된 t > 1에 대해 O(n)개의 간선과 최대 차수 O(log² n)를 갖는 t‑스패너를 구축하고, 이 스패너는 크기 O(n^{1‑1/d})인 분리자를 가진다.**
💡 논문 핵심 해설 (Deep Analysis)
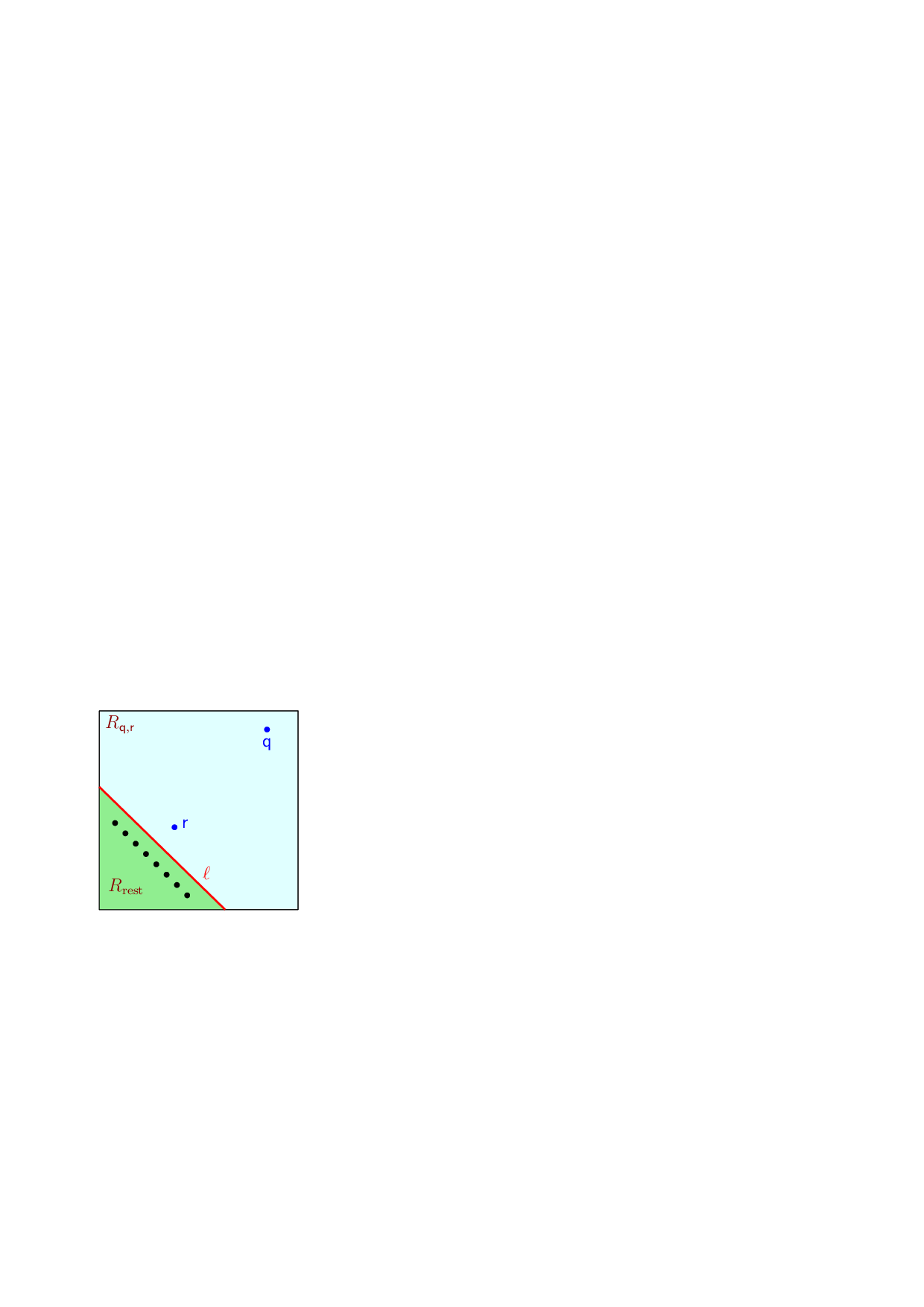
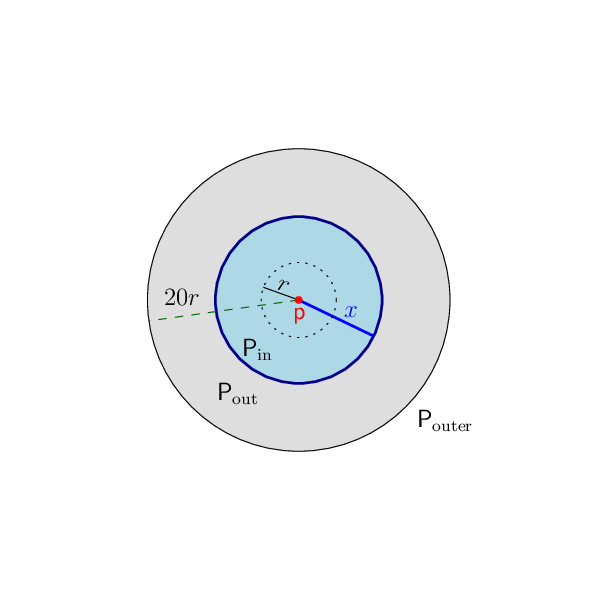
반분리 쌍 분해(SSPD)는 거리 기반 알고리즘, 특히 근접 탐색, 범위 검색 및 그래프 스파닝에 핵심적인 전처리 구조이다. 기존의 SSPD 구현은 보통 각 점이 O(log n)개의 쌍에 포함되는 형태였으며, 차원 d가 증가함에 따라 복잡도가 급격히 악화되는 문제가 있었다. 본 논문은 “각 점이 몇 개의 쌍에만 참여한다”는 강력한 희소성 조건을 만족하면서도 전체 쌍의 개수를 Θ(n) 수준으로 유지하는 최적 구성을 제시한다. 이는 특히 배율 차원(doubling dimension)이 낮은 메트릭 공간—예를 들어, 저차원 유클리드 공간이나 저차원 매니폴드—에서 효율적인 구현이 가능함을 의미한다.
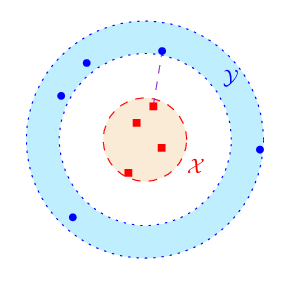
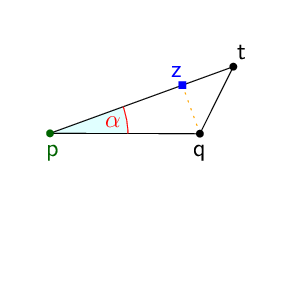
기술적인 핵심은 점들을 계층적 클러스터링 구조에 배치하고, 각 클러스터 간의 거리 관계를 정교하게 조절함으로써 불필요한 쌍을 제거하는 방법이다. 이 과정에서 사용되는 “반분리” 조건은 두 클러스터가 서로 충분히 멀리 떨어져 있으면 하나의 쌍으로 대체할 수 있다는 아이디어에 기반한다. 결과적으로, 각 점은 자신의 클러스터와 인접 클러스터 사이에서 제한된 수의 파트너만을 갖게 되며, 전체 쌍의 수는 O(n)으로 제한된다.
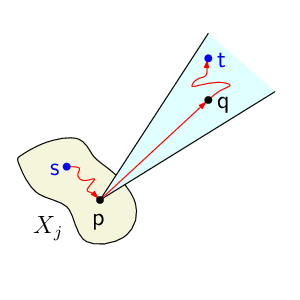
이러한 SSPD를 기반으로 만든 t‑스패너는 두드러진 두 가지 장점을 가진다. 첫째, 간선 수가 O(n)으로 선형이며, 이는 대규모 데이터셋에서도 메모리와 연산 비용을 크게 절감한다. 둘째, 최대 차수가 O(log² n)으로 제한되어 있어, 네트워크 라우팅이나 분산 시스템에서 발생할 수 있는 병목 현상을 최소화한다. 특히, 스패너가 O(n^{1‑1/d}) 크기의 분리자를 갖는다는 점은 그래프 분할 알고리즘이나 병렬 처리 시에 균형 잡힌 파티션을 손쉽게 얻을 수 있음을 시사한다.
이 연구는 기존의 SSPD와 스패너 설계에서 나타났던 차원 저주와 복잡도 상한을 동시에 극복한 최초의 결과라 할 수 있다. 실용적인 측면에서는 지리 정보 시스템, 로봇 경로 계획, 그리고 고차원 데이터 분석에서 거리 기반 구조를 필요로 하는 다양한 응용에 바로 적용 가능하다. 다만, 구현 시 클러스터링 단계에서의 상수 팩터와 실제 데이터의 분포에 따라 성능 차이가 발생할 수 있으므로, 향후 연구에서는 경험적 평가와 함께 동적 업데이트를 지원하는 변형을 탐색하는 것이 바람직하다.
**
📄 논문 본문 발췌 (Excerpt)
📸 추가 이미지 갤러리