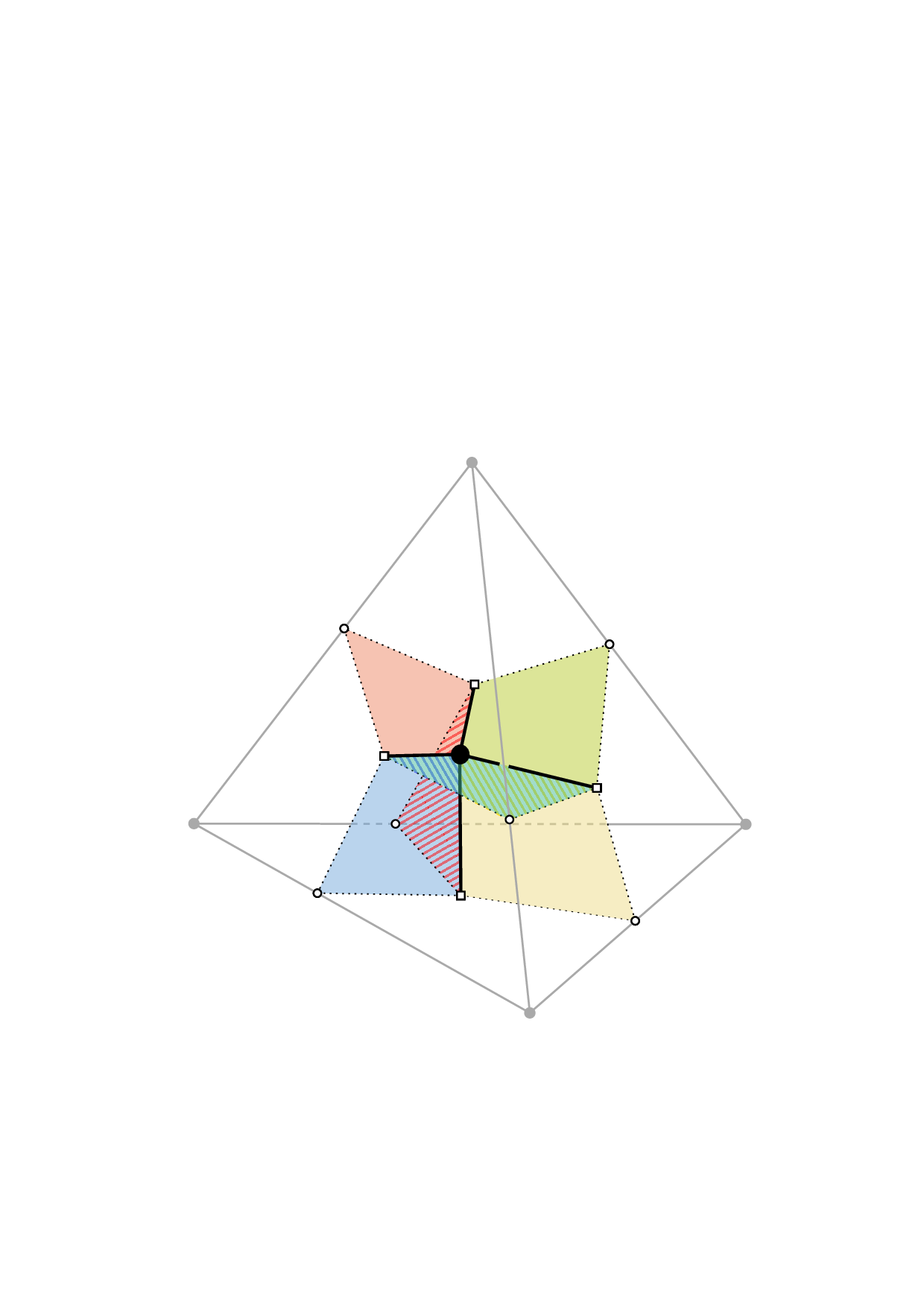트리폭을 보존한 3‑다양체 삼각분할의 변환과 퀀텀 불변량의 고정‑파라미터 알고리즘
📝 원문 정보
- Title: On Sparse Representations of 3-Manifolds
- ArXiv ID: 2512.05779
- 발행일: 2025-12-05
- 저자: Kristóf Huszár, Clément Maria
📝 초록 (Abstract)
** 3‑다양체는 보통 추상적인 사면체들의 삼각분할로 표현되며, 그 삼각형 면들은 쌍으로 식별된다. 삼각분할의 조합적 희소성은 이중 그래프의 트리폭으로 측정되며, 이는 파라미터화된 알고리즘 설계에 핵심적인 역할을 한다. 본 연구에서는 특정 희소성 파라미터를 제어하면서 주어진 삼각분할을 변형하거나 수정하는 알고리즘 절차를 조사한다. 첫째, 주어진 삼각분할을 해당 3‑다양체의 히어로드 도표로 변환하는 선형 시간 알고리즘을 제시하고, 이 변환이 트리폭을 보존함을 보인다. 이 구성을 이용해 Kuperberg의 3‑다양체 양자 불변량을 계산하기 위한 고정‑파라미터 가능한 프레임워크를 제시한다. 둘째, 주어진 삼각분할을 최대 가장자리 밸런스가 9 이하가 되도록 재삼각분할하는 거의 선형 시간 알고리즘을 제시하되, 이 과정에서 이중 그래프의 트리폭이 크게 증가하지 않음을 보인다. 이 두 알고리즘을 결합하면, 주어진 삼각분할로부터 모든 부착 곡선이 최대 9개의 다른 곡선과만 교차하는 히어로드 도표를 거의 선형 시간에 생성할 수 있다.**
💡 논문 핵심 해설 (Deep Analysis)
이 논문은 3‑다양체 위상학에서 가장 실용적인 데이터 구조인 삼각분할을 다루면서, 그래프 이론의 핵심 개념인 트리폭을 중심으로 알고리즘적 효율성을 극대화한다는 점에서 큰 의미를 가진다. 트리폭은 그래프가 트리와 얼마나 유사한지를 정량화하는 파라미터이며, 트리폭이 작을수록 동적 계획법이나 색칠 알고리즘 같은 전통적인 FPT 기법을 적용하기 용이하다. 기존 연구에서는 삼각분할 자체의 트리폭을 이용해 다양한 위상학적 문제(예: 매니폴드 동형판별, 코흐라 복합체 계산 등)를 FPT로 해결했지만, 히어로드 분할이라는 전혀 다른 표현으로 변환하면서도 트리폭을 보존한다는 사실은 새로운 전환점이다.
첫 번째 알고리즘은 삼각분할을 히어로드 도표로 변환하는 과정에서, 사면체의 면 식별 정보를 이용해 두 개의 손잡이(핸들바디)와 그 사이의 부착곡선을 구성한다. 이때 이중 그래프의 정점은 사면체, 간선은 면 식별을 나타내며, 변환 과정은 각 사면체를 손잡이의 한 부분으로 매핑하고 부착곡선을 따라 연결함으로써 트리폭이 그대로 유지된다. 선형 시간 복잡도는 입력 삼각분할의 크기(사면체 수)에 비례하므로, 대규모 데이터에도 실용적이다.
이 변환을 활용해 Kuperberg의 양자 불변량을 계산하는 프레임워크를 제시한다는 점은 특히 주목할 만하다. Kuperberg 불변량은 텐서 네트워크와 관련된 복잡한 다항식이며, 일반적으로 지수적 시간 복잡도를 가진다. 그러나 트리폭이 제한된 히어로드 도표에서는 텐서 네트워크를 트리 구조에 맞게 분해해 동적 계획법으로 효율적으로 평가할 수 있다. 따라서 “트리폭 + 히어로드 변환”이라는 두 단계가 결합되어, 양자 불변량 계산을 고정‑파라미터 가능한(FPT) 문제로 전환한다.
두 번째 알고리즘은 삼각분할의 가장자리 밸런스(한 가장자리에 부착된 사면체 수)를 9 이하로 제한한다. 이는 기존 삼각분할에서 발생할 수 있는 높은 밸런스가 알고리즘의 메모리와 시간 복잡도를 급격히 악화시키는 문제를 완화한다. 저자들은 quasi‑linear 시간(즉, O(n log k) 수준) 안에 재삼각분할을 수행하면서, 트리폭이 과도하게 증가하지 않도록 세심한 지역적 교체와 스플리팅 기법을 적용한다. 결과적으로, 변환 후의 히어로드 도표에서 각 부착곡선이 교차하는 곡선 수가 최대 9개로 제한되어, 곡선 교차 그래프의 밀도가 낮아지고, 이는 다시 텐서 네트워크 평가 단계에서 연산량을 크게 감소시킨다.
이 두 절차를 연쇄적으로 적용하면, 입력 삼각분할을 거의 선형 시간에 “트리폭 보존 + 낮은 가장자리 밸런스 + 제한된 곡선 교차”라는 세 가지 희소성 조건을 만족하는 히어로드 도표로 변환할 수 있다. 이는 3‑다양체 위상학의 계산적 연구뿐 아니라, 양자 컴퓨팅, 텐서 네트워크 시뮬레이션, 그리고 복잡한 위상적 데이터의 효율적 저장·전송에 직접적인 응용 가능성을 제공한다. 특히, 트리폭을 핵심 파라미터로 삼는 FPT 접근법이 실제 구현(예: Regina 소프트웨어)에서도 성공적으로 적용된 점은 이론과 실무가 잘 결합된 사례라 할 수 있다.
**
📄 논문 본문 발췌 (Excerpt)
📸 추가 이미지 갤러리