다항식 신경 전단 사프 신경망 스펙트럼 기반 이질성 그래프 학습 혁신
📝 원문 정보
- Title: Polynomial Neural Sheaf Diffusion: A Spectral Filtering Approach on Cellular Sheaves
- ArXiv ID: 2512.00242
- 발행일: 2025-11-28
- 저자: Alessio Borgi, Fabrizio Silvestri, Pietro Liò
📝 초록 (Abstract)
Sheaf Neural Network(SheafNN)는 그래프의 각 정점에 로컬 벡터 공간을 부여하고 학습 가능한 전송 맵을 통해 이질성 및 과평활 현상에 대한 원리적인 편향을 제공한다. 기존 Neural Sheaf Diffusion(NSD)은 SVD 기반 정규화와 조밀한 엣지 제한 맵에 크게 의존하는 공간적 접근으로, 연산과 최적화가 불안정하고 스토크 차원에 강하게 결합된다. 본 연구는 스펙트럼 영역에서 확산을 명시적으로 수행하는 Polynomial Neural Sheaf Diffusion(PolyNSD)을 제안한다. PolyNSD는 정규화된 Sheaf Laplacian의 차수‑K 다항식으로 전파를 모델링하며, 스펙트럼 재스케일링된 연산자에 대한 안정적인 3항 재귀를 통해 구현한다. 이를 통해 단일 레이어에서 명시적인 K‑hop 수용 영역을 제공하고, 직교 다항식 필터의 볼록 조합으로 직접 학습 가능한 스펙트럼 응답을 얻는다. 또한 PolySpectralGNN이라는 비‑Sheaf 베이스라인을 도입해 PolyNSD와 동일한 스펙트럼 연산자를 사용한다. 동질·이질성 벤치마크 전반에 걸쳐 PolyNSD는 최첨단 성능을 달성하면서, 대각 제한 맵만으로도 정확도가 큰 스토크 차원에 의존하지 않음을 입증한다. 결과적으로 실행 시간과 메모리 사용량이 크게 감소한다. 우리는 다항식 계열, 이질성 수준, 연속 영역 확장, 과평활 진단, 장거리 영향 감소를 통한 과압축 탐색, 스펙트럼 해석 분석 등을 통해 PolyNSD를 종합적으로 검증한다.💡 논문 핵심 해설 (Deep Analysis)
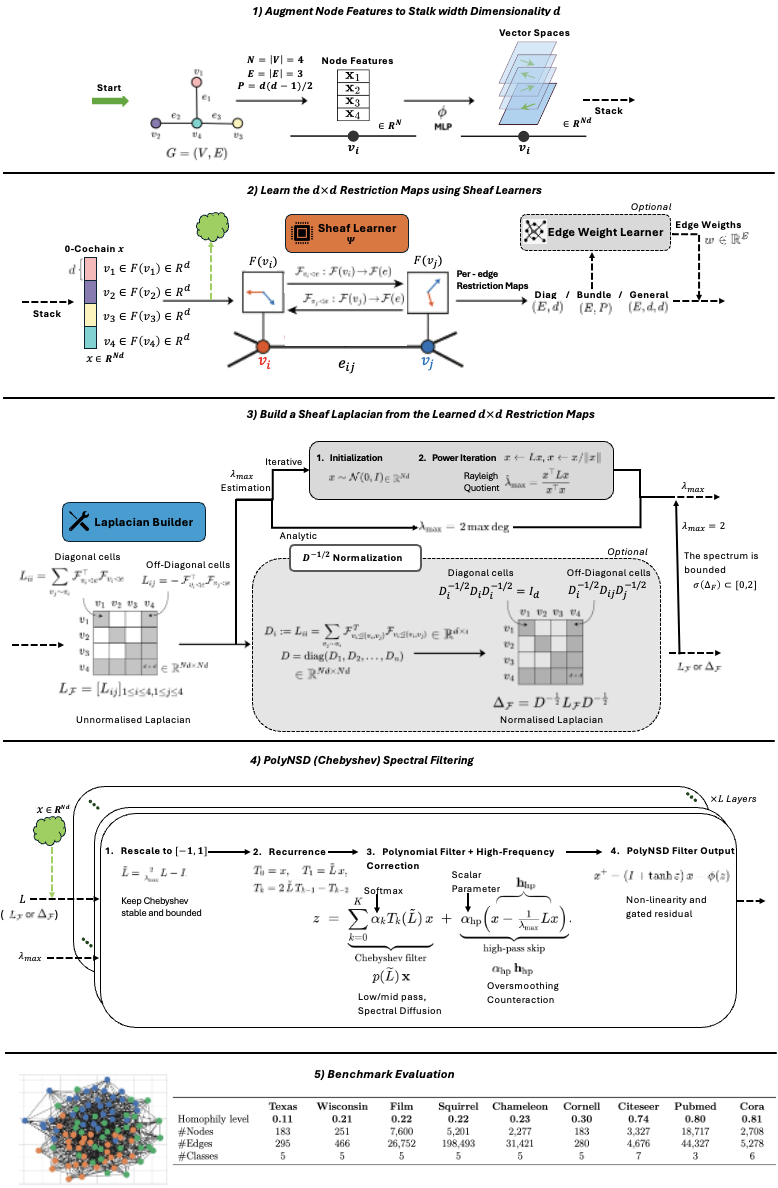
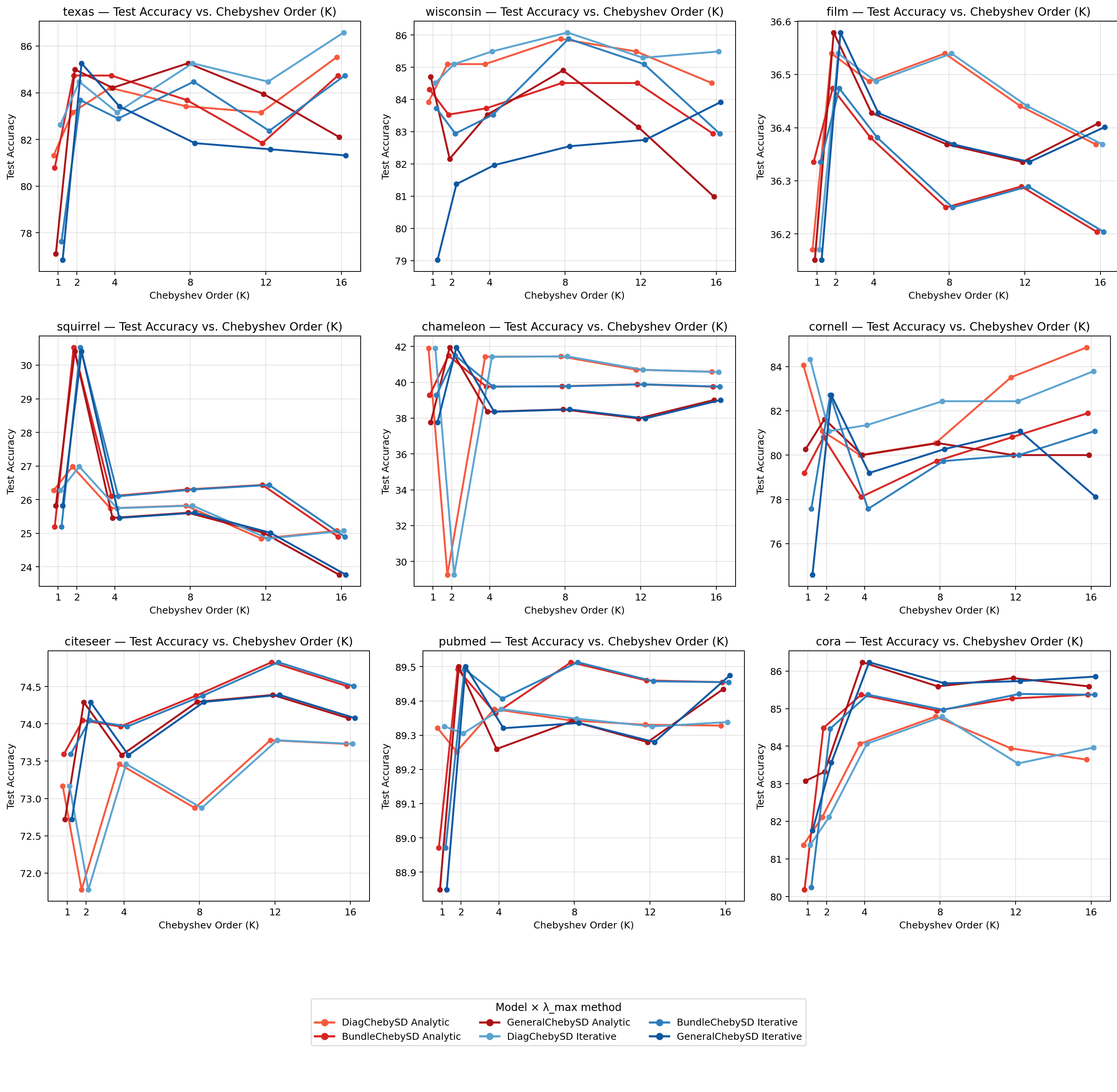
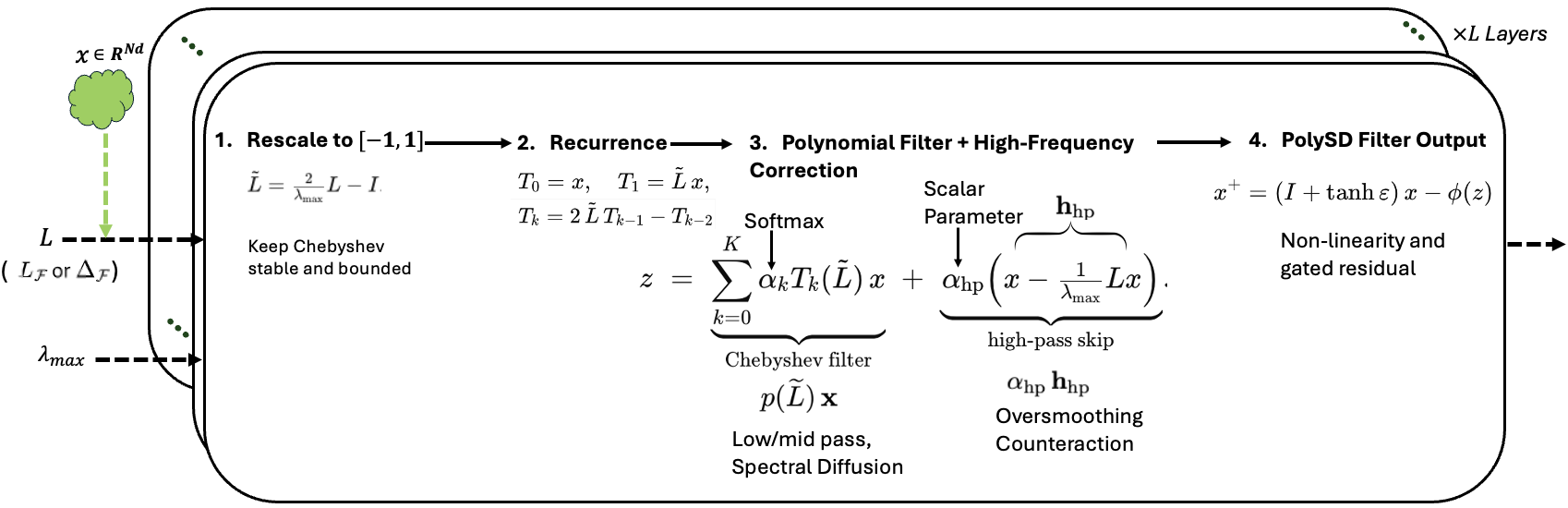
PolyNSD는 이러한 구조적 한계를 스펙트럼 영역으로 옮겨 해결한다. 핵심 아이디어는 정규화된 Sheaf Laplacian L̂을 스펙트럼적으로 재스케일링한 뒤, 차수 K의 다항식 p_K(L̂)=∑{k=0}^{K}α_k T_k(L̂) 형태로 확산 연산을 정의하는 것이다. 여기서 T_k는 Chebyshev 다항식(또는 다른 직교 다항식)이며, 3항 재귀 T{k+1}=2L̂ T_k - T_{k-1}를 이용해 O(K·|E|)의 선형 복잡도로 계산된다. 이 접근법은 다음과 같은 장점을 제공한다.
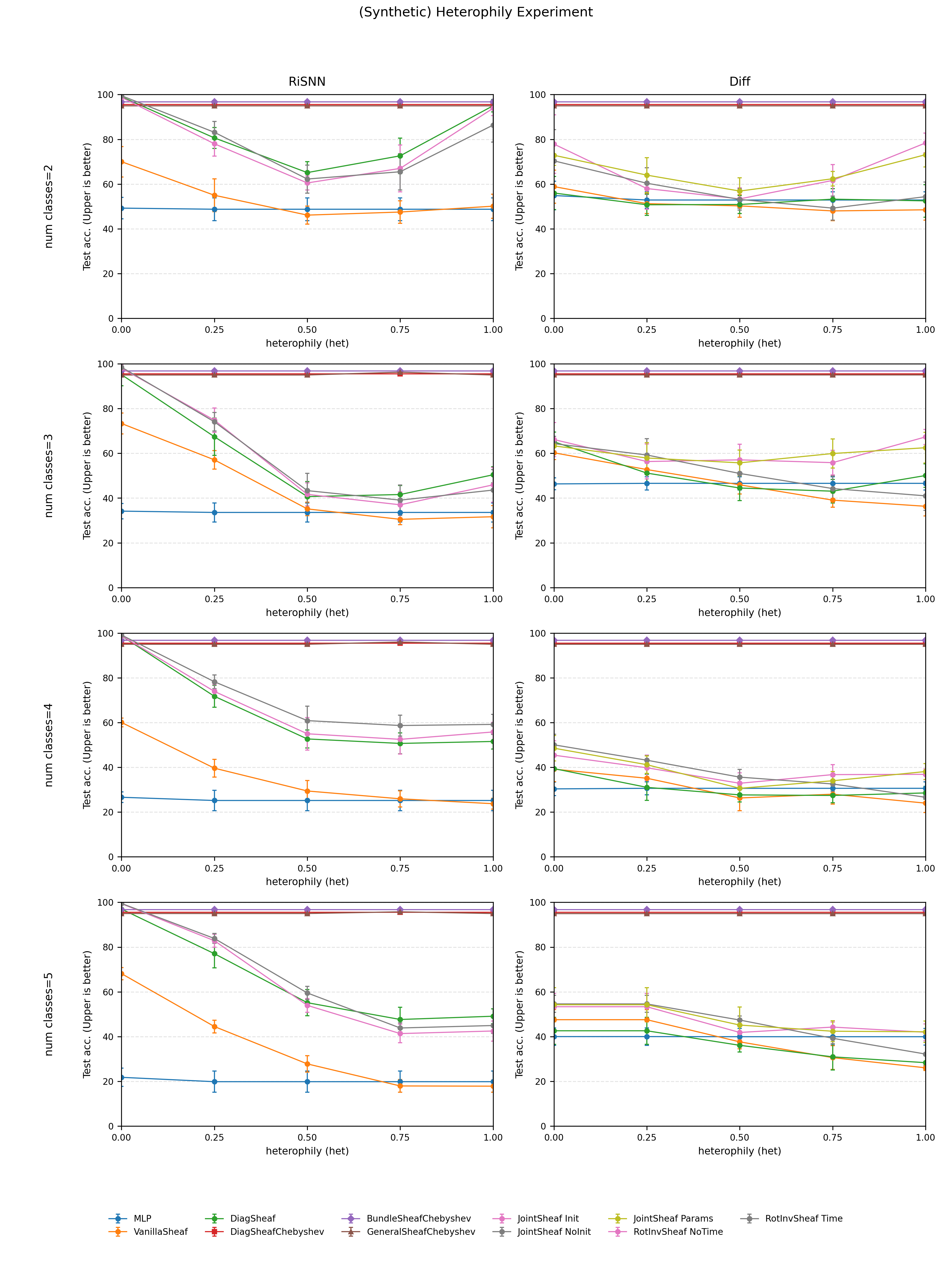
명시적 K‑hop 수용 영역: 다항식 차수가 바로 전파 깊이를 결정하므로, 하나의 레이어에서 K단계 이웃 정보를 동시에 통합한다. 이는 기존 NSD가 여러 레이어를 쌓아야 구현하던 장기 의존성을 단일 연산으로 압축한다.
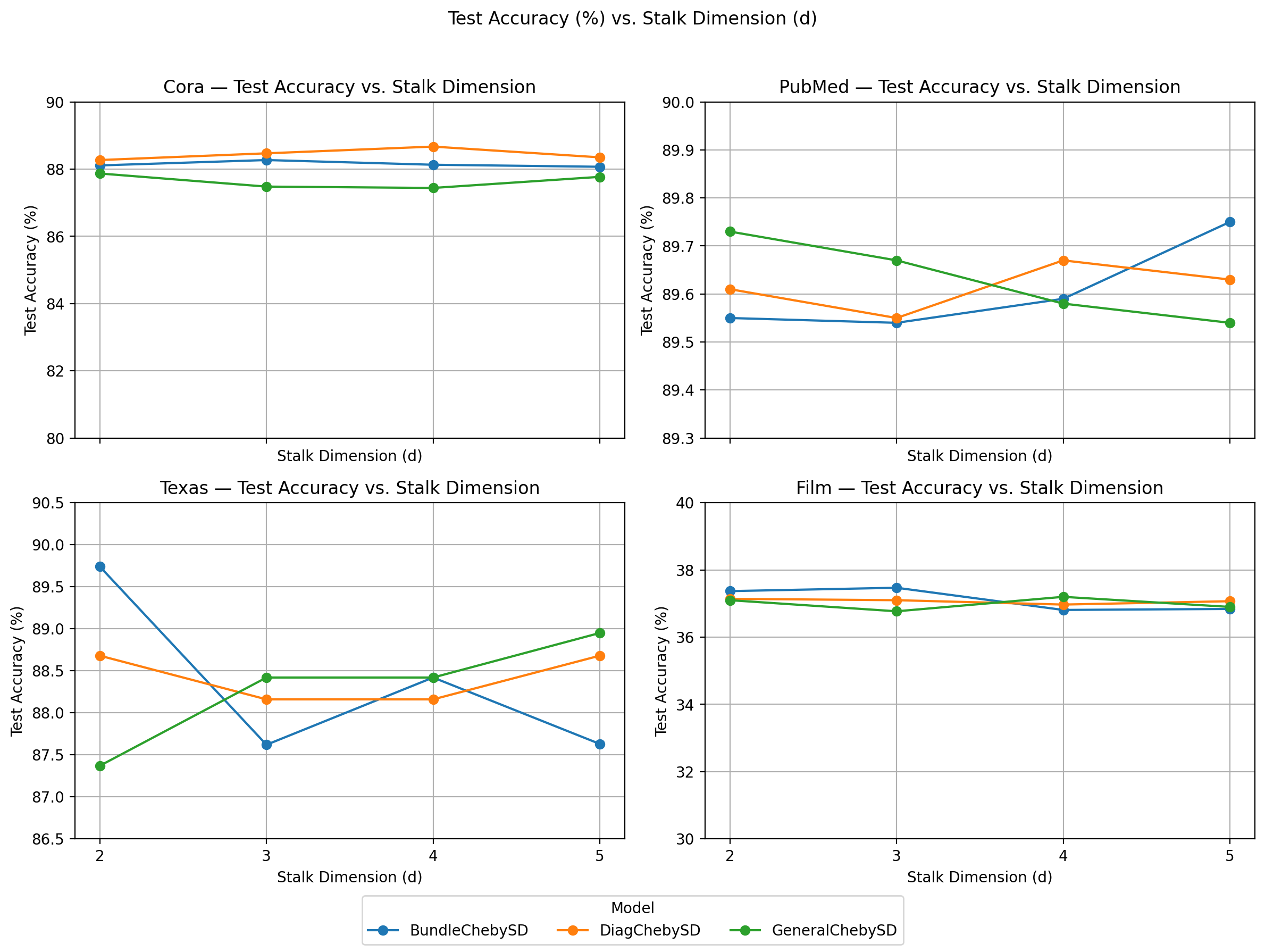
파라미터 효율성: 전송 맵은 이제 대각 행렬(스칼라 스케일링)만을 학습하거나, 필요에 따라 소수의 저차원 매개변수(α_k)만을 최적화한다. 따라서 파라미터 수는 O(K) 수준으로 감소하고, 스토크 차원 d와 무관하게 정확도가 유지된다.
스펙트럼 해석 가능성: α_k는 다항식 필터의 스펙트럼 응답을 직접 조절한다. 학습 과정에서 얻어지는 α_k 값들을 분석하면, 모델이 어떤 고유값 범위에 주목하는지 시각화할 수 있어, 이질성 그래프에서 저주파(동질성)와 고주파(이질성) 신호를 어떻게 균형 잡는지 직관적으로 파악한다.
안정성 및 확장성: 3항 재귀는 수치적으로 매우 안정적이며, 스펙트럼 재스케일링(λ∈
📄 논문 본문 발췌 (Excerpt)
📸 추가 이미지 갤러리