회전 중성자 별 주변의 새로운 자기권 모델

📝 원문 정보

• Title: Pulsar Magnetosphere
• ArXiv ID: 1101.3100
• 발행일: 2011-01-18
• 저자: Andrei Gruzinov

📝 초록 (Abstract)

: 이 논문은 빠르게 회전하는 자기화된 전도 구가 진공에서 어떻게 자기권을 형성하는지에 대한 새로운 시뮬레이션 결과를 제시한다. 이 연구는 중성자 별의 자기권 형성을 설명하며, 특히 펄사의 방출 현상을 이해하는데 중요한 역할을 한다. 기존 모델에서는 축대칭 펄사의 경우 빛 원통 바깥에서 특이 전류층이 형성되며 이로 인해 포팅 플럭스(Poynting flux)가 감소하는 것으로 나타났다. 본 논문은 이러한 현상을 정확하게 시뮬레이션하고, 이를 통해 기존의 계산 결과를 개선한다.

💡 논문 핵심 해설 (Deep Analysis)

: 이 논문은 중성자 별 주변의 자기권 형성을 이해하는데 있어 중요한 이론적 접근법을 제시한다. 특히, 회전하는 전도 구가 진공에서 어떻게 자기권을 형성하는지에 대한 새로운 시뮬레이션 결과를 통해 기존 모델의 한계를 극복하고자 한다.

1. 이론적 배경

• Schwinger Field와 양자 전자 역학(QED) 과정: 이 논문은 회전하는 자기화된 전도 구가 진공에서 전하를 생성하는 메커니즘을 설명한다. 이는 Schwinger field에 도달하기 전의 1차 수준 QED 과정이나 표면에서 전하 입자를 끌어당기는 현상으로 인해 발생할 수 있다.
• Pulsar Magnetosphere: 중성자 별 주변의 자기권은 Goldreich와 Julian (1969)에 의해 처음 제시되었으며, 이후 Contopoulos, Kazanas 및 Fendt (1999), Gruzinov (2005), Spitkovsky (2006) 등 여러 연구자들에 의해 발전되었다. 그러나 이 논문은 이러한 기존 모델의 한계를 지적하며 새로운 접근법을 제시한다.

2. 기존 모델의 문제점

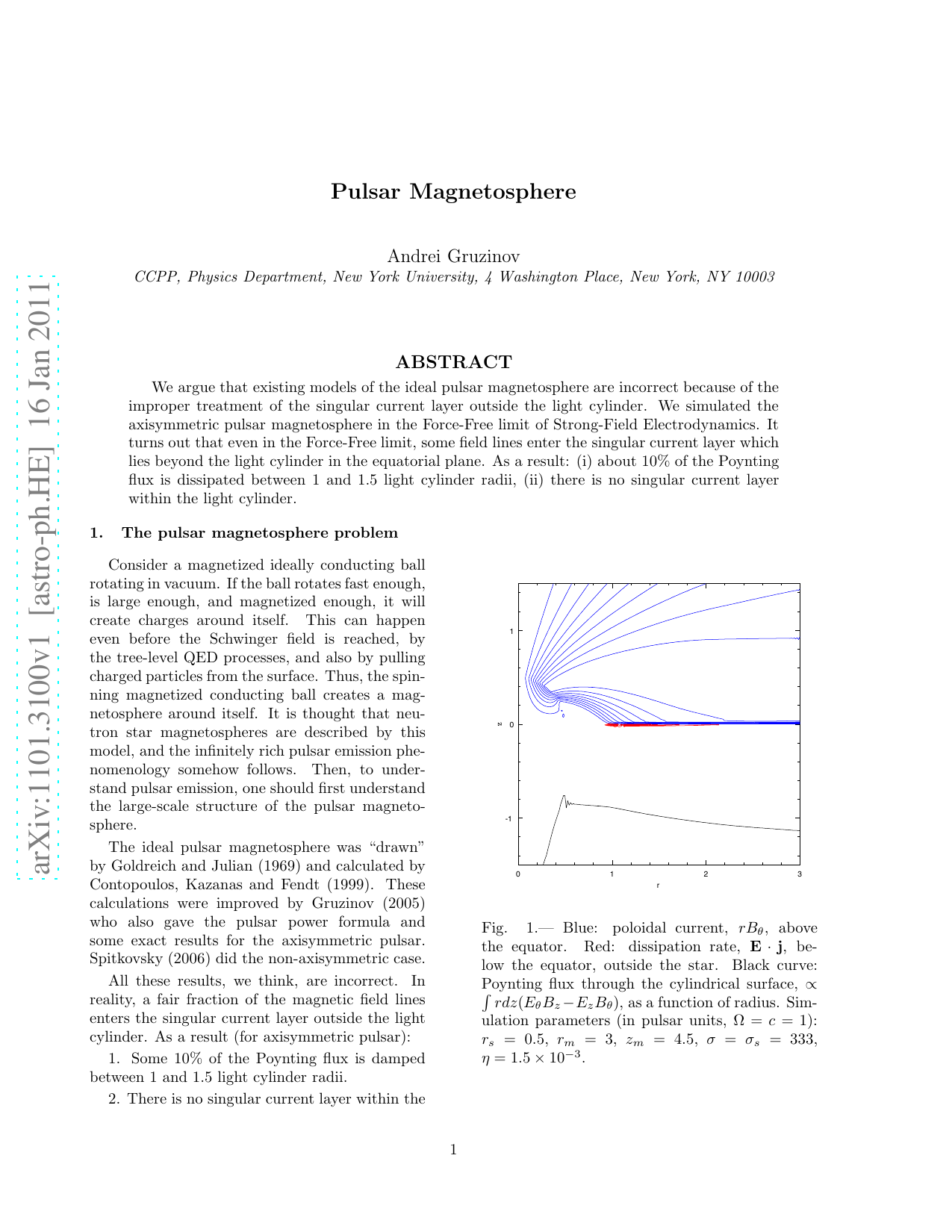
• 축대칭 펄사와 빛 원통 바깥의 특이 전류층: 기존 연구에서는 축대칭 펄사의 경우, 빛 원통 바깥에서 특이 전류층이 형성되며 이로 인해 포팅 플럭스(Poynting flux)가 약 10% 감소하는 것으로 나타났다. 그러나 이러한 결과는 빛 원통 바깥의 특이 전류층을 부적절하게 처리한 데서 기인한다.
• 경계 조건의 문제: 이전 연구에서는 경계 조건을 사용하여 시뮬레이션을 수행하였으나, 본 논문은 이러한 접근법을 개선하고자 한다.

3. 새로운 모델과 시뮬레이션

• Strong-Field Electrodynamics (SFE)와 Force-Free Electrodynamics (FFE): 이 논문에서는 SFE와 FFE를 사용하여 중성자 별 주변의 자기권을 시뮬레이션한다. 특히, SFE는 전도성이 높은 한계에서 FFE로 수렴하며, 이는 전기장과 자기장이 항상 평행하게 배치되는 경우에 해당한다.
• 수치적 방법: 논문에서는 3+1 분할을 사용하여 방정식을 해결하고, SFE와 FFE의 오엄의 법칙을 적용한다. 특히, SFE는 전기장과 자기장이 항상 평행하게 배치되는 경우에 해당하며, 이는 빛 원통 바깥에서 특이 전류층을 정확하게 처리할 수 있게 한다.
• 시뮬레이션 결과: 시뮬레이션은 공간 해상도와 전도성 σ 및 σ_s를 증가시키고 확산성 η을 감소시키면서 수행되었다. 이러한 변화는 별 외부의 최종 자기권에서 명확한 포화 징후가 나타날 때까지 지속되었으며, 이를 통해 기존 모델과 다른 형태의 자기권이 형성되는 것을 확인할 수 있었다.

4. 결론

본 논문은 중성자 별 주변의 자기권 형성을 이해하는데 있어 중요한 이론적 접근법을 제시한다. 특히, 회전하는 전도 구가 진공에서 어떻게 자기권을 형성하는지에 대한 새로운 시뮬레이션 결과를 통해 기존 모델의 한계를 극복하고자 한다. 이러한 연구는 펄사의 방출 현상을 이해하는데 중요한 역할을 하며, 앞으로 중성자 별 주변의 자기권 형성을 더욱 정확하게 예측하는 데 도움이 될 것으로 보인다.

이 논문은 기존 모델에서 간과되었던 빛 원통 바깥의 특이 전류층에 대한 새로운 이해를 제공하며, 이를 통해 중성자 별 주변의 자기권 형성을 더욱 정확하게 예측할 수 있는 길을 열었다. 이러한 연구는 향후 중성자 별과 펄사의 방출 현상을 이해하는데 중요한 기여를 할 것으로 보인다.

📄 논문 본문 발췌 (Excerpt)

📸 추가 이미지 갤러리

Reference