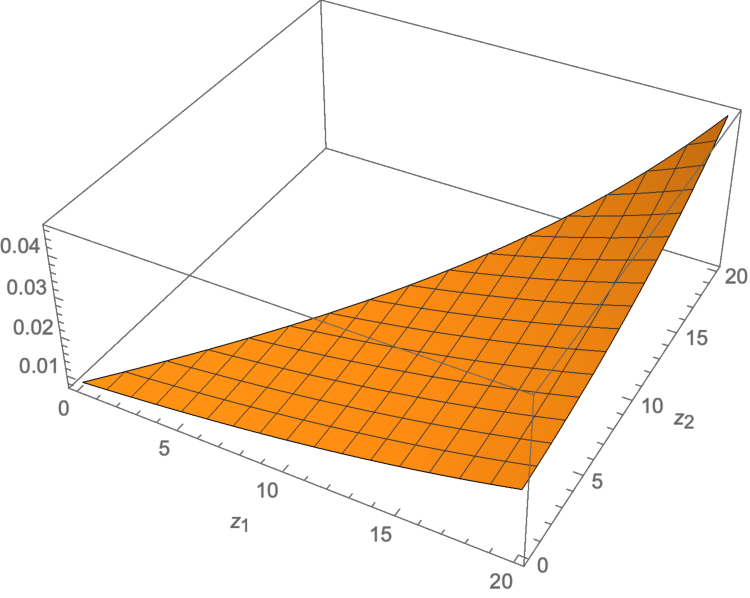
다변량 무작위 변수의 암시적 커플라 표현: 푸리에 방법을 통한 계산
이 논문은 다차원 랜덤 변수의 암시적 커플라 표현에 대한 새로운 접근법을 제안하며, 특히 푸리에 방법을 활용한 계산 기법을 소개한다. 이 연구는 무작위 변수 간의 의존성 구조를 효과적으로 묘사하는 데 중점을 두고 있으며, 이를 통해 동적 과정에서 발생하는 복잡한 상호 작용을 이해하고 분석할 수 있는 도구를 제공한다. 1. 커플라와 의존성 구조 커플라는 무작위 변수 간의 의존성을 완벽하게 묘사하며, 스클라르의 정리를 통해 공동 분포와 이분 분포 사이의 관계를 우아하게 연결한다. 그러나 커플라는 동적 과정과 잘 어울리지 않으며, 예를