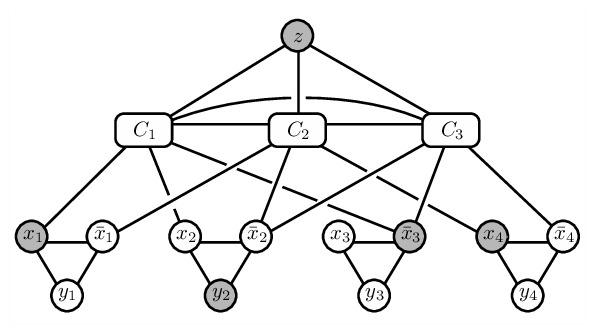
트리 너비를 통한 노드 가드담 유형 정리: 그래프 이론에서의 응용
: 본 연구에서는 노드 가드담 유형 정리를 사용하여 트리 너비(treewidth)에 대한 새로운 관점을 제시하고 있습니다. 이는 특히 그래프 이론에서 중요한 매개변수로, 그래프의 복잡성을 측정하는 데 활용됩니다. 트리 너비와 그 의미: 트리 너비는 그래프 G를 부분 그래프로 포함할 수 있는 k 트리(k tree)의 최소 정수 k를 나타냅니다. 이는 트리 분해(tree decomposition)를 통해 정의되며, 그래프의 복잡성을 측정하는 데 중요한 역할을 합니다. 노드 가드담 유형 정리와 트리 너비: 본 논문에서 제시된 노드 가드담